华师版七年级数学上册-单元清六 期末检测试卷

华师版七年级数学上册-单元清六 期末检测试卷

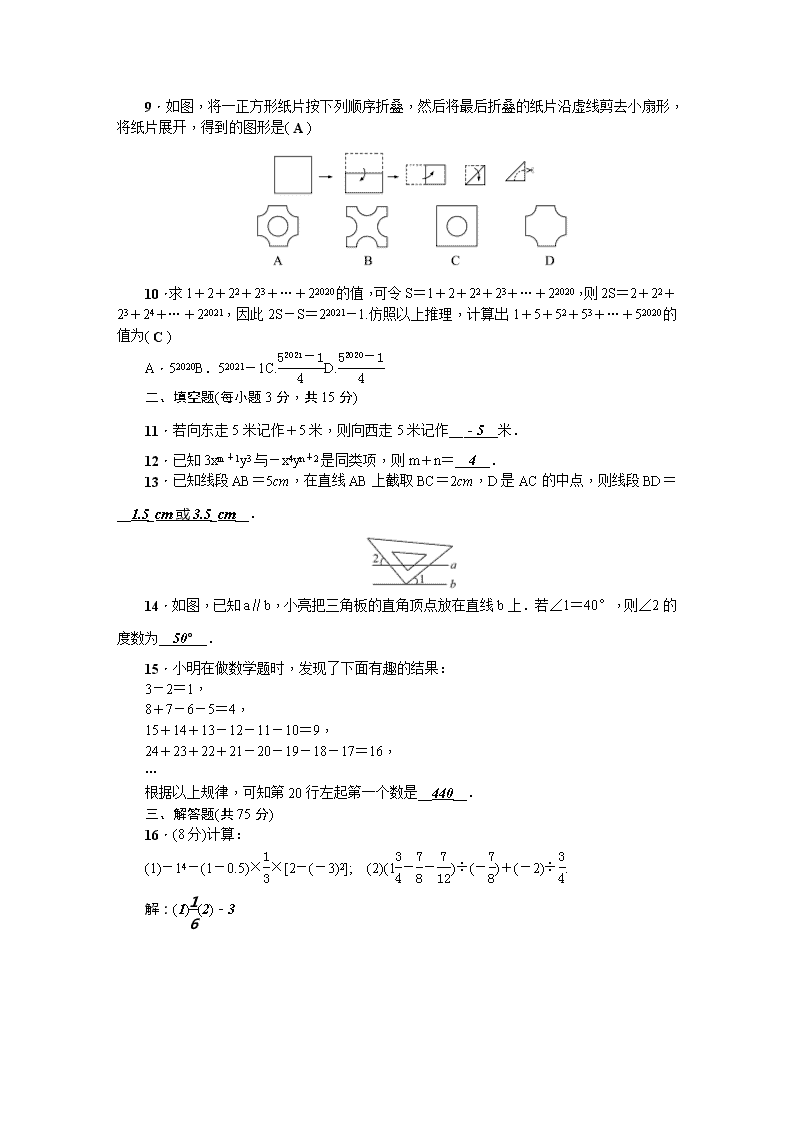
检测内容：期末检测题 得分________卷后分________评价________ 一、选择题(每小题 3 分，共 30 分) 1．(·黔东南州)|－2|的值是( B ) A．－2B．2C．－1 2D.1 2 2．(·北京)如图是某个几何体的展开图，该几何体是( A ) A．三棱柱 B．圆锥 C．四棱柱 D．圆柱 3．(·云南)作为世界文化遗产的长城，其总长大约为 6700000m．将 6700000 用科学记 数法表示为( B) A．6.7×105B．6.7×106C．0.67×107D．67×108 4．下列说法中，正确的个数是( B ) ①任何一个有理数都可以用数轴上的一个点来表示；②数轴上的每一个点都表示一个有 理数；③任何有理数的绝对值都是正数；④每个有理数都有相反数． A．1 个 B．2 个 C．3 个 D．4 个 5．对于任意有理数 a，下列各式不一定成立的是( B ) A．a2＝(－a)2B．a3＝(－a)3C．|a|＝|－a|D．a2≥0 6．如图，数轴的单位长度为 1，如果点 A，B 表示的数的绝对值相等，那么点 A 表示的 数是( B ) A．－4B．－2C．0D．4 7．把一条弯曲的公路改成直道，可以缩短路程，其道理用几何知识解释为( B ) A．两点确定一条直线 B．两点之间，线段最短 C．线段可以比较大小 D．线段有两个端点 8．如图，∠1＋∠2＝180°，可以判断( A ) A．AB∥CDB．AD∥BC C．AD⊥BDD．AB 与 CD 相交 9．如图，将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线剪去小扇形， 将纸片展开，得到的图形是( A ) 10．求 1＋2＋22＋23＋…＋22020 的值，可令 S＝1＋2＋22＋23＋…＋22020，则 2S＝2＋22 ＋23＋24＋…＋22021，因此 2S－S＝22021－1.仿照以上推理，计算出 1＋5＋52＋53＋…＋52020 的值为( C ) A．52020B．52021－1C.52021－1 4 D.52020－1 4 二、填空题(每小题 3 分，共 15 分) 11．若向东走 5 米记作＋5 米，则向西走 5 米记作__－5__米． 12．已知 3xm＋1y3 与－x4yn＋2 是同类项，则 m＋n＝__4__． 13．已知线段 AB＝5cm，在直线 AB 上截取 BC＝2cm，D 是 AC 的中点，则线段 BD＝ __1.5_cm 或 3.5_cm__． 14．如图，已知 a∥b，小亮把三角板的直角顶点放在直线 b 上．若∠1＝40°，则∠2 的度数为__50°__． 15．小明在做数学题时，发现了下面有趣的结果： 3－2＝1， 8＋7－6－5＝4， 15＋14＋13－12－11－10＝9， 24＋23＋22＋21－20－19－18－17＝16， … 根据以上规律，可知第 20 行左起第一个数是__440__． 三、解答题(共 75 分) 16．(8 分)计算： (1)－14－(1－0.5)×1 3 ×[2－(－3)2]; (2)(13 4 －7 8 － 7 12)÷(－7 8)＋(－2)÷3 4. 解：(1)1 6(2)－3 17．(9 分)化简求值： (1)1 2x－3(2x－2 3y2)＋(－3 2x＋y2)，其中 x＝1，y＝2； 解：化简为－7x＋3y2，当 x＝1，y＝2 时，原式＝5 (2)已知 a－b＝2，ab＝－1，求(4a－5b－ab)－(2a－3b＋5ab)的值． 解：化简为 2a－2b－6ab，当 a－b＝2，ab＝－1 时，原式＝10 18．(9 分)由小立方体堆成的某几何体的俯视图如图所示，其中正方形内的数字表示该位 置小方块的个数，请你画出该几何体的主视图和左视图． 解：如图所示： 19．(9 分)某水泥仓库 6 天内进出水泥的吨数如下(“＋”表示进库，“－”表示出库)： ＋20，－25，－13，＋28，－29，－16. (1)经过这 6 天，仓库里的水泥是增多还是减少了？增多或减少了多少吨？ (2)经过这 6 天，仓库管理员结算发现库里还存 200 吨水泥，那么 6 天前，仓库里存有水 泥多少吨？ (3)如果进出仓库的水泥装卸费都是每吨 5 元，那么这 6 天要付多少元装卸费？ 解：(1)＋20＋(－25)＋(－13)＋(＋28)＋(－29)＋(－16)＝20－25－13＋28－29－16＝－ 35(吨)．答：仓库里的水泥减少了，减少了 35 吨 (2)200－(－35)＝235(吨)．答：6 天前，仓 库里存有水泥 235 吨 (3)(|＋20|＋|－25|＋|－13|＋|＋28|＋|－29|＋|－16|)×5＝131×5＝ 655(元)．答：这 6 天要付 655 元的装卸费 20．(9 分)如图，一艘客轮沿东北方向 OC 行驶，在海上 O 处发现灯塔 A 在北偏西 30° 方向上，灯塔 B 在南偏东 60°方向上． (1)在图中画出射线 OA，OB，OC； (2)求∠AOC 与∠BOC 的度数，你发现了什么？ 解：(1)略 (2)∠AOC＝30°＋45°＝75°，∠BOC＝(90°－60°)＋45°＝75°.发现 1： ∠AOC＝∠BOC.发现 2：OC 为∠AOB 的平分线 21．(10 分)如图，直线 AB，CD 相交于点 O，OE⊥CD，OF⊥AB，若∠DOF＝65°， 求∠BOE 和∠AOC 的度数． 解：∵AB⊥OF，CD⊥OE(已知)，∴∠BOF＝∠DOE＝90°(垂直定义)．∵∠DOF＝65°， ∴∠BOD＝90°－65°＝25°，∴∠BOE＝90°－25°＝65°.∴∠AOC＝∠BOD＝25°(对 顶角相等) 22．(10 分)已知：如图，AB∥CD，BD 平分∠ABC，CE 平分∠DCF，∠ACE＝90°. (1)请问 BD 和 CE 是否平行？请你说明理由； (2)AC 和 BD 的位置关系怎样？请说明判断的理由． 解：(1)BD∥CE.理由：∵AB∥CD，∴∠ABC＝∠DCF.∵BD 平分∠ABC，CE 平分∠DCF， ∴∠2＝1 2∠ABC，∠4＝错误!∠DCF，∴∠2＝∠4，∴BD∥CE(同位角相等，两直线平行) (2)AC⊥BD.理由：∵BD∥CE，∴∠DGC＋∠ACE＝180°，∵∠ACE＝90°，∴∠DGC＝ 180°－90°＝90°，即 AC⊥BD 23．(11 分)某单位在五月份准备组织部分员工到成都旅游，现联系了甲、乙两家旅行社， 两家旅行社报价均为 2000 元/人，两家旅行社同时都对 10 人以上的团体推出了优惠举措：甲 旅行社对每位员工七五折优惠；而乙旅行社是免去一位带队管理员工的费用，其余员工八折 优惠． (1)如果设参加旅游的员工共有 a(a>10)人，那么甲旅行社的费用为__1_500a__元，乙旅 行社的费用为__1_600a－1_600__元；(用含 a 的代数式表示，并化简) (2)假如这个单位现组织包括管理员工在内的共 20 名员工到北京旅游，该单位选择哪一 家旅行社比较优惠？请说明理由； (3)如果计划在五月份外出旅游七天，设最中间一天的日期为 a，那么这七天的日期之和 为__7a__；(用含 a 的代数式表示，并化简) (4)假如这七天的日期之和为 63 的倍数，那么他们可能于五月几号出发？(写出所有符合 条件的可能性，并写出简单的计算过程) 解：(2)将 a＝20 代入，得甲旅行社的费用为 1500×20＝30000(元)，乙旅行社的费用为 1600×20－1600＝30400(元)．因为 30000<30400，所以甲旅行社更优惠 (4)①设这七天的日 期和是 63，则 7a＝63，a＝9，所以 a－3＝6，即 6 号出发；②设这七天的日期和是 63 的 2 倍，即 126，则 7a＝126，a＝18，所以 a－3＝15，即 15 号出发；③设这七天的日期和是 63 的 3 倍，即 189，则 7a＝189，a＝27，所以 a－3＝24，即 24 号出发，所以他们可能于五月 6 号或 15 号或 24 号出发