【数学】陕西省延安市吴起高级中学2019-2020学年高一下学期第四次质量检测（期末）试题

【数学】陕西省延安市吴起高级中学2019-2020学年高一下学期第四次质量检测（期末）试题

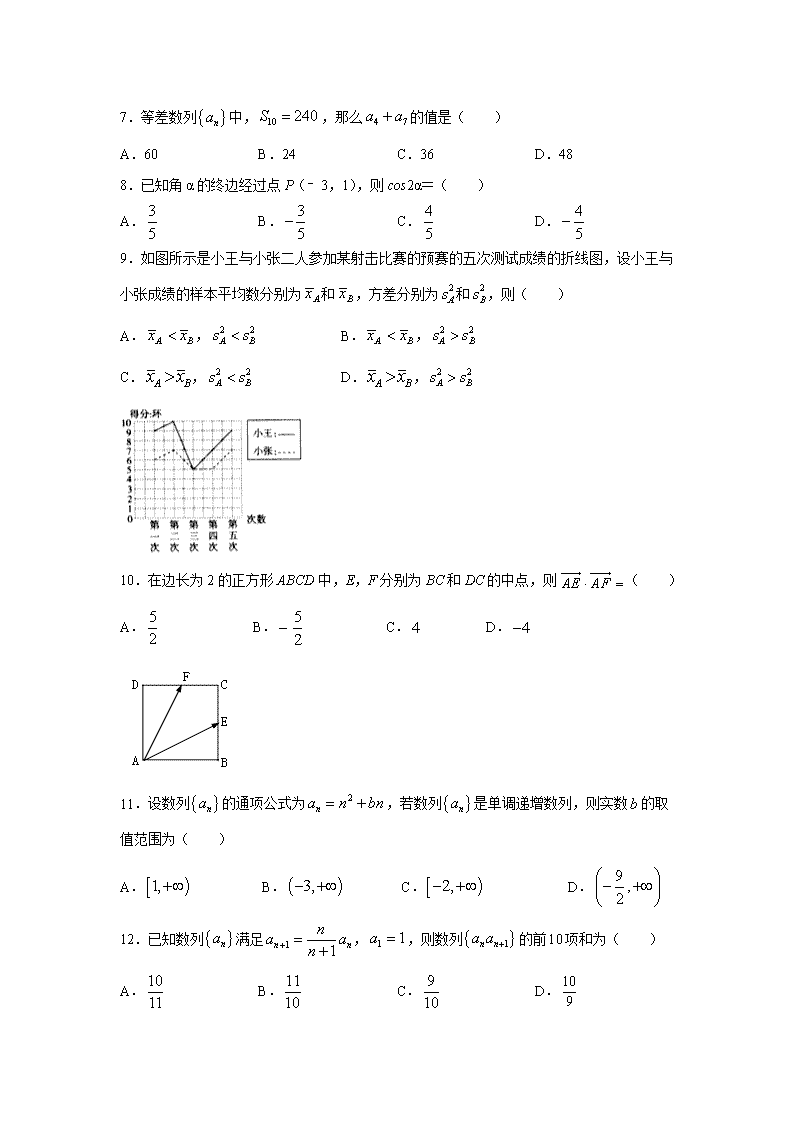
陕西省延安市吴起高级中学2019-2020学年高一下学期第四次质量检测（期末）数学试题 满分150分 答题时间120分钟 一、 选择题（本大题共12小题，每题5分，共计60分．在每小题给出的四个选项中只有一项是符合题目要求的．）‎ ‎1．某企业用自动化流水线生产统一规格的产品，每天上午的四个小时开工期间，每隔分钟抽取一件产品作为样本，则这样的抽样方法是（ ）‎ A．简单随机抽样 B．系统抽样 C．分层抽样 D．以上三种方法都有 ‎2．如图，边长为2的正方形中有一阴影区域，在正方形中随机撒一粒豆子，它落在阴影区域内的概率为，则阴影区域的面积约为（ ）‎ A． B． C． D．无法计算 ‎3．从装有2个红球和2个黑球的口袋内任取两个球，那么互斥而不对立的事件是（ ）‎ A．至少有一个黑球与都是黑球 B．至少有一个黑球与至少有一个红球 C．恰好有一个黑球与恰好有两个黑球 D．至少有一个黑球与都是红球 ‎4．在等比数列中，如果，那么等于（ ）‎ A．2 B． C． D．4‎ ‎5．两个线性相关变量x，y，满足如下关系 x ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ y ‎2.2‎ ‎4.3‎ ‎4.8‎ ‎6.5‎ ‎7.2‎ 则y与x的线性回归直线一定过其样本点的中心，其坐标为（　　）‎ A． B． C． D．‎ ‎6．下列叙述正确的是（ ）‎ A．互斥事件一定不是对立事件，但是对立事件一定是互斥事件 B．若事件发生的概率为，则 C．频率是稳定的，概率是随机的 D．5张奖券中有一张有奖，甲先抽，乙后抽，那么乙比甲抽到有奖奖券的可能性小 ‎7．等差数列中，，那么的值是（ ）‎ A．60 B．24 C．36 D．48‎ ‎8．已知角α的终边经过点P（﹣3，1），则cos2α＝（ ）‎ A． B． C． D．‎ ‎9．如图所示是小王与小张二人参加某射击比赛的预赛的五次测试成绩的折线图，设小王与小张成绩的样本平均数分别为和，方差分别为和，则（ ）‎ A．， B．， ‎ C．， D．，‎ ‎10．在边长为2的正方形ABCD中，E，F分别为BC和DC的中点，则（ ）‎ A． B． C． D．‎ ‎11．设数列的通项公式为，若数列是单调递增数列，则实数的取值范围为（ ）‎ A． B． C． D．‎ ‎12．已知数列满足，，则数列的前项和为（ ）‎ A． B． C． D．‎ 二、填空题（本大题共4小题，每题5分，共计20分．请将正确答案直接填在答题卡的相应位置.）‎ ‎13．抛掷一枚质地均匀的骰子（六个面上的点数分别为1，2，3，4，5，6），事件A为“正面朝上的点数为3”，事件B为“正面朝上的点数为偶数”，则________.‎ ‎14．已知向量，，则________‎ ‎15．数列中为的前n项和，若，则 .‎ ‎16．若将函数的图像向右平移个单位，所得图像关于轴对称，则的最小正值是________.‎ 三、解答题（本大题共6小题，共计70分．解答时应写出必要的文字说明、证明过程或演算步骤.）‎ ‎17．（10分）为了选拔参加自行车比赛的选手，对自行车运动员甲、乙两人在相同条件下进行了6次测试，测得他们的最大速度（单位：m/s）的数据如下：‎ 甲 ‎27‎ ‎38‎ ‎30‎ ‎37‎ ‎35‎ ‎31‎ 乙 ‎33‎ ‎29‎ ‎38‎ ‎34‎ ‎28‎ ‎36‎ ‎（1）画出甲、乙两人6次测试的最大速度的茎叶图；‎ ‎（2）估计甲、乙两运动员的最大速度的平均数和方差，并判断谁参加比赛更合适．‎ ‎18．（12分）记为等差数列的前项和，已知．‎ ‎（1）求的通项公式；‎ ‎（2）若，求．‎ ‎19．（12分）已知（为常数）.‎ ‎（1）求的单调递增区间；‎ ‎（2）若当时，的最大值为4，求的值.‎ ‎20．（12分）已知在等比数列中，，且是和的等差中项.‎ ‎（1）求数列的通项公式；‎ ‎（2）若数列满足，求的前项和.‎ ‎21．（12分）已知数列的前n项和为，且．‎ ‎（1）求数列的通项公式；‎ ‎（2）若，设数列的前n项和为，证明．‎ ‎22.（12分）自由购是一种通过自助结算购物的形式．某大型超市为调查顾客自由购的使用情况，随机抽取了100人，调查结果整理如下：‎ ‎20以下 ‎[20，30）‎ ‎[30，40）‎ ‎[40，50）‎ ‎[50，60）‎ ‎[60，70]‎ ‎70以上 使用人数 ‎3‎ ‎12‎ ‎17‎ ‎6‎ ‎4‎ ‎2‎ ‎0‎ 未使用人数 ‎0‎ ‎0‎ ‎3‎ ‎14‎ ‎36‎ ‎3‎ ‎0‎ ‎（1）现随机抽取1名顾客，试估计该顾客年龄在[30，50）且未使用自由购的概率；‎ ‎（2）从被抽取的年龄在[50，70]使用的自由购顾客中，随机抽取2人进一步了解情况，求这2人年龄都在[50，60）的概率；‎ ‎（3）为鼓励顾客使用自由购，该超市拟对使用自由购顾客赠送1个环保购物袋．若某日该超市预计有5000人购物，试估计该超市当天至少应准备多少个环保购物袋？‎ ‎【参考答案】‎ 一、选择题 ‎1.B 2.C 3.C 4.D 5.A 6.B 7.D 8.C 9.D 10.C 11.B 12.A 二、填空题 ‎13. 14.2 15.6 16.‎ 三、解答题 ‎17.解：（1）茎叶图如下：‎ ‎（2）甲的平均数为：=33，‎ 乙的平均数为：（28+29+33+34+36+38）=33，‎ 甲的方差为：，‎ 乙的方差为：，‎ 甲、乙的平均数相等，乙的方差更小，则乙的发挥更稳定，故乙参加比赛更合适．‎ ‎18.解：（1）设等差数列{an}的公差为d，则，解得a1=1，d=，‎ ‎∴数列的通项公式为=（n+1）．‎ ‎（2）由（1），根据等差数列的求和公式，得，‎ 整理，得m2+3m-108=0，由m∈N*，解得m=9．‎ ‎19.解：（1）由得，‎ 所以，递增区间为；‎ ‎（2），，‎ ‎，‎ 的最大值为2，‎ 在，的最大值为4，‎ ‎，‎ ‎．‎ ‎20.解：（1）设等比数列的公比为，则，则，，‎ 由于是和的等差中项，即，即，解得.‎ 因此，数列的通项公式为；‎ ‎（2），‎ ‎.‎ ‎21.解：（1）当时，得，‎ 当时，得 ，所以.‎ ‎（2）由（1）得： ，‎ 又 ①‎ 得 ②‎ 两式相减得： ，‎ 故 ，‎ 所以 .‎ ‎22．解：（1）随机抽取的100名顾客中，年龄在[30，50）且未使用自由购的有3+14＝17人，‎ 所以随机抽取一名顾客，该顾客年龄在[30，50）且未参加自由购的概率估计为．‎ ‎（2）设事件A为“这2人年龄都在[50，60）”.‎ 被抽取的年龄在[50，60）的4人分别记为a1，a2，a3，a4，‎ 被抽取的年龄在[60，70]的2人分别记为b1，b2，‎ 从被抽取的年龄在[50，70]的自由购顾客中随机抽取2人 共包含15个基本事件，‎ 分别为a1a2，a1a3，a1a4，a1b1，a1b2，a2a3，a2a4，a2b1，a2b2，a3a4，‎ a3b1，a3b2，a4b1，a4b2，b1b2，‎ 事件A包含6个基本事件，‎ 分别为a1a2，a1a3，a1a4，a2a3，a2a4，a3a4，‎ 则；‎ ‎（3）随机抽取的100名顾客中，使用自由购的有3+12+17+6+4+2＝44人，‎ 所以该超市当天至少应准备环保购物袋的个数估计为．‎