2019年高三11月摸底考试数学（文、理科）试题

2019年高三11月摸底考试数学（文、理科）试题

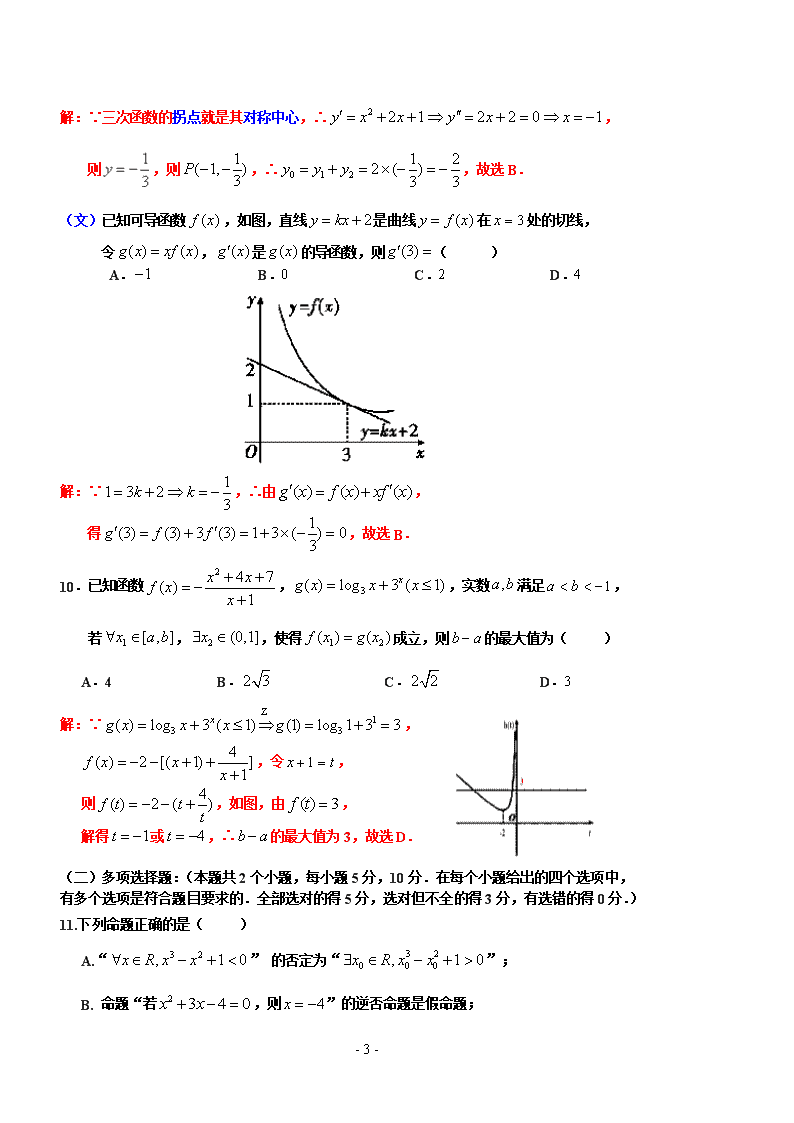
‎2019年高三11月摸底考试数学（文、理科）试题 一、选择题：‎ ‎（一）单项选择题：（本题共10个小题，每小题5分，共50分．在每个小题给出的四个选项中，‎ 只有一项是符合题目要求的）‎ ‎1．已知集合，，若，则（ ）‎ A．2 B．‎3 C．2或3 D．2或4‎ 解：∵，又，‎ ‎∴，由，得2或3，故选C．‎ ‎2．已知 ，其中是实数，是虚数单位，则（ ）‎ A．3 B．‎2 C．5 D．‎ 通解：∵，∴，则，故选D．‎ 另解：∵，‎ ‎∴，，则，故选D．‎ ‎3．已知函数，若，则实数的值为（ ）‎ A． B． C．4 D．‎ 解：∵，∴，由，得(舍正)，故选B．‎ ‎4．若偶函数在上是增函数，且，则不等式的解集为（ ）‎ A． B． C． D．‎ 解：当时，需；当时，需，画图，知解集是，故选A．‎ ‎5．函数的图象大致是（ ）‎ A． B．‎ ‎- 9 -‎ C． D．‎ 解：函数为偶函数，则图像关于轴对称，排除B；‎ 当时，，求导得，由，‎ ‎，则在上单调递减，在上单调递增，故选D．‎ ‎6．已知向量，向量，且，则的值是（ ）‎ A． B． C． D．‎ 解：∵，∴，则，故选D．‎ ‎7．将函数图象向左平移个单位，所得函数图象的一条对称轴方程是（ ）‎ A． B． C． D．‎ 解：∵，‎ ‎∴将代入可得最大值，故选C．‎ ‎8．中国古代数学名著《算法统宗》，由明代数学家程大位编著，它对我国民间普及珠算和数学知识 起到了重大意义，是东方古代数学名著．在这部著作中，许多问题都是以歌诀形式呈现，“九儿 问甲歌” 就是其中一首：一个公公九个儿，若问生年总不知，自长排来差三岁，共年二百又零七，借问长儿多少岁，各儿岁数要详推．请问长儿多少岁？（ ）‎ A．11 B． C． D．‎ 解：∵构成一个等差数列：，，求，‎ ‎∴，解得，故选C．‎ ‎9．（理）已知函数的图象上存在一点满足：若过点的直线与曲线交 于不同于的两点，，且恒有为定值，则的值为（ ）‎ A． B． C． D．‎ ‎- 9 -‎ 解：∵三次函数的拐点就是其对称中心，∴，‎ 则，则，∴，故选B．‎ ‎（文）已知可导函数，如图，直线是曲线在处的切线，‎ 令，是的导函数，则（ ）‎ A． B．‎0 C．2 D．4‎ 解：∵，∴由，‎ 得，故选B．‎ ‎10．已知函数，，实数满足，‎ ‎ 若，，使得成立，则的最大值为（ ）‎ A．4 B． C． D．3‎ 解：∵，‎ ‎，令，‎ 则，如图，由，‎ 解得或，∴的最大值为3，故选D．‎ ‎（二）多项选择题：（本题共2个小题，每小题5分，10分．在每个小题给出的四个选项中，‎ 有多个选项是符合题目要求的．全部选对的得5分，选对但不全的得3分，有选错的得0分．）‎ ‎11.下列命题正确的是（ ）‎ A.“” 的否定为“”；‎ B. 命题“若，则”的逆否命题是假命题；‎ ‎- 9 -‎ C. 在△ABC中，“”是“”的充要条件；‎ D. 函数的对称中心是．‎ 解：A错：应改为；B、C显然对；‎ ‎ D错：应改为，故选B、C．‎ ‎12．定义在上函数对任意两个不相等的实数都有 ‎，则称函数为“函数”，‎ 以下函数中“函数”的是（ ）‎ A． B．‎ C． D．‎ 解：∵，‎ 即，故函数单调递增，画图，可知A、C不符合，‎ ‎∴由多选特征知B、D正确(注：B可用求导来验证)，故选B、D．‎ 二、填空题：（本题共4小题，每小题5分，共20分．‎ ‎13．函数的定义域为 ．‎ 解：∵，∴，故其定义域为．‎ 注：许多学生误理解为．‎ ‎14．记，当时，观察下列等式：‎ ‎，，，‎ ‎，…，由此可以推测 ．‎ ‎（文）‎ 解：可归纳出各项系数和为1，则，解得．（文）．‎ ‎- 9 -‎ ‎15．设，且，则的最小值为 ．‎ 通解：∵，∴‎ ‎，‎ 当且仅当时取等号，故的最小值为．‎ 妙解：由权方和不等式可得：．‎ ‎16．已知等差数列满足：当时，，‎ 是数列的前项和，则 ， ．‎ ‎（文） ．‎ 解：当时，，则，有；‎ 当时，，则，有；‎ 当时，，则，有；‎ 当时，，则，有；‎ 当时，，则，有，‎ 则（理），．（文），．‎ 三、解答题：（本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）‎ ‎17. （本小题共10分）‎ 已知函数与的定义域是，是偶函数, 是奇函数，且．‎ ‎（1）求函数；‎ ‎（2）若关于的不等式在上恒成立，求实数的取值范围．‎ 解：(1) ∵，①　　∴，……2分 又∵是偶函数, 是奇函数，∴，②……4分 由①②得：；……5分 ‎- 9 -‎ ‎(2) ∵，∴，‎ ‎∴，……7分 由已知得：，故，……9分 则实数的取值范围是．……10分 ‎18. （本小题共12分）‎ 已知函数．‎ ‎（1）求函数的最小值和最小正周期；‎ ‎（2）求函数的单调递增区间．‎ 解：(1) ∵，……4分 ‎∴的最小值是，最小正周期是；……6分 ‎(2) 由，，……8分 得，……10分 故函数的单调递增区间为，．……12分 ‎19. （本小题共12分）‎ 已知是等差数列，各项均为正数的等比数列的公比为，‎ 且满足， ，．‎ ‎（1）求数列，的通项公式；‎ ‎（2）设数列的前项和为，求满足的最小正整数．‎ 解：(1)设的公差为，的公比为，则 ‎，……2分 解得，……4分 ‎- 9 -‎ 故，；……6分 ‎(2) ∵，……8分 ‎∴，……10分 即，，故最小正整数是7．……12分 ‎20. （本小题共12分）‎ 在中，若．‎ ‎（1）求角的大小；‎ ‎（2）若，的面积为，试判断的形状，并说明理由．‎ 解：(1) ∵，……2分 ‎∴，‎ 又∵，∴，……4分 ‎∵，∴；……6分 ‎(2) ∵，∴，……8分 又∵，∴，……10分 由韦达定理解得，而，故是等边三角形．……12分 ‎21. （本小题共12分）‎ 某快递公司在某市的货物转运中心，拟引进智能机器人分拣系统，以提高分拣效率 和降低物流成本，已知购买x台机器人的总成本万元．‎ ‎(1)若使每台机器人的平均成本最低，问应买多少台？‎ ‎(2)现按(1)中的数量购买机器人，需要安排m人将邮件放在机器人上，机器人 将邮件送达指定落袋口完成分拣．经实验知，每台机器人的日平均分拣量 ‎ (单位：件)，已知传统人工分拣每人每 ‎- 9 -‎ 日的平均分拣量为1 200件，问引进机器人后，日平均分拣量达最大值时，‎ 用人数量比引进机器人前的用人数量最多可减少百分之几？‎ 解：(1)由总成本万元，可得每台机器人的平均成本 ‎＝＝x＋＋1≥2＋1＝2. ……4分 当且仅当x＝，即x＝300时，上式等号成立．‎ ‎∴若使每台机器人的平均成本最低，应买300台．……6分 ‎(2)引进300台机器人后，‎ ‎①当1≤m≤30时，300台机器人的日平均分拣量为‎160m(60－m)＝－‎160m2‎＋9 ‎600m，‎ ‎∴当m＝30时，日平均分拣量有最大值144 000件．……8分 ‎②当m＞30时，日平均分拣量为470×300＝141 000(件)．‎ ‎∴300台机器人的日平均分拣量的最大值为144 000件．……10分 若传统人工分拣144 000件，则需要人数为＝120(人)．‎ ‎∴日平均分拣量达最大值时，用人数量比引进机器人前 的用人数量最多可减少×100%＝75%.……12分 ‎22. （本小题共12分）‎ 设函数．‎ ‎（1）（理）设，试讨论的单调性；‎ ‎（文）求函数的最小值；‎ ‎ (2) 斜率为直线与曲线交于两点，‎ ‎ 求证：． ‎ 解：(1) （文） ∵，令，得．……2分 当时，；当时，，‎ ‎∴当时，；……4分 ‎- 9 -‎ ‎（理），则，……2分 ‎①当时，恒有，在上是增函数；……3分 ‎②当时，令，得，解得；‎ 令，得，解得．‎ 综上，当时，在上是增函数；当时，‎ 在单调递增，在单调递减；……5分 ‎ (2) ∵，‎ 要证明，只需证明．……6分 法一：只要证，令，只要证，由知，‎ 只要证．（*）……8分 ‎①设，则，故在是增函数，‎ ‎∴当时，，即；……10分 ‎②设，则，故在是增函数，‎ ‎∴当时，，即．‎ ‎　　　由①②知（*）式成立，故得证．……12分 法二：由对数平均值不等式：，‎ 得，且，故原式得证．‎ ‎- 9 -‎