圆锥曲线常用的二级结论

圆锥曲线常用的二级结论

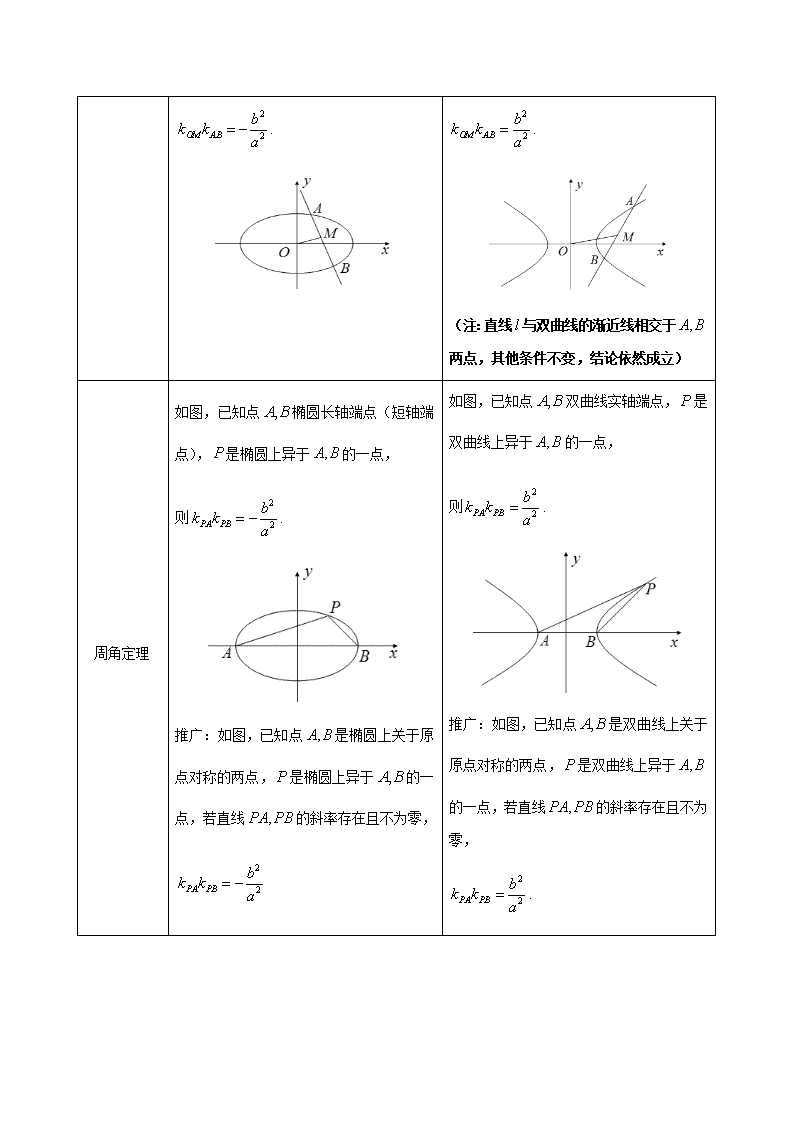
圆锥曲线常用的二级结论 椭圆与双曲线对偶结论 椭圆 双曲线 标准方程 焦点 焦点 焦半径 为离心率，为点的横坐标.‎ 为离心率，为点的横坐标.‎ 焦半径范围 为椭圆上一点，为焦点.‎ 为双曲线上一点，为焦点.‎ 通径 过焦点与长轴垂直的弦称为通径.‎ 通径长为 过焦点与实轴垂直的弦称为通径.‎ 通径长为 如图，直线过焦点与椭圆相交于两点.则的周长为.‎ ‎（即）‎ 如图，直线过焦点与双曲线相交于两点.则.‎ 焦点弦 倾斜角为的直线过焦点与椭圆相交于两点.‎ 焦点弦长.‎ 最长焦点弦为长轴，最短焦点弦为通径.‎ 倾斜角为的直线过焦点与双曲线相交于两点.‎ 焦点弦长.‎ 与数量关系 直线过焦点与椭圆相交于两点，则.‎ 直线过焦点与双曲线相交于两点，则.‎ 已知点是椭圆上一点，坐标原点，‎ 则.‎ 已知点是双曲线上一点，坐标原点，‎ 则.‎ 焦三角形 如图，是椭圆上异于长轴端点的一点，已知，，‎ ‎，则 ‎（1）；‎ ‎（2）离心率.‎ 如图，是双曲线上异于实轴端点的一点，已知，，‎ ‎，则 ‎（1）；‎ ‎（2）离心率.‎ 垂径定理 如图，已知直线与椭圆相交于两点，点为的中点，为原点，则 如图，已知直线与双曲线相交于两点，点为的中点，为原点，则 ‎.‎ ‎.‎ ‎（注：直线与双曲线的渐近线相交于两点，其他条件不变，结论依然成立）‎ 周角定理 如图，已知点椭圆长轴端点（短轴端点），是椭圆上异于的一点，‎ 则.‎ 推广：如图，已知点是椭圆上关于原点对称的两点，是椭圆上异于的一点，若直线的斜率存在且不为零，‎ 如图，已知点双曲线实轴端点，是双曲线上异于的一点，‎ 则.‎ 推广：如图，已知点是双曲线上关于原点对称的两点，是双曲线上异于的一点，若直线的斜率存在且不为零，‎ ‎.‎ 直线过焦点与椭圆相交于两点，点，‎ 则（即）.‎ 直线过焦点与双曲线相交于两点，点，‎ 则（即）.‎ 切线方程 已知点是椭圆上一点，则椭圆在点处的切线方程为.‎ 已知点是双曲线上一点，则双曲线在点处的切线方程为.‎ 双曲线的结论 ‎1．过定点（定点在双曲线外且不在渐近线上）的直线与双曲线交点个数问题：‎ 设斜率为的直线过定点，双曲线方程为，过点与双曲线相切时的斜率为.‎ ‎（1）当时，直线与双曲线有两个交点，且这两交点在双曲线的两支上；‎ ‎（2）当时，直线与双曲线只有一个交点；‎ ‎（3）当时，直线与双曲线有两个交点，且这两交点在双曲线的同一支上；‎ ‎（4）当时，直线与双曲线只有一个交点；‎ ‎（5）当时，直线与双曲线没有交点.‎ ‎2．如图，是双曲线的焦点，过点作垂直双曲线的其中一条渐近线，垂足为，为原点，则.‎ ‎3．点是双曲线上任意一点，则点到双曲线的渐近线的距离之积为定值.‎ ‎4．点是双曲线上任意一点，过点作双曲线的渐近线的平行线分别与渐近线相交于两点，为原点，则平行四边形的面积为定值.‎ 抛物线的结论 如图，抛物线方程为，准线与轴相交于点，过焦点的直线与抛物线相交于，两点，为原点，直线的倾斜角为.‎ ‎1．‎ ‎2．焦半径：，，.‎ ‎3．焦点弦：.‎ ‎4．的数量关系：，.‎ ‎5．三角形的面积.‎ ‎6．以焦点弦为直径的圆与准线相切；以焦半径为直径的圆与轴相切.‎ ‎7．直线的斜率之和为零（），即.‎ ‎8．点三点共线；点三点共线.‎ ‎9．如图，点是抛物线，为原点，若，则直线过定点.‎