- 2021-06-30 发布 |
- 37.5 KB |
- 5页
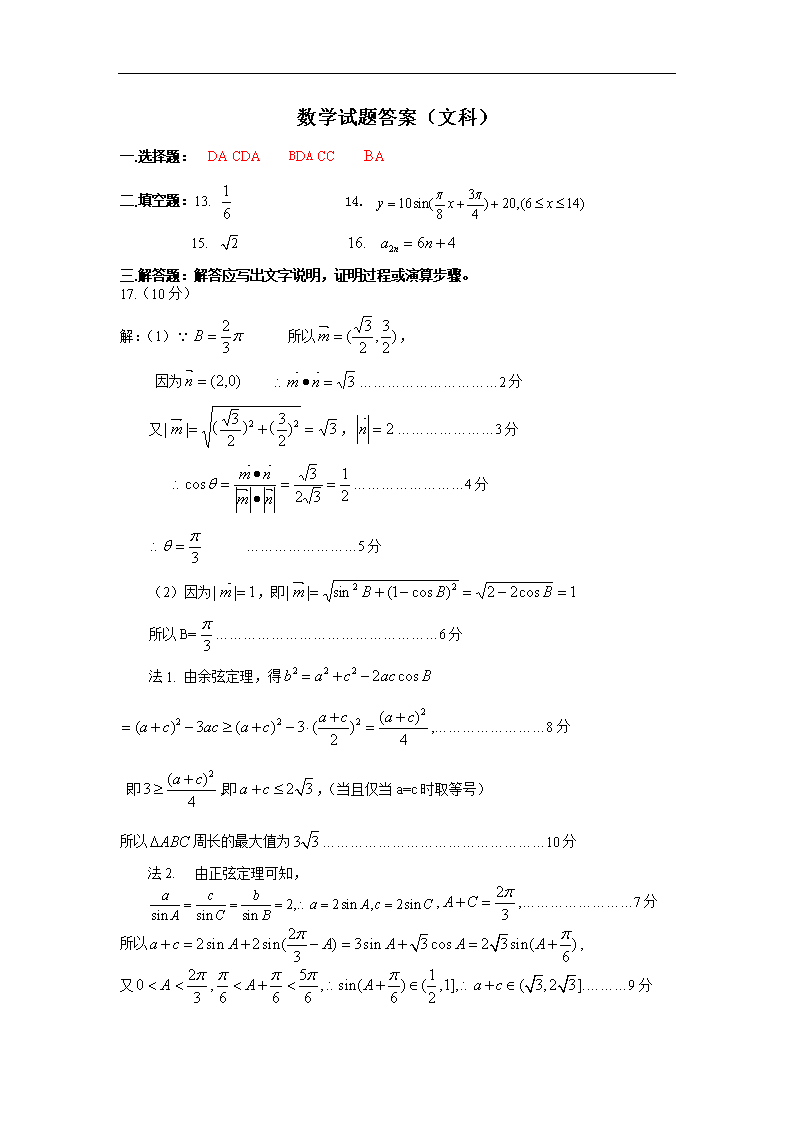


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
河北省保定市唐县第一中学2020届高三1月寒假调研考试数学(文)答案
数学试题答案(文科) 一.选择题: DA CDA BDA CC BA 二.填空题:13. 14. 三.解答题:解答应写出文字说明,证明过程或演算步骤。 17.(10分) 解:(1) 所以, 因为 …………………………2分 又,…………………3分 ……………………4分 ……………………5分 (2)因为,即 所以B=…………………………………………6分 法1. 由余弦定理,得 ,……………………8分 即,即,(当且仅当a=c时取等号) 所以周长的最大值为…………………………………………10分 法2. 由正弦定理可知, ,,……………………7分 所以, 又,………9分 所以当时, 所以周长的最大值为………………………………………10分 18. 解:(1)由且得: 所以 又因为数列为等比数列,所以可知其首项为4,公比为2. ……………3分 故 所以……………………5分 (2)由 ……………………6分 令 累加得, ……………………10分 又满足上式 ……………………12分 19.( 12分) (1)解:取的中点,的中点,连接.因为,且平面平面, 所以平面,同理平面,……………………3分 又因为, 所以.……………………6分 C D F E O G A B (2)证明:设平面AGF∩平面ABC=AP,AP∩BC=P 因为平面ABC∥平面DFE,所以AP∥FG…………………8分 因为ED,ED∥BC, 所以AP⊥BC, 即P与O重合, 所以FG=AO……………………10分 所以四边形为平行四边形,所以, 又,所以平面平面……………………12分 20.(12分) 解(1)依题意得,解得…………3分 椭圆的方程为.………………4分 (2)易知直线的斜率存在,并设直线方程为,将其代入, 化简得,……………………6分 设、 , 且……………………8分 依题意可知, 即, .……………………10分 将代入上式得 化简得,所以 故所求的直线方程为……………………………………12分 21.(12分) 解:(1)众数为157,共出现3次. ……………………2分 前五天污染指数平均值为………………4分 (2)①在2月1日——12日这12天中,只有在1日、11日、12日3天时,其接下来的两天才会遭遇重度及以上污染天气,故 所求的概率为……………………8分 ②法1:由①知,“此人外出期间其接下来的两天期间都避不开重度及以上污染”对应的到达日期为:1日、11日、12日. 所以所求的概率为……………………12分 法2:根据题意,事件“此人接下来的两天至少有1天能避开空气重度及以上污染”,包括两种情况: (i)连续两天都避开重度及以上污染; 由折线图易知,在3日、4日、7日、8日、9日时,其接下来的两天都能避开重度及以上污染天气 此时,所求的概率为……………………10分 (ii)恰有一天有重度及以上污染 由折线图易知,在2日、5日、6日、10日时,其接下来的两天恰有一天能避开重度及以上污染天气 此时,所求的概率为 故所求的概率为P=.------------------12分 22.(12分) 解: (1) ,…………① 所以即…… ② 由①②联立解得: . ……………………………………………3分 (2)设, , 依题意知:当时, ……………………4分 又在(-1,1)上恒成立 所以在[-1,1]上单调递减 ……………………………………6分 在上单调递增, 解得: 实数的取值范围为.…………………8分 (3) 的图象如图所示: 令,则 ……………………9分 当时有1个解-3, ……………………10分 当时有2个解:、ln3, ……………………11分 当时有个解: ln(3+ln4)、. 故方程的解分别为: -3, 、ln3, ln(3+ln4)、…………………………12分查看更多