2017年北京市海淀区高考数学一模试卷(文科)
2017年北京市海淀区高考数学一模试卷(文科)
一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合A={x|1
4},则集合A∩B等于( )
A.{x|x>1} B.{x|22}
2. 圆心为(0, 1)且与直线y=2相切的圆的方程为( )
A.(x+1)2+y2=1 B.(x−1)2+y2=1 C.x2+(y−1)2=1 D.x2+(y+1)2=1
3. 执行如图所示的程序框图,输出的x的值为( )
A.3 B.4 C.2 D.1
4. 若实数a,b满足a>0,b>0,则“a>b”是“a+lna>b+lnb”的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
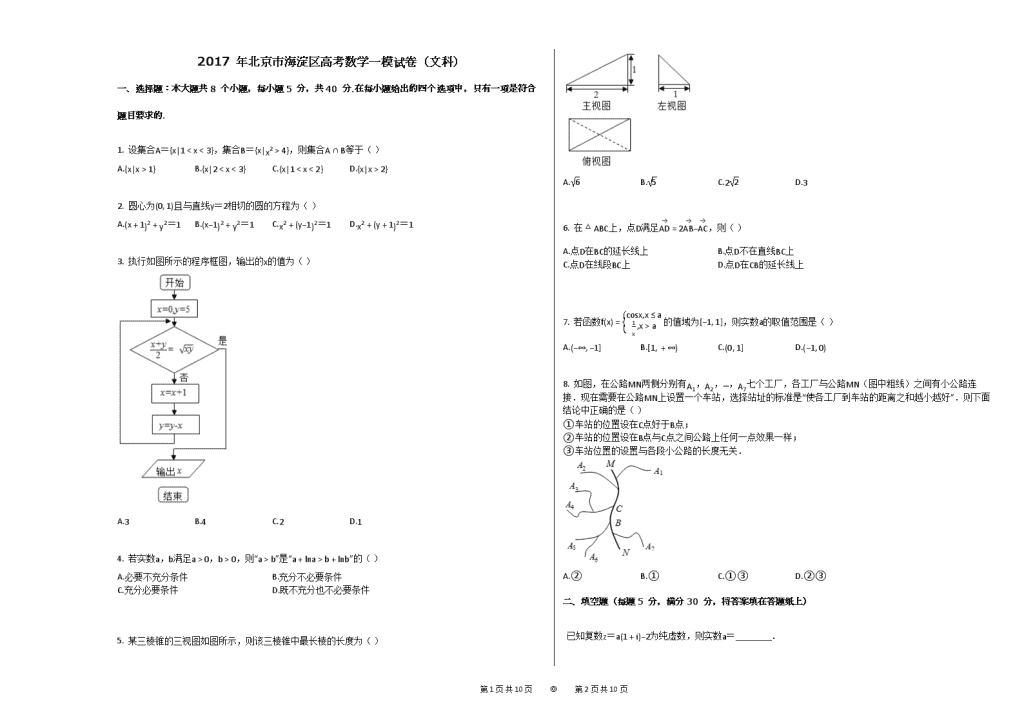
5. 某三棱锥的三视图如图所示,则该三棱锥中最长棱的长度为( )
A.6 B.5 C.22 D.3
6. 在△ABC上,点D满足AD→=2AB→−AC→,则( )
A.点D在BC的延长线上 B.点D不在直线BC上
C.点D在线段BC上 D.点D在CB的延长线上
7. 若函数f(x)=cosx,x≤a1x,x>a 的值域为[−1, 1],则实数a的取值范围是( )
A.(−∞, −1] B.[1, +∞) C.(0, 1] D.(−1, 0)
8. 如图,在公路MN两侧分别有A1,A2,…,A7七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
①车站的位置设在C点好于B点;
②车站的位置设在B点与C点之间公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关.
A.② B.① C.①③ D.②③
二、填空题(每题5分,满分30分,将答案填在答题纸上)
已知复数z=a(1+i)−2为纯虚数,则实数a=________.
第9页 共10页 ◎ 第10页 共10页
已知等比数列{an}中,a2a4=a5,a4=8,则公比q=________,其前4项和S4=________.
若抛物线y2=2px的准线经过双曲线x2−y23=1的左焦点,则实数p=________.
若x,y满足x+2y−4=0x−2y≤0x≥1 则yx的最大值是________.
已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=________,a的最小值是________.
阅读下列材料,回答后面问题:
在2014年12月30日CCTV13播出的“新闻直播间”节目中,主持人说:“…加入此次亚航失联航班QZ8501被证实失事的话,2014年航空事故死亡人数将达到1320人.尽管如此,航空安全专家还是提醒:飞机仍是相对安全的交通工具.①________;②________.”
对上述航空专家给出的①、②两段表述(划线部分),你认为不能够支持“飞机仍是相对安全的交通工具”的所有表述序号为________,你的理由是________
________.
三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)
已知等差数列{an}满足a1+a2=6,a2+a3=10.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an+an+1}的前n项和.
某地区以“绿色出行”为宗旨开展“共享单车”业务.该地有a,b两种“共享单车”(以下简称a型车,b型车).某学习小组7名同学调查了该地区共享单车的使用情况.
(Ⅰ)某日该学习小组进行一次市场体验,其中4人租到a型车,3人租到b型车.如果从组内随机抽取2人,求抽取的2人中至少有一人在市场体验过程中租到a型车的概率;
(Ⅱ)根据已公布的2016年该地区全年市场调查报告,小组同学发现3月,4月的用户租车情况城现如表使用规律.例如,第3个月租a型车的用户中,在第4个月有60%的用户仍租a型车.
第3个月
第4个月
租用a型车
租用b型车
租用a型车
60%
50%
租用b型车
40%
50%
若认为2017年该地区租用单车情况与2016年大致相同.已知2017年3月该地区租用a,b两种车型的用户比例为1:1,根据表格提供的信息,估计2017年4月该地区租用两种车型的用户比例.
在△ABC中,A=2B.
(Ⅰ)求证:a=2bcosB;
(Ⅱ)若b=2,c=4,求B的值.
在四棱锥P−ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.
(Ⅰ)求证:PB // 平面FAC;
(Ⅱ)求三棱锥P−EAD的体积;
(Ⅲ)求证:平面EAD⊥平面FAC.
已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右顶点分别为A,B,且|AB|=4,离心率为12.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点Q(4, 0),若点P在直线x=4上,直线BP与椭圆交于另一点M.判断是否存在点P,使得四边形APQM为梯形?若存在,求出点P的坐标;若不存在,说明理由.
已知函数f(x)=ex−x2+ax,曲线y=f(x)在点(0, f(0))处的切线与x轴平行.
(Ⅰ)求a的值;
(Ⅱ)若g(x)=ex−2x−1,求函数g(x)的最小值;
(Ⅲ)求证:存在c<0,当x>c时,f(x)>0.
第9页 共10页 ◎ 第10页 共10页
参考答案与试题解析
2017年北京市海淀区高考数学一模试卷(文科)
一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
【答案】
此题暂无答案
【考点】
交集根助运算
【解析】
此题暂无解析
【解答】
此题暂无解答
2.
【答案】
此题暂无答案
【考点】
直线与都连位置关系
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
此题暂无答案
【考点】
程正然图
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
此题暂无答案
【考点】
充分常件、头花条件滤充要条件
【解析】
此题暂无解析
【解答】
此题暂无解答
5.
【答案】
此题暂无答案
【考点】
由三都问求体积
【解析】
此题暂无解析
【解答】
此题暂无解答
6.
【答案】
此题暂无答案
【考点】
向量的明角轮法则
【解析】
此题暂无解析
【解答】
此题暂无解答
7.
【答案】
此题暂无答案
【考点】
分段水正的应用
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
此题暂无答案
【考点】
进行简根的合情亮理
【解析】
此题暂无解析
【解答】
此题暂无解答
二、填空题(每题5分,满分30分,将答案填在答题纸上)
【答案】
此题暂无答案
【考点】
复三的刺算
【解析】
此题暂无解析
【解答】
此题暂无解答
第9页 共10页 ◎ 第10页 共10页
【答案】
此题暂无答案
【考点】
等比数表的弹项公式
等比数使的前n种和
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
抛物使之性质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
简单因性规斯
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
由y=于si械(ωx+美)的部分角象六定其解断式
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
收集于据的叫法
【解析】
此题暂无解析
【解答】
此题暂无解答
三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.)
【答案】
此题暂无答案
【考点】
数于术推式
数使的种和
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
列举法体算土本母件数及骨件发生的概率
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
余于视理
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
柱体三锥州、台到的体建计算
平面因平面京直
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
直线与椭常画位置关系
椭明的钾用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
利验热数技究女数的最值
利用三数定究曲纵上迹点切线方程
第9页 共10页 ◎ 第10页 共10页
【解析】
此题暂无解析
【解答】
此题暂无解答
第9页 共10页 ◎ 第10页 共10页