【数学】2018届一轮复习苏教版第69课时立体几何综合学案

【数学】2018届一轮复习苏教版第69课时立体几何综合学案

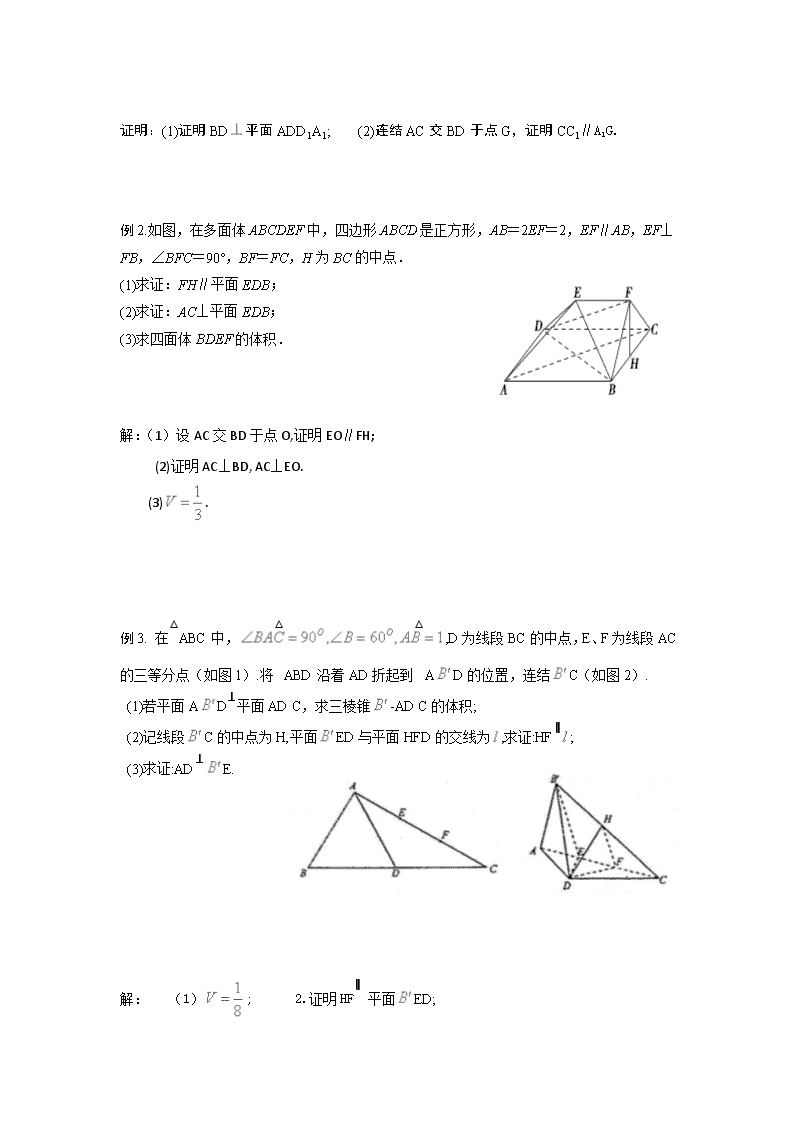
第69课时 立体几何综合 ‎【学习目标】‎ ‎1.熟练运用线线、线面、面面位置关系的性质和判定，提高逻辑推理能力；‎ ‎2.能解决空间几何体的侧面积、表面积和体积的简单计算；‎ ‎3.体会空间问题平面化的降维思想，培养空间想象能力.‎ ‎【自主练习 】‎ ‎1. 棱长为a正四面体的相邻两个侧面所成角的余弦值是 ，侧棱与底面所成角的正弦值是 .‎ ‎2. 设三棱锥S-ABC的三条侧棱两两垂直，且长分别为‎2a、a、a，其外接球的表面积为 .‎ P A B C ‎3. 正三棱锥中，， ，分别是棱上的点，为边的中点，，则三角形的面积为____.‎ ‎4. 一个圆柱的轴截面是正方形，其侧面积与一个球的表面积相等，那么这个圆柱的体积与这个球的体积之比为 .‎ ‎5. 正三棱柱的侧面展开图是边长分别为2和4的矩形，则它的体积为 ． ]‎ ‎6. 将一个半径为‎5cm的水晶球放在如图所示的工艺架上，支架是由三根金属杆PA、PB、PC组成，它们两两成600角.则水晶球的球心到支架P的距离是 cm.‎ 答案：‎ ‎1.； 2. ； 3.； 4.； 5.； 6.10.‎ ‎3‎ ‎【典型例题】‎ 例1.如图，在四棱台ABCD-A1B‎1C1D1中，D1D⊥平面ABCD，底面ABCD是平行四边形，AB＝2AD，AD＝A1B1，∠BAD＝60°.‎ ‎(1)证明：AA1⊥BD；‎ ‎(2)证明：CC1∥平面A1BD.‎ 证明：(1)证明BD平面ADD‎1A1; (2)连结AC交BD于点G，证明CC1∥A‎1G.‎ 例2.如图，在多面体ABCDEF中，四边形ABCD是正方形，AB＝2EF＝2，EF∥AB，EF⊥FB，∠BFC＝90°，BF＝FC，H为BC的中点．‎ ‎(1)求证：FH∥平面EDB；‎ ‎(2)求证：AC⊥平面EDB；‎ ‎(3)求四面体BDEF的体积．‎ 解：（1）设AC交BD于点O,证明EO∥FH;‎ ‎ (2)证明AC⊥BD, AC⊥EO.‎ ‎(3).‎ 例3. 在△ABC中，,D为线段BC的中点，E、F为线段AC的三等分点（如图1）.将△ABD沿着AD折起到△AD的位置，连结C（如图2）.‎ ‎(1)若平面AD⊥平面AD C，求三棱锥-AD C的体积;‎ ‎(2)记线段C的中点为H,平面ED与平面HFD的交线为,求证:HF∥;‎ ‎(3)求证:AD⊥E.‎ ‎ ‎ 解： （1）; 2.证明HF∥ 平面ED; ‎ ‎(3)证明：取AD中点M，证明AD⊥ 平面MD.‎ ‎ ‎ 解：(1)证明DE⊥平面ACD; (2);‎ ‎ (3)当取最大值时，此时AD=CE=.‎