2020届甘肃省武威第一中学高三上学期12月月考数学（文）试题（解析版）

2020届甘肃省武威第一中学高三上学期12月月考数学（文）试题（解析版）

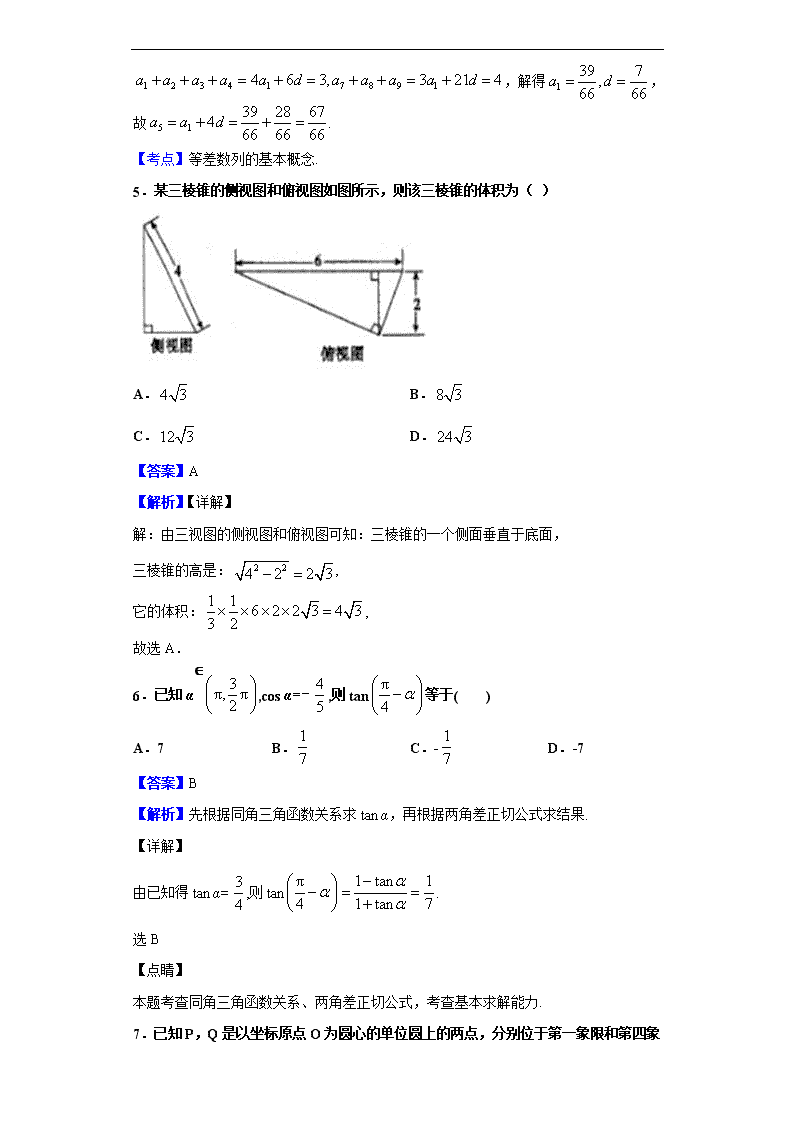
‎2020届甘肃省武威第一中学高三上学期12月月考数学（文）试题 一、单选题 ‎1．设集合,,则下列结论正确的是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】集合,,‎ ‎,所以.‎ 故选C.‎ ‎2．已知复数满足，则（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】试题分析：∴，∴z=，故选C.‎ ‎【考点】复数运算 ‎3．设，则是的( )‎ A．充要条件 B．充分不必要条件 C．必要不充分条件 D．既不充分也不必要条件 ‎【答案】B ‎【解析】试题分析：，，故是的充分不必要条件.‎ ‎【考点】对数不等式；指数不等式；充要条件.‎ ‎4．《九章算术》“竹九节”问题：现有一根九节的竹子，自上而下各节的容积成等差数列，上面4‎ 节的容积共3升，下面3节的容积共4升，则第五节的容积为（ ）‎ A．升 B．升 C．升 D．1升 ‎【答案】A ‎【解析】试题分析：依题意 ‎，解得，故.‎ ‎【考点】等差数列的基本概念.‎ ‎5．某三棱锥的侧视图和俯视图如图所示，则该三棱锥的体积为（ ）‎ A． B．‎ C． D．‎ ‎【答案】A ‎【解析】【详解】‎ 解：由三视图的侧视图和俯视图可知：三棱锥的一个侧面垂直于底面，‎ 三棱锥的高是：,‎ 它的体积：,‎ 故选A．‎ ‎6．已知α∈,cos α=,则tan等于(　　)‎ A．7 B． C．- D．-7‎ ‎【答案】B ‎【解析】先根据同角三角函数关系求tan α，再根据两角差正切公式求结果.‎ ‎【详解】‎ 由已知得tan α=,则tan.‎ 选B ‎【点睛】‎ 本题考查同角三角函数关系、两角差正切公式，考查基本求解能力.‎ ‎7．已知P，Q是以坐标原点O为圆心的单位圆上的两点，分别位于第一象限和第四象限，且点P的纵坐标为，点Q的横坐标为，则（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】根据单位圆上点的坐标与三角函数关系，可得，由同角三角函数关系式可得；由题意可得，由同角三角函数关系可得，而，根据余弦的和角公式即可求解。‎ ‎【详解】‎ 由题意可得，‎ ‎∴‎ 再根据，可得，‎ ‎，‎ 故选D.‎ ‎【点睛】‎ 本题考查了同角三角函数关系式的应用，三角函数的定义，余弦和角公式的用法，属于基础题。‎ ‎8．圆关于直线对称，则ab取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】把圆的方程化为标准方程，找出圆心坐标和半径，由已知圆关于直线对称，得到圆心在直线上，故把圆心坐标代入已知直线方程得到与的关系式，由表示出，设，将表示出的代入中，得到关于的二次函数关系式，由二次函数求最大值的方法即可求出的最大值，即为的最大值，即可写出的取值范围．‎ ‎【详解】‎ 解：把圆的方程化为标准方程得：，‎ 圆心坐标为，半径，‎ 根据题意可知：圆心在已知直线上，‎ 把圆心坐标代入直线方程得：，即，‎ 则设，‎ 当时，有最大值，最大值为，即的最大值为，‎ 则的取值范围是．‎ 故选：．‎ ‎【点睛】‎ 本题以直线与圆为载体，考查对称性，考查了直线与圆相交的性质，以及二次函数的性质．根据题意得到圆心在已知直线上是解本题的关键，属于中档题．‎ ‎9．已知数列满足…（），则（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】由题意得……，两式相除得 ，选A.‎ ‎10．若不等式组,表示的平面区域为三角形，且其面积等于，则m的值为（ ）‎ A．-3 B．1 C． D．3‎ ‎【答案】B ‎【解析】如图，‎ ‎，‎ 由于不等式组,表示的平面区域为，且其面积等于，‎ 再注意到直线与直线互相垂直，所以是直角三角形，‎ 易知，,;从而=，‎ 化简得：，解得,或，检验知当时，已知不等式组不能表示一个三角形区域，故舍去，所以;故选B.‎ ‎【考点】线性规划与三角形的面积.‎ ‎11．已知定义域为的偶函数，其导函数为，对任意正实数满足，若，则不等式的解集是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】试题分析：因为定义域为的偶函数，所以，对任意正实数满足，所以，因为，所以，所以函数在上单调递增，所以在上单调递减，由不等式，所以或，解得或，故选C.‎ ‎【考点】函数的奇偶性与单调性的应用；利用导数研究函数的性质.‎ ‎【方法点晴】本题主要考查了利用导数研究函数的单调性、函数的奇偶性与函数的单调性的应用，本题的解答中根据函数的奇偶性和利用导数判定函数的单调性，得出函数在上单调递增，所以在上单调递减，列出不等式组是解答的关键，着重考查了学生的推理与运算能力，属于中档试题.‎ ‎12．已知函数，若，且对任意的恒成立，则的最大值为 A．3 B．4 C．5 D．6‎ ‎【答案】B ‎【解析】由,则=可化简为,构造函数,,令,即在单调递增,设,因为,,所以,且,故在上单调递减, 上单调递增,所以,又,,即k的最小值为4,故选B.‎ 点睛:本题考查函数的恒成立和有解问题,属于较难题目.首先根据自变量x 的范围,分离参数和变量,转化为新函数g(x)的最值,通过构造函数求导判断单调性,可知在上单调递减, 上单调递增,所以,且,,通过对最小值化简得出的范围,进而得出k的范围.‎ 二、填空题 ‎13．已知向量，若，则代数式________.‎ ‎【答案】3‎ ‎【解析】利用向量共线定理可得，解得．再利用弦化切可得代数式即可．‎ ‎【详解】‎ 解：，，‎ ‎，‎ 解得．‎ 代数式．‎ 故答案为：．‎ ‎【点睛】‎ 本题考查了向量共线定理和三角函数的基本关系式，属于基础题．‎ ‎14．已知函数，则满足的a的取值范围是________（用区间的形式表示）.‎ ‎【答案】‎ ‎【解析】分别讨论：当时与当时两种情况，再结合对数函数与指数函数的性质求出的范围即可．‎ ‎【详解】‎ 解：当时，则有，解得：；‎ 当时，则有，解得：，‎ 所以的取值范围是：．‎ 故答案为：．‎ ‎【点睛】‎ 本题主要考查分段函数，以及考查利用对数函数与指数函数的单调性、特殊点解决不等式问题，考查形式计算能力．‎ ‎15．已知为球的半径，垂直于的平面截球面得到圆（为截面与的交点）.若圆的面积为，，则球的表面积为___________.‎ ‎【答案】‎ ‎【解析】试题分析：由已知可得圆的半径为，取圆上一点，则，在中，球半径，所以所求球的表面积为.‎ ‎【考点】球的表面积．‎ ‎【思路点睛】本题主要考查球的表面积，属基础题.本题关键在于获得球体的半径，由截面圆的面积可得截面圆的半径为，结合垂直于截面圆，可得在垂线上，取圆上任一点，则为直角三角形，故球体半径，由球体表面积公式可得.‎ ‎16．在正三棱柱ABC﹣A1B1C1中，若，则AB1与C1B所成的角的大小为___________.‎ ‎【答案】900‎ ‎【解析】不妨设BB1=1，则AB=， ‎ ‎ ‎ ‎ ‎ ‎∴直线AB1与C1B所成角为90°‎ 故答案为：900.‎ 点睛：这个题目考查的是立体中异面直线的夹角的求法，常用方法是建系法，直接找两个直线的方向向量，求方向向量的夹角即可；或者将异面直线平移到同一个平面中，转化为平面直线的夹角问题。‎ 三、解答题 ‎17．在△ABC中，内角A，B，C的对边分别为a，b，c，且(2b－c)cos A＝acos C．‎ ‎(1)求角A的大小；‎ ‎(2)若a＝3，b＝2c，求△ABC的面积．‎ ‎【答案】（1）（2）‎ ‎【解析】试题分析：（1）根据已知，利用正弦定理，求出，求出角A的大小；（2）由余弦定理的推论，求出边长c，由b=2c 求出边长b，由三角形面积公式求出面积。‎ 试题解析：　(1)根据正弦定理，由(2b－c)cos A＝acos C，‎ 得2sin Bcos A＝sin Acos C＋sin Ccos A，‎ 即2sin Bcos A＝sin(A＋C)，‎ 所以2sin Bcos A＝sin B，‎ 因为0

查看更多