人教版高中数学必修二11空间几何体名师

人教版高中数学必修二11空间几何体名师

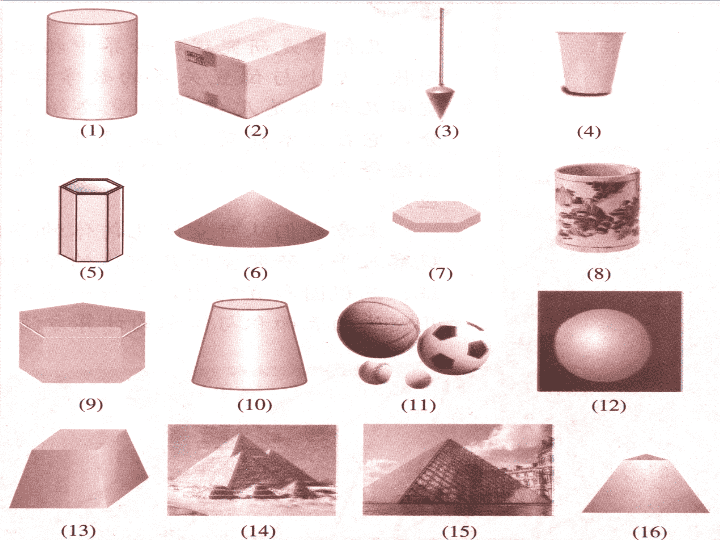
第一章： 第一部分： 空间几何体 空间几何体学习内容流程 直观认识多面体和旋转体 截面：任意截，横截，竖截，过顶点截 侧面展开图 包含最短路程 表面积和体积 直观图 面 顶点 棱 由若干个平面多边形围成的几何体叫做 多面体 . 轴 由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做 旋转体 一．多面体及相关概念 1 ．多面体： 多面体是由若干个平面多边形所围成的几何体，如下图中的几何体都是多面体 . （ 1 ）围成多面体的各个多边形叫做多面体的 面 ； （ 2 ）相邻两个面的公共边叫做多面体的 棱 ； 2 ．相关概念： A B C D A` B` C` D` 2 ．相关概念： （ 3 ）棱和棱的公共点叫做多面体的 顶点 ； （ 4 ）连接不在同一个面上的两个顶点的线段叫做多面体的 对角线 ； A B C D A` B` C` D` （ 5 ）凸、凹多面体：把一个多面体的任意一个面延展为平面，如果其余各面都在这个平面的同一侧，则这样的多面体就叫做 凸多面体 ，其他的多面体叫做 凹多面体 ； （ 6 ）截面：一个几何体和一个平面相交所得到的平面图形（包括它的内部），叫做这个几何体的 截面 ； 2 ．相关概念： 空间几何体 多面体 旋转体 棱 柱 棱 台 棱 锥 圆 柱 圆 台 圆 锥 球 体 知识框架 一 . 棱柱 1. 概念：有两个面互相平行，其余各面都是四边形，每相邻两个面交线都互相平行，由这些面围成的多面体叫做 棱柱 . 棱柱的 底面 ， 侧面 ， 侧棱 ， 顶点 . 侧面 顶点 侧棱 底面 A B C D A` B` C` D` 底 面 侧 面 侧 棱 顶点 对 角 线 高 2. 如何理解棱柱？ ① 从运动的观点来看，棱柱可以看成是一个多边形（包括图形围成的平面部分）上各点都 沿着同一个方向移动相同的距离 所经过的空间部分。 如果多边形水平放置，则移动后的多边形也水平放置。 ② 棱柱的特征： 侧棱平行且相等 侧面是平行四边形 直（正）棱柱侧面是全等的矩形 两底面及平行于底面的截面是全等的多边形 （ 1 ）按底面多边形的边数分为三棱柱、四棱柱、五棱柱等（见图） 3 ．棱柱的分类： （ 2 ）按侧棱与底面的关系分类： 侧棱与底面不垂直的棱柱叫做 斜棱柱 ； 侧棱与底面垂直的棱柱叫做 直棱柱 ； 底面是正多边形的直棱柱叫做 正棱柱 。 3 ．棱柱的分类： 4 ．棱柱的表示 ： （ 1 ）用表示 各顶点 的字母表示棱柱：如棱柱 ABCD － A 1 B 1 C 1 D 1 ； （ 2 ）用一条 对角线 端点的两个字母来表示，如棱柱 AC 1 . （ 1 ）底面是平行四边形的棱柱叫做 平行六面体 ； （ 2 ）侧棱与底面垂直的平行六面体叫做 直平行六面体 ； 5 ．特殊的四棱柱 ： 5 ．特殊的四棱柱 ： （ 3 ）底面是矩形的直平行六面体叫做 长方体 ； （ 4 ）棱长都相等的长方体叫做 正方体 . 四棱柱 平行六面体 长方体 直平行六面体 正四棱柱 正方体 底面是 平行四边形 侧棱与底面 垂直 底面是 矩形 底面为 正方形 侧棱与底面 边长相等 几种四棱柱（六面体）的关系： 思考 ： 棱柱集合、斜棱柱集合、直棱柱集合、正棱柱集合之间存在怎样的包含关系？ 斜棱柱 直棱柱 正棱柱 棱柱 思考：有两个面互相平行，其余各面都是平行四边形的多面体一定是棱柱吗？ 二：棱 锥 棱锥的底面 棱锥的侧面 棱锥的顶点 棱锥的侧棱 S A B C D E 1 、 棱锥的概念 (1) 一个面是多边形 (2) 其余各面是有一个公共顶点的三角形 2 、 棱锥的分类 ： 按底面多边形的边数，可以分为三棱锥、四棱锥、五棱锥、 …… A B C D S 3 、 棱锥的表示方法： 用表示顶点和底面的字母表示，如四棱锥 S-ABCD 。 S A B C D E O M 正棱锥 ：如果棱锥的底面是 正多边形 ，且它的顶点在过底面中心且与底面垂直的直线上，则这个棱锥叫做正棱锥。 （ 1 ） 正棱锥 4. 特殊的棱锥 正棱锥性质 1 、底面是正多边形； 2 、顶点和底面中心的连线与底面垂直； 3 、側棱长都相等； 4 、各侧面都是全等的等腰三角形； 5 、斜高都相等； 正四棱锥 V-ABCD ，底面面积为 16 ，一条側棱长为 ，由此我们可以求出哪些量？ B D C A V O M 四棱锥 V-OBM ，有几个面是直角三角形？ （ 2 ）正多面体 正四面体 四个面是全等的正三角形 正六面体 正八面体 思考： 一个三棱柱最少可以分割成几个三棱锥？ A C A 1 B B 1 C 1 A 1 B B 1 C 1 A A 1 B C 1 A C B C 1 三、棱台的结构特征 B C A D S B 1 A 1 C 1 D 1 D B C A C 1 B 1 A 1 D 1 1 、棱台的概念： 用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的部分叫做棱台。 D B C A C 1 B 1 A 1 D 1 上底面 下底面 侧面 侧棱 顶点 2 、 棱台的分类： 由三棱锥、四棱锥、五棱锥 … 截得的棱台，分别叫做 三棱台，四棱台，五棱台 … 3 、 棱台的表示法： 棱台用表示上、下底面各顶点的字母来表示，如右图， 棱台 ABCD-A 1 B 1 C 1 D 1 D B C A C 1 B 1 A 1 D 1 A B C D A 1 E 1 O 1 D 1 C 1 B 1 O E 正棱台 ：由正棱锥截得的棱台叫做正棱台 旋转体：圆柱、圆锥、圆台和球 这些几何体是如何形成的？它们的结构特征是什么？ A A ’ O O ’ 轴 底面 侧面 母线 以矩形的一边所在直线为旋转轴 , 其余边旋转形成的曲面所围成的几何体叫做圆柱。 1. 圆柱的结构特征 (1) 圆柱的形成 (2) 圆柱的结构特征 (1) 圆锥的形成 2. 圆锥的结构特征 顶点 S A B O 底面 轴 侧面 母线 以直角三角形的一条直角边所在直线为旋转轴 , 其余两边旋转形成的曲面所围成的几何体叫做圆锥。 2. 圆锥的结构特征 结构特征 O O ’ 用一个平行于圆锥底面的平面去截圆锥 , 底面与截面之间的部分是圆台 . 3. 圆台的结构特征 4. 球 的结构特征 以半圆的直径所在的直线为旋转轴，将半圆旋转所形成的曲面叫作 球面 ，球面所围成的几何体叫作 球体 ，简称 球 。 球心 半径 直径 O 想一想： 用一个平面去截一个球 , 截面是什么 ? O 用一个截面去截一个球，截面是圆面。 球面被经过球心的平面截得的圆叫做 大圆 。 球面被不过球心的截面截得的圆叫球的 小圆 。 球、圆柱、圆锥、圆台过轴的截面分别是什么图形？ 想一想： 轴截面 棱柱 棱锥 圆柱 圆锥 圆台 棱台 球 （ 1 ）棱柱与圆柱统称为柱体。 （ 2 ）棱锥与圆锥统称为锥体。 旋转体 （ 2 ）棱台与圆台统称为台体。 多面体 简单组合体： 球内有相距 1cm 的两个平行截面的面积分别是 5 cm 2 , 8cm 2 , 球心不在截面之间，求球的半径 O O 2 O 1 A B 练习 . 在球内有相距 14cm 的两个平行截面，它们的面积分别是 64πcm 2 和 36πcm 2 ，求球的半径 . . 解：设球半径为 R ， （ 1 ）当截面在球心同侧，如图（ 1 ） （ 1 ） 则有√ R 2 - 36 - √R 2 - 64=14 而此方程无解，故截面在球心的同侧 不可能。 （ 2 ）当截面在球心异侧，如图（ 2 ） （ 2 ） 则有√ R 2 - 36 + √R 2 - 64=14 解得 R=10 ∴ S 球面 =4πR 2 =400π(cm) 2 截面： 斜截，横截，竖截，过顶点截 侧面展开图 包含最短路程 截面 1 、任意截：截面形状 （正方体） 2 、平行截： 中截面 （柱锥台球） 计算点：相似比 3 、垂直截： 轴截面 （正的柱锥台） 计算点：勾股定理 4 、过顶点截： （正棱锥，圆锥） 最大面积 正方体截面形状小结 形状 特殊情形 三角形 等 腰 三 角 形 等 边 三 角 形 四边形 平 行 四 边 形 长 方 形 正 方 形 梯 形 五边形 六边形 (1) (5) 2. 平行截 中截面 H P C B D A O 截面和底面 相似 , 面积比 等于截得的棱锥的高与已知棱锥的高的 平方比 C` B` D` A` 2. 垂直截 轴截面 圆柱、圆锥、圆台轴截面 A B C D A B C A B C D 矩 形 等腰三角形 等腰梯形 直三棱柱、正三棱锥、正三棱台 C O B A P D 正四棱锥 V-ABCD ，底面面积为 16 ，一条側棱长为 ，由此我们可以求出哪些量？ B D C A V O M A B C D A 1 E 1 O 1 D 1 C 1 B 1 O E 正棱台 3. 过顶点截 侧面展开图 侧面展开图 侧面积和表面积 中心角 最短路程 展开图 长方体 正棱柱的侧面展开图 h a 侧面展开 正棱锥的侧面展开图 侧面展开 h' h' 正棱台的侧面展开图 侧面展开图 几何体的展开图 侧面 展开图的构成 一组平行四边形 一组梯形 一组三角形 正的柱锥台 圆柱、圆锥、圆台的侧面积 侧面展开图 侧面积 C’=0 C’=C S 圆柱侧 = 2πrl S 圆锥侧 = πrl S 圆台侧 =π （ r 1 +r 2 )l r 1 =0 r 1 =r 2 小结： 侧面展开图的中心角 蚂蚁爬行的最短路线 A B 最短路程 如图所示，长方体 ABCD—A 1 B 1 C 1 D 1 中， AB=a ， BC=b ， BB 1 =c ，并且 a ＞ b ＞ c ＞ 0. 求沿着长方体的表面自 A 到 C 1 的最短线路的长 . 将长方体相邻两个面展开有下列三种可能，如图所示 . 三个图形甲、乙、丙中 AC 1 的长分别为： ∵ a ＞ b ＞ c ＞ ,∴ab ＞ ac ＞ bc ＞ 0. 故最短线路的长为 . A C A 1 B B 1 C 1 D D C B1 A A A1 正三棱锥 PA=1 ， ， 过 A 点的截面周长最短为多少？ C B A P P A B C A1 【 提示 】 将所走路线形成的几个面展成一个平面 . 高考链接 直三棱柱框架 ABC-A 1 B 1 C 1 中， ∠ ACB=90°,AC=BC=CC 1 = P 是 BC 1 上一动点，则 CP+PA 1 的最小值为 . 空间几何体的体积 某长方体纸盒的长、宽、高分别为 4cm ， 3cm ， 3cm ，则每层有 __________ 个单位正方体，三层共有 ____ 个单位正方体，所以，整个长方体的体积是 _____ 4×3= 12 36 36cm 3 问题 1: 长方体体积 V 长方体 =abc 或 V 长方体 =sh (s,h 分别表示长方体的底面积和高 ) (a,b,c 分别为长方体长、宽、高 ) 取一摞书放在桌面上，并改变它们的位置，观察改变前后的体积是否发生变化？ 问题 2: 一般柱体的体积 高度、书中每页纸面积和顺序不变 1 实验猜想： 3 、祖暅原理 2 、作图验证 两 等高 的几何体 , 若在 所有等高处 的水平 截面的面积相等 ，则这两个几何体的体积相等 ． 我国古代著名数学家祖冲之在计算圆周率等问题方面有光辉的成就。祖冲之的儿子祖暅也在数学上有突出贡献。祖暅在实践的基础上，于 5 世纪末提出了这个体积计算原理。 祖暅提出这个原理，要比其他国家的数学家早一千多年。在欧洲只道 17 世纪，才有意大利数学家卡瓦列里（ Cavalieri .B ， 1598 年 --1647 年） 提出上述结论。 （ 429 年 ~500 年） 4 、 柱的体积 s h S S 底面积相等，高也相等的柱体的体积也相等。 V 柱体 =sh 1 ． 锥体（棱锥、圆锥）的体积 （底面积 S， 高 h ） 注：三棱锥的顶点和底面可根据需要变换，四面体的每一个面都可以作为底面 . 问题 3: 锥体 ( 棱锥、圆锥） 的体积 类似的 , 底面积相等 , 高也相等的两个锥 体的体积也相等 . V 锥体 = S 为底面积 ,h 为高 . s s 2 等底面积等高的锥体的体积有何关系? s s / s s / h x V 台体 = 上下底面积分别是 s / ,s, 高是 h ，则 问题 4: 台体 ( 棱锥、圆锥） 的体积 V 台体 = V 柱体 =sh V 锥体 = s s / s s / s S / =0 S=S ’ 问题 5 : 柱、锥、台的体积关系 假设在青藏铁路的某段路基需要用碎石铺垫．已知路基的形状尺寸如图所示（单位：米），问每修建 1 千米铁路需要碎石多少立方米？ 例题探究 O N P 六角螺帽毛坯，底面六边形的边长 a, 高是 b, 内孔直径是 c, 则体积为？ 2 、用一张长 12cm 、宽 8cm 的铁皮围成圆柱形的侧面，该圆柱体积为 ______ （结果保留 ） 课堂练习 1 、已知一正四棱台的上底面边长为 4cm, 下 底面边长为 8cm, 高为 3cm, 其体积为 ______ 112cm 3 3 、埃及胡夫金字塔大约建于公元前 2580 年 , 其形状为 正四棱锥 . 金字塔高 146.6 米 , 底面边长 230.4 米 . 求这座金字塔的体积 . V=2594046.0(m 3 ) R R 球的体积： 一个半径和高都等于 R 的圆柱，挖去一个 以上底面为底面，下底面圆心为顶点的圆锥 后，所得的几何体的体积与一个半径为 R 的 半球的体积相等。 R R R S 1 球的表面积： 球的表面积： 2. 一个正方体内接于半径为R的球内，求正方体的体积． 1. 一平面截一球得直径是 6cm 的圆面，球心到这个平面的距离是 4cm ，求该球的表面积和体积． 完美形 正四面体、正方体、球 内切 外接问题 正方体棱长为 a ，球半径为 R ，求下列条件下 a 与 R 的关系。 (1) 球与正方体的各个面都相切； (2) 球与正方体的各个棱都相切。 (3) 正方体的顶点都在球面上；（长方体） O O 1 A B 直角三角形：勾股定理 正四面体与球 外接 O 1 O A B 正四面体内切球半径为 R ，正四面体棱长为 a （中华画） 相似比：斜边之比 内切 A 、 B 、 C 在球面上， AC=BC=6 ， AB=4 ， 球心 O 与△ ABC 的外心 M 的距离等于球半径的一半，求球的表面积和体积 A B C O M 将一个半径为 1 的球投入底面边长是 4 的正四棱柱型盛水容器中，求水面上升的高度？ 半球的半径为 R ，一正方体的四个顶点在半球的底面上，另四个顶点在球面上，求正方体的棱长 空间几何体的 三视图和直观图 中心投影和平行投影 1. 投影 2. 中心投影 光由一点向外散射形成的投影，叫做 中心投影 ． 其投影线交于一点 ( 投影中心 ) ． 3. 平行投影 投影线为平行线时的投影称为平行投影 ． 斜投影： 投射线倾斜于投影面 ★★正投影： 投射线垂直于投影面 S 投射方向 投射方向 三角板在中心投影和不同方向的平行投影下的投影效果 平行光线 空间几何体的直观图 例１ ．用斜二测画法画水平放置的六边形的直观图 1. 用斜二测画法画水平放置平面图形的直观图 (1) 在六边形 ABCDEF 中，取 AD 所在的直线为 X 轴，对称轴 MN 所在直线为 Y 轴，两轴交于点 O ．画对应的 轴，两轴相交于点 ，使 注意： (1) 建系时要尽量考虑图形的对称性 (2) 画水平放置平面图形的关键是 确定多边形顶点的位置． ，在 轴上取 (2) 以 为中心，在 上取 以点 为中心，画 轴，并等于 ，再以 为中心，画 轴，并等于 注意： 水平放置的线段长不变，铅垂放置的线段长变为原 来的一半． 并擦去辅助线 x ’ 轴和 y ’ 轴，便获得正六边形 ABCDEF 水平放置的直观图 (3) 连接 ~ 请您总结斜二测画法画水平放置的平面图形的方法步骤 ~ 斜二测画法的步骤 (1) 在已知图形中取互相垂直的 x 轴和 y 轴，两轴相交于 O 点 . 画直观图时，把它画成对应的 x ’ 轴、 y ’ 轴，两轴交于 O ’ ，使 　　　 ，它们确定的平面表示水平平面． (2) 已知图形中平行于 x 轴或 y 轴的线段，在直观图中分别画成平行于 x’ 轴或 y’ 轴的线段． (3) 已知图形中平行于 x 轴的线段，在直观图中保持原长度不 变；平行于 y 轴的线段，长度为原来的一半． 说明 关于 水平放置的 圆 的直观图 的画法，常用正等测画法．在实际画水平放置的圆的直观图时，通常使用椭圆模版． 练习 P21)1,2,3 例 2 ． 用 斜二测画法 画长 , 宽 , 高分别是 4cm,3cm,2cm 的长方体的直观图 2. 用斜二测画法画空间几何体的直观图 联想水平放置的平面图形的画法，并注意到高的处理 4 1.5 例 3 ． 已知几何体的三视图，用斜二测画法画出它的直观图 · · · · · · 正视图 侧视图 俯视图 练习 P21)4,5 三视图从细节上刻画了空间几何体的结构 , 根据三视图，我们可以得到一个精确的空间几何体 , 正是因为这个特点，使它在生产活动中得到广泛应用 ( 比如零件图纸、建筑图纸等 ). 直观图是对空间几何体的整体刻画，我们可以根据直观图的结构想象实物的形象． 小结 投影 视图 中心投影 平行投影 投影线交于一点 投影线平行 正投影 斜投影 直观强、接近实物 不改变原物形状 直观图 斜二测画法 可以根据直观图的结构想象实物的形象