四川省遂宁市2019-2020学年高一下学期期末考试数学试卷 Word版含答案

四川省遂宁市2019-2020学年高一下学期期末考试数学试卷 Word版含答案

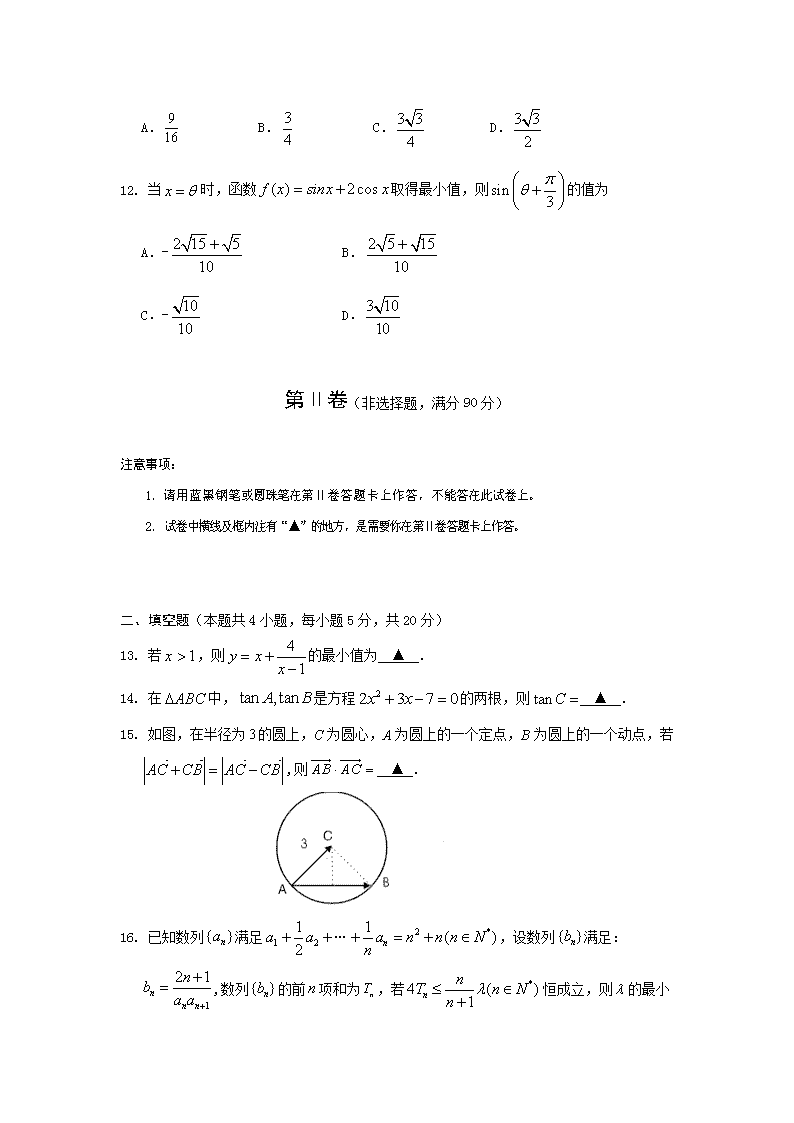
‎____________________________________________________________________________________________‎ ‎ 遂宁市高中2022届第二学期期末教学水平监测 数 学 试 题 本试卷分第I卷（选择题）和第II卷（非选择题）两部分。总分150分。考试时间120分钟。‎ 第Ⅰ卷（选择题，满分60分）‎ 注意事项：‎ ‎1．答题前，考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上。并检查条形码粘贴是否正确。‎ ‎2．选择题使用2B铅笔填涂在答题卡对应题目标号的位置上，非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。‎ ‎3．考试结束后，将答题卡收回。‎ 一、选择题（本大题共12小题，每题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求）‎ ‎1. 现有这么一列数：1，，，，（ ），，，…，按照规律，（ ）中的数应为 A． B． C． D．‎ ‎2. 设，且，则 A. B. ‎ C. D. ‎ ‎3. 在△ABC中，点D在边BC上，若，则 A. B. ‎ C. D. ‎ ‎____________________________________________________________________________________________‎ ‎4. 设单位向量，则的值为 A． B． C． D．‎ ‎5. 已知△ABC中，，那么满足条件的△ABC ‎ A．有一个解 B．有两个解 C．不能确定 D．无解 ‎6. 已知数列成等差数列，成等比数列，则的值是 ‎ A．或 B． C． D．‎ ‎7. 《九章算术》是我国古代内容极为丰富的一部数学专著，书中有如下问题：今有女子善织，日增等尺，七日织28尺，第二日，第五日，第八日所织之和为15尺，则第十四日所织尺数为 A．13 B．14 ‎ C．15 D．16‎ ‎8．在△ABC中，角A、B、C的对边分别为a、b、c，其中，‎ 那么△ABC一定是 A. 锐角三角形 B. 直角三角形 ‎ ‎ C. 等腰三角形 D. 等腰或直角三角形 ‎9．已知，都是锐角，，，则 A． B． C． D．‎ ‎10．如图所示，隔河可以看到对岸两目标AB，但不能到达，现在岸边取 相距‎4km的C，D两点，测得∠ACB＝75°,∠BCD＝45°,∠ADC＝30°,∠ADB＝45°(A，B，C，D在同一平面内)，则两目标A，B间的距离为( )km.‎ A．2 B． C． D．‎ ‎11. 设是△ABC的重心，且，若△ABC外接圆的半径为1，则△ABC的面积为 ‎____________________________________________________________________________________________‎ A． B． C． D．‎ ‎12. 当时，函数取得最小值，则的值为 A．- B． ‎ ‎ C．- D．‎ 第Ⅱ卷（非选择题，满分90分）‎ 注意事项：‎ ‎1．请用蓝黑钢笔或圆珠笔在第Ⅱ卷答题卡上作答，不能答在此试卷上。‎ ‎2．试卷中横线及框内注有“▲”的地方，是需要你在第Ⅱ卷答题卡上作答。‎ 二、填空题（本题共4小题，每小题5分，共20分）‎ ‎13. 若，则的最小值为 ▲ ．‎ ‎14. 在中，是方程的两根，则 ▲ ．‎ ‎15. 如图，在半径为的圆上，C为圆心，A为圆上的一个定点，B为圆上的一个动点，若,则 ▲ ．]‎ ‎:Z#xx#‎ ‎.Com]‎ ‎16. 已知数列满足…，设数列满足：,数列的前项和为，若恒成立，则 ‎____________________________________________________________________________________________‎ 的最小值是 ▲ ．‎ 三、解答题：解答应写出必要的文字说明、证明过程或演算步骤.‎ ‎17．（本小题满分10分）‎ 已知□ABCD的三个顶点A、B、C的坐标分别是（-2,1）、（-1,3)、(3,4).‎ ‎（1）求顶点D的坐标；‎ ‎（2）求与所成夹角的余弦值．‎ ‎▲‎ ‎18．（本小题满分12分）‎ 已知数列是公比为2的等比数列，且成等差数列． ‎ ‎（1）求数列的通项公式； ‎ ‎（2）记，数列的前项和为，求．‎ ‎▲‎ ‎19．（本小题满分12分）‎ 已知向量，且函数.‎ ‎（1）求函数在时的值域；‎ ‎（2）设是第一象限角，且求的值.‎ ‎▲‎ ‎20．（本小题满分12分）‎ 首届世界低碳经济大会‎11月17日在南昌召开，本届大会的主题为“节能减排，绿色生态”‎ ‎____________________________________________________________________________________________‎ ‎.某企业在国家科研部门的支持下，投资810万元生产并经营共享单车，第一年维护费为10万元，以后每年增加20万元，每年收入租金300万元.‎ ‎（1）若扣除投资和各种维护费，则从第几年开始获取纯利润？‎ ‎（2）若干年后企业为了投资其他项目，有两种处理方案：‎ ‎①纯利润总和最大时，以100万元转让经营权；‎ ‎②年平均利润最大时以460万元转让经营权，问哪种方案更优？‎ ‎▲‎ 21． ‎（本小题满分12分）‎ 已知的角A,B,C的对边分别为a,b,c,满足.‎ ‎（1）求A;‎ ‎（2）从下列条件中:①；②中任选一个作为已知条件，求周长的取值范围.‎ ‎ 注：如果选择多个条件分别解答，按第一个解答计分.‎ ‎▲‎ 22． ‎（本小题满分12分）‎ 函数满足：对任意，都有，且，数列满足.‎ ‎（1）证明数列为等差数列，并求数列的通项公式；‎ ‎（2）记数列前n项和为，且，问是否存在正整数m，使得成立，若存在，求m的最小值 ；若不存在， 请说明理由.‎ ‎▲‎ ‎____________________________________________________________________________________________‎ 遂宁市高中2022届第二学期期末教学水平监测 数学试题参考答案及评分意见 一、选择题（本大题共12小题，每题5分，共60分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A C B C B C B D D C C A 二、填空题(本大题共4小题，每小题5分，共20分)‎ ‎13．5 14． 15．9 16． ‎ 三、解答题 ‎17．（本小题满分10分）‎ 解：（1）设顶点D的坐标为．‎ ‎，，，‎ ‎，， --------------------2分 又， --------------------3分 所以．即解得 所以顶点D的坐标为． --------------------5分 ‎（2）由 ‎ ‎ ‎ --------------------8分 ‎ --------------------10分 ‎18．（本小题满分12分）‎ ‎____________________________________________________________________________________________‎ ‎（1）由题意可得， --------------------2分 即，解得：，∴， --------------------4分 ‎∴数列的通项公式为． -------------------6分 ‎（2） --------------------7分 ‎ --------------------10分 ‎ --------------------12分 ‎19．（本小题满分12分）‎ 解：(1)由 --------------------1分 ‎ -----------------3分 ‎ -----------------5分 所以的值域为 -----------------6分 ‎（2）‎ 则即 又为第一象限的角则 ----------------9分 ‎ ----------------10分 ‎ -----------------12分 ‎20．（本小题满分12分）‎ ‎____________________________________________________________________________________________‎ 解：（1）设第年获取利润为y万元，年共收入租金万元，付出维护费构成一个以10为首项，20为公差的等差数列，共 -----------------2分 因此利润 -------------------3分 令，解得：‎ 所以从第4年开始获取纯利润． -----------------5分 ‎（2）方案①：纯利润 所以15年后共获利润：1440+100=1540（万元） -----------------8分 方案②：年平均利润 当且仅当，即n=9时取等号 所以9年后共获利润：120×9+460=1540（万元） -----------------11分 综上：两种方案获利一样多，而方案②时间比较短，所以选择方案②． ------------12分 ‎21．（本小题满分12分）‎ 解：（1）因为 由正弦定理得，即 -----------------2分 由余弦定理得 -----------------4分 所以 -----------------5分 （2） 选择①.由正弦定理， -----------------6分 即周长 ‎ ‎ ‎____________________________________________________________________________________________‎ ‎ ----------------9分 ‎ ----------------11分 即周长的取值范围 ----------------12分 选择②.,得,得. ----------------7分 由余弦定理得 ----------------9分 即周长 ‎,当且仅当时等号成立. ----------------11分 即周长的取值范围 ----------------12分 ‎22．（本小题满分12分）‎ 解：‎ ‎, ----------------2分 ‎ ‎ 为等差数列，首项为，公差为1， ----------------4分 ‎. ----------------5分 ‎（2）由 ----------------6分 ‎ ‎ ‎____________________________________________________________________________________________‎ ‎, 两式相减得 ‎ ‎ ‎ ‎ -----------------9分 假设存在正整数，使得成立，即---------10分 由指数函数与一次函数单调性知： 为增函数.‎ 又因为 -------------11分 所以当时恒有成立.‎ 故存在正整数,使得成立，的最小值为4. ---------12分 ‎ …………12分