变量之间的相关关系教案2

变量之间的相关关系教案2

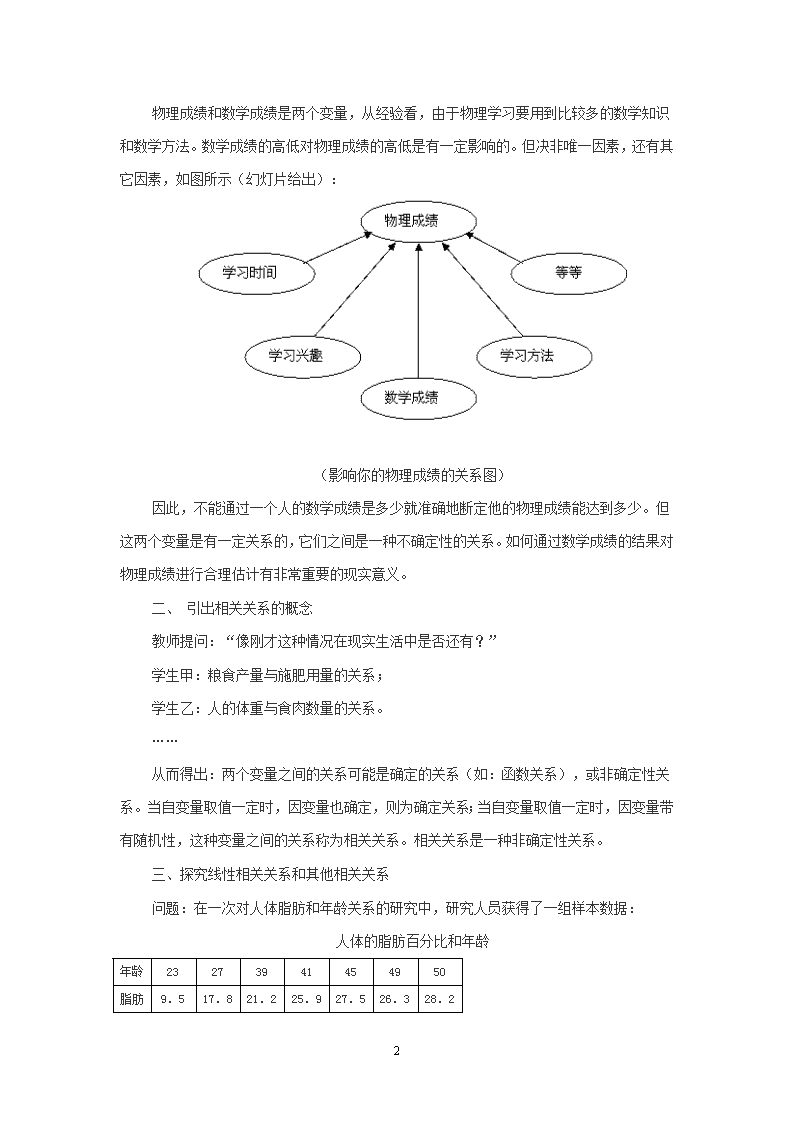
‎ ‎ 变量间的相关关系的教学设计 本节教学设计主要是使用TI92图形计算器，对普通高中课程标准实验教科书数学③第二章《统计》中的“两个变量的线性相关”进行有益的教与学探究。学生通过对 TI图形计算器的操作，具体形象地利用散点图等直观图形认识变量之间的相关关系，同时，经历描述两个变量的相关关系的过程。学生亲自体验了发现数学、领悟数学的全过程。与此同时，教师在落实新课程标准的相关理念上作了一些有益的探讨。‎ 教学设计与实践：‎ ‎[教学目标]：‎ ‎1、 明确事物间的相互联系。认识现实生活中变量间除了存在确定的关系外，仍存在大量的非确定性的相关关系，并利用散点图直观体会这种相关关系。‎ ‎2、 通过TI技术探究用不同的估算方法描述两个变量的线性相关关系的过程，学会用数学的有关变量来描述现实关系。‎ ‎3、知道最小二乘法思想，了解其公式的推导。会用TI图形计算器来求回归方程，相关系数。‎ ‎[教学用具]：‎ 学生每人一台TI图形计算器、多媒体展示台、幻灯 ‎[教学实践情况]：‎ 一、 问题引出：请同学们如实填写下表（在空格中打“√” ）‎ ‎ ‎ 好 中 差 你的数学成绩 ‎ ‎ ‎ ‎ ‎ ‎ 你的物理成绩 ‎ ‎ ‎ ‎ ‎ ‎ ‎   然后回答如下问题：①“你的数学成绩对你的物理成绩有无影响？”②“ 如果你的数学成绩好，那么你的物理成绩也不会太差，如果你的数学成绩差，那么你的物理成绩也不会太好。”对你来说，是这样吗？同意这种说法的同学请举手。‎ 根据同学们回答的结果，让学生讨论：我们可以发现自己的数学成绩和物理成绩存在某种关系。（似乎就是数学好的，物理也好；数学差的，物理也差，但又不全对。）教师总结如下：‎ 14‎ ‎ ‎ 物理成绩和数学成绩是两个变量，从经验看，由于物理学习要用到比较多的数学知识和数学方法。数学成绩的高低对物理成绩的高低是有一定影响的。但决非唯一因素，还有其它因素，如图所示（幻灯片给出）：‎ ‎ ‎ ‎（影响你的物理成绩的关系图）‎ 因此，不能通过一个人的数学成绩是多少就准确地断定他的物理成绩能达到多少。但这两个变量是有一定关系的，它们之间是一种不确定性的关系。如何通过数学成绩的结果对物理成绩进行合理估计有非常重要的现实意义。‎ 二、 引出相关关系的概念 教师提问：“像刚才这种情况在现实生活中是否还有？”‎ 学生甲：粮食产量与施肥用量的关系；‎ 学生乙：人的体重与食肉数量的关系。‎ ‎……‎ 从而得出：两个变量之间的关系可能是确定的关系（如：函数关系），或非确定性关系。当自变量取值一定时，因变量也确定，则为确定关系；当自变量取值一定时，因变量带有随机性，这种变量之间的关系称为相关关系。相关关系是一种非确定性关系。‎ 三、探究线性相关关系和其他相关关系 问题：在一次对人体脂肪和年龄关系的研究中，研究人员获得了一组样本数据：‎ 人体的脂肪百分比和年龄 年龄 ‎23‎ ‎27‎ ‎39‎ ‎41‎ ‎45‎ ‎49‎ ‎50‎ 脂肪 ‎9．5‎ ‎17．8‎ ‎21．2‎ ‎25．9‎ ‎27．5‎ ‎26．3‎ ‎28．2‎ 14‎ ‎ ‎ ‎ ‎ 年龄 ‎53‎ ‎54‎ ‎56‎ ‎57‎ ‎58‎ ‎60‎ ‎61‎ 脂肪 ‎29．6‎ ‎30．2‎ ‎31．4‎ ‎30．8‎ ‎33．5‎ ‎35．2‎ ‎34．6‎ 针对于上述数据所提供的信息，你认为人体的脂肪含量与年龄之间有怎样的关系？教师特别向学生强调在研究两个变量之间是否存在某种关系时，必须从散点图入手（向学生介绍什么是散点图）。并且引导学生从散点图上可以得出如下规律：（幻灯片给出）‎ ‎1、如果所有的样本点都落在某一函数曲线上，那么变量之间具有函数关系（确定性关系）；‎ ‎2、如果所有的样本点都落在某一函数曲线的附近，那么变量之间具有相关关系（不确定性关系）；‎ ‎3、如果所有的样本点都落在某一直线附近，那么变量之间具有线性相关关系（不确定性关系）。‎ 下面我们用TI图形计算器作出这两个变量的散点图。‎ 学生实验：先把数据中成对出现的两个数分别作为横坐标、纵坐标，把数据输入到表格当中（第一列横坐标、第二列纵坐标）得到图1；然后，用TI图形计算器作散点图得图2：‎ ‎（图1）‎ ‎ （图2）‎ 引导学生观察作出的散点图，体会现实生活中两个变量之间的关系存在着不确定性。散点图中的散点并不在一条直线上，只是分布在一条直线的周围，即为线性相关关系。‎ 14‎ ‎ ‎ 给出三组数据（表1-3），请学生作出散点图，并观察每组数据的特点。‎ 表1：‎ ‎-5‎ ‎0‎ ‎4‎ ‎7‎ ‎12‎ ‎15‎ ‎19‎ ‎23‎ ‎27‎ ‎31‎ ‎36‎ ‎156‎ ‎150‎ ‎132‎ ‎128‎ ‎130‎ ‎116‎ ‎104‎ ‎89‎ ‎93‎ ‎76‎ ‎54‎ 表2 ： ‎ ‎-12‎ ‎-9‎ ‎-5‎ ‎-4‎ ‎-3‎ ‎-1‎ ‎0‎ ‎2‎ ‎4‎ ‎6‎ ‎9‎ ‎13‎ ‎120‎ ‎100‎ ‎20‎ ‎12‎ ‎6‎ ‎2‎ ‎0‎ ‎3.5‎ ‎23‎ ‎27‎ ‎70‎ ‎150‎ 表3：‎ ‎-9‎ ‎-7‎ ‎-5‎ ‎-4‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎3‎ ‎5‎ ‎7‎ ‎9‎ ‎1/560‎ ‎1/100‎ ‎1/30‎ ‎1/18‎ ‎1/5‎ ‎9/10‎ ‎10/11‎ ‎3‎ ‎9‎ ‎28‎ ‎100‎ ‎550‎ 表4：‎ ‎-13‎ ‎-11‎ ‎-9‎ ‎-7‎ ‎-5‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎3‎ ‎4‎ ‎5‎ ‎92‎ ‎55‎ ‎31‎ ‎15‎ ‎6‎ ‎5‎ ‎9‎ ‎12‎ ‎19‎ ‎30‎ ‎50‎ ‎70‎ ‎88‎ 根据表1-4，学生作出如下散点图，（图3、图4、图5、图6）：‎ ‎　　　　　　　‎ ‎ （图3）　　　　　　　　　　　　　　　　　　　 （图4）‎ 14‎ ‎ ‎ ‎　　　　　　　　‎ ‎ （图5）　　　　　　　　　　　　　　　　　　　　 （图6）‎ 通过学生讨论、交流、用TI图形计算器展示、对比自己作出的散点图，我们引出线性相关关系，正负相关关系的概念。‎ 四、引出回归直线的概念，探索求回归直线方程的方法 再看图2，你能说说人在62、63、64岁时的脂肪含量大约是多少吗？‎ 通过用TI图形计算器图象，猜想：所有的点都大致分布在一条直线的附近，只要求出这条直线的方程，那么就可以知道人在62、63、64岁时的脂肪含量。如图7，从整体上看，散点图中的点分布大致在一条直线附近，我们把这条直线叫做“回归直线”。‎ ‎ （图7）‎ 14‎ ‎ ‎ 注：“回归”这个词是有英国著名的统计学家 Francils Galton 提出来的。1889年，他在研究祖先与后代身高之间的关系时发现，身材较高的父母，他们的孩子也较高，但这些孩子的平均身高并没有他们的父母平均身高高；身材较矮的父母，他们的孩子也较矮，但这些孩子的平均身高却比他们的父母平均身高高。Galton 把这种后代的身高向中间值靠近的趋势称为“回归现象”。后来，人们把由一个变量的变化去推测另一个变量的变化的方法称为“回归方法”。‎ 那么如何求回归直线方程呢？人们在思考这个问题的时候，常用以下3种方法：‎ ‎1、采用测量的方法，先画一条直线，测量出各点到它的距离，然后移动直线，到达一个使距离之和最小的位置，测量出此时直线的斜率和截距，就得到回归方程。‎ ‎2、在图中选取两点画直线，使得直线两侧的点的个数基本相同。‎ ‎3、在散点图中多取几个点，确定几条直线的方程，分别求出各条直线的斜率和截距的平均数，将这两个平均数作为回归方程的斜率和截距。‎ 上面的这些方法虽然有一定的道理，但总让人感觉到可靠性不强。统计学中，科学家们经过研究后于是得出了如下方法：求回归方程的关键是如何用数学的方法来刻画“从整体上看各点与此直线的距离和最小”。现在，我们来看一下数学家解决这个问题的思维过程吧。‎ 设已经得到具有线性相关关系的一组数据：，所要求的回归直线方程为：，其中，是待定的系数。当变量取时，可以得到。求的最小值，其步骤为：‎ 14‎ ‎ ‎ 最后，指导学生直接利用TI图形计算器，计算人的脂肪含量与年龄这一问题。得到图8：‎ ‎（图8）‎ 五、相关系数及其含义 14‎ ‎ ‎ 从图象和回归方程可知：人的脂肪含量与人的年龄是正相关关系，那么人的年龄多大程度上决定人体的脂肪含量？这就是相关强弱的问题。如何解决这一问题，统计学家们引进相关系数这一概念，用相关系数来衡量两个变量之间的线性关系的强弱。若相应于变量的取值，变量的观测值为，‎ 则两个变量的相关系数的计算公式为： ‎ 相关关系的强弱给出具体的判断标准：首先的符号决定正、负相关关系；当时，相关关系很强；当时，相关关系一般；此外，相关关系很弱或者几乎不能用线性相关来描述。TI图形计算器结果中出现的就是相关系数，就是。‎ 通过计算，我们得到探究问题中的（如图8所示），所以我们说人的脂肪含量与人的年龄正相关关系很强。‎ 最后，我们得到问题的主要结论：‎ ‎1、 人体的脂肪与年龄之间是线性相关关系，而且正相关关系很强（ ）。‎ ‎2、这种相关关系可以用回归方程：来刻画。‎ ‎3、人在62、63、64岁时，人体的脂肪含量百分比大约为：35.26、35.84、36.42。‎ ‎[效果与回收]：‎ 一、课外实践：（用TI图形计算器等工具完成下列问题）‎ ‎1、一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了10次试验，收集数据如下：‎ 零件(个数)‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ ‎70‎ ‎80‎ ‎90‎ ‎100‎ 14‎ ‎ ‎ 加工时间（min）‎ ‎62‎ ‎68‎ ‎75‎ ‎81‎ ‎89‎ ‎95‎ ‎102‎ ‎108‎ ‎115‎ ‎122‎ ‎(1)、画出散点图；‎ ‎(2)、求回归方程；‎ ‎(3)、关于加工零件的个数与加工时间，你能得出什么结论？‎ ‎2、某机构曾研究对翻车鱼的影响。在一定温度下，经单位时间，翻车鱼的存活的比例为，数据如下：‎ ‎(0.10,1.00), (0.15,0.95), (0.20,0.95), (0.25,0.90), (0.30,0.85),‎ ‎(0.35,0.70), (0.40,0.65), (0.45,0.60), (0.50,0.55), (0.55,0.40).‎ ‎(1)、请作出这些数据的散点图；‎ ‎(2)、关于这两个变量的关系，你能得出什么结论？‎ ‎3、经过抽样，我校的部分学生的第二次段考语文和数学成绩如下：‎ 语文 ‎ ‎56‎ ‎60‎ ‎66‎ ‎70‎ ‎93‎ ‎102‎ ‎112‎ ‎115‎ ‎119‎ ‎120‎ ‎122‎ ‎126‎ 数学 ‎ ‎99‎ ‎55‎ ‎49‎ ‎124‎ ‎138‎ ‎100‎ ‎86‎ ‎91‎ ‎70‎ ‎110‎ ‎99‎ ‎82‎ ‎(1)、请作出这些数据的散点图；‎ ‎(2)、关于学生的数学成绩与语文成绩之间的关系，你能得出什么结论？‎ 二、学生完成情况综述 ‎（1）、正确的作图与结论：‎ ‎①第1题解答：‎ 14‎ ‎ ‎ ‎                ‎ ‎（图9）                                        （图10） ‎ 结论：‎ ‎1、散点图如上图9所示（已经添加了回归直线）。‎ ‎2、回归方程：。‎ ‎3、通过观察图9可知：加工零件的个数与加工时间之间是线性相关关系。因为，相关系数是：，所以，正相关关系很强。‎ ‎②第2题解答：‎ 14‎ ‎ ‎ ‎             ‎ ‎（图11）                                      （图12）‎ 结论：‎ ‎1、散点图如上图11所示（已经添加了回归直线）。‎ ‎2、回归方程：。‎ ‎3、通过观察图11可知：翻车鱼的存活的比例与单位时间之间是线性相关关系。因为，相关系数是：，所以，负相关关系很强。‎ ‎③第3题解答：‎ 14‎ ‎ ‎ ‎                ‎ ‎（图13）                                       （图14）‎ 结论：‎ ‎1、散点图如上图13所示。‎ ‎2、通过观察图13可知：学生的数学成绩与语文成绩之间的关系是不确定关系。因为，相关系数是：，所以，相关关系很弱，几乎没有线性相关关系。‎ ‎（2）、作图中存在的错误与不足：‎ 14‎ ‎ ‎ ‎             ‎ ‎（图15）                                     （图16）              ‎ ‎（图17）                                       （图18）‎ 以上的两个图形的错误或不足之处分别在于：‎ ‎①出现图15 的现象，是因为图象显示的窗口没有调整到最合适窗口。‎ 14‎ ‎ ‎ ‎②出现图16的现象，是因为在求回归直线方程过程中，按错了键，以致求出的是中位数回归方程。‎ ‎③出现图17、18的现象，是因为在求回归直线方程过程中，把数组中的的顺序颠倒了。虽然图17与图9很相近，但是，实质上是错误的作图，这一点可以从求出的回归方程（图18）：与正确的方程：相比较得到证实。‎ 14‎