2020年高考真题+高考模拟题 专项版解析汇编 文科数学——02 函数的概念与基本初等函数I(教师版)
专题02 函数的概念与基本初等函数I
1.【2020年高考全国Ⅰ卷文数】设,则
A. B. C. D.
【答案】B
【解析】由可得,所以,
所以有,
故选:B.
【点睛】本题考查的是有关指对式的运算的问题,涉及到的知识点有对数的运算法则,指数的运算法则,属于基础题目.
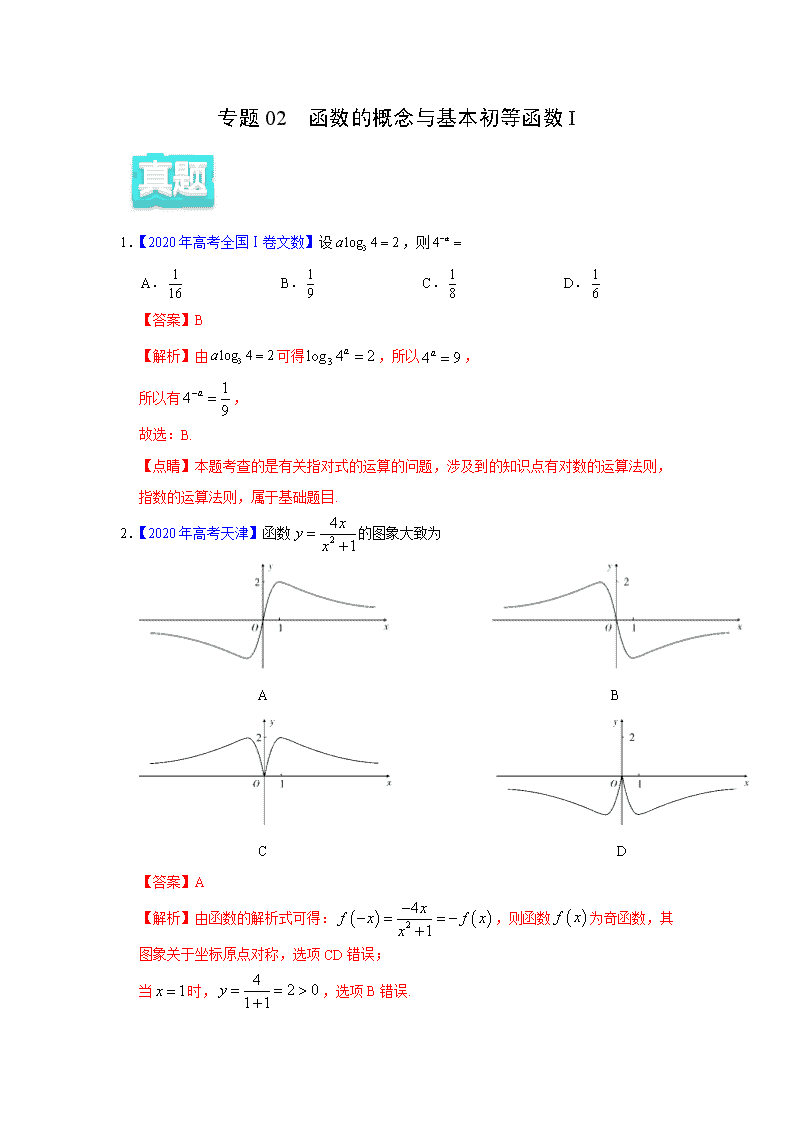
2.【2020年高考天津】函数的图象大致为
A B
C D
【答案】A
【解析】由函数的解析式可得:,则函数为奇函数,其图象关于坐标原点对称,选项CD错误;
当时,,选项B错误.
故选:A.
【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.
3.【2020年高考全国Ⅱ卷文数】在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成1200份订单的配货,由于订单量大幅增加,导致订单积压.为解决困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货,预计第二天的新订单超过1600份的概率为0.05.志愿者每人每天能完成50份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至少需要志愿者
A.10名 B.18名 C.24名 D.32名
【答案】B
【解析】由题意,第二天新增订单数为,设需要志愿者x名,
,,故需要志愿者名.
故选:B
【点晴】本题主要考查函数模型的简单应用,属于基础题.
4.【2020年高考全国Ⅲ卷文数】Logistic模型是常用数学模型之一,可应用于流行病学领城.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:,其中K为最大确诊病例数.当I()=0.95K时,标志着已初步遏制疫情,则约为(ln19≈3)
A.60 B.63 C.66 D.69
【答案】C
【解析】,所以,则,
所以,,解得.
故选:C.
【点睛】本题考查对数的运算,考查指数与对数的互化,考查计算能力,属于中等题.
5.【2020年高考全国Ⅲ卷文数】设a=log32,b=log53,c=,则
A.a
0 B.ln(y−x+1)<0
C.ln|x−y|>0 D.ln|x−y|<0
【答案】A
【解析】由得:,
令,
为上的增函数,为上的减函数,为上的增函数,
,
,,,则A正确,B错误;
与的大小不确定,故CD无法确定.
故选:A.
【点睛】本题考查对数式的大小的判断问题,解题关键是能够通过构造函数的方式,利用函数的单调性得到的大小关系,考查了转化与化归的数学思想.
8.【2020年高考天津】设,则的大小关系为
A. B. C. D.
【答案】D
【解析】因为,
,
,
所以.
故选:D.
【点睛】本题考查的是有关指数幂和对数值的比较大小问题,在解题的过程中,注意应用指数函数和对数函数的单调性,确定其对应值的范围.
比较指对幂形式的数的大小关系,常用方法:
(1)利用指数函数的单调性:,当时,函数递增;当时,函数递减;
(2)利用对数函数的单调性:,当时,函数递增;当时,函数递减;
(3)借助于中间值,例如:0或1等.
9.【2020年新高考全国Ⅰ卷】基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.
在新冠肺炎疫情初始阶段,可以用指数模型:描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69)
A.1.2天 B.1.8天
C.2.5天 D.3.5天
【答案】B
【解析】因为,,,所以,所以,
设在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间为天,
则,所以,所以,
所以天.
故选:B.
【点睛】本题考查了指数型函数模型的应用,考查了指数式化对数式,属于基础题.
10.【2020年新高考全国Ⅰ卷】若定义在的奇函数f(x)在单调递减,且f(2)=0,则满足的x的取值范围是
A. B.
C. .
【答案】D
【解析】因为定义在上的奇函数在上单调递减,且,
所以在上也是单调递减,且,,
所以当时,,当时,,
所以由可得:
或或
解得或,
所以满足的的取值范围是,
故选:D.
【点睛】本题考查利用函数奇偶性与单调性解抽象函数不等式,考查分类讨论思想方法,属中档题.
11.【2020年新高考全国Ⅰ卷】信息熵是信息论中的一个重要概念.设随机变量X所有可能的取值为,且,定义X的信息熵.
A.若n=1,则H(X)=0
B.若n=2,则H(X)随着的增大而增大
C.若,则H(X)随着n的增大而增大
D.若n=2m,随机变量Y所有可能的取值为,且,则H(X)≤H(Y)
【答案】AC
【解析】对于A选项,若,则,所以,所以A选项正确.
对于B选项,若,则,,
所以,
当时,,
当时,,
两者相等,所以B选项错误.
对于C选项,若,则
,
则随着的增大而增大,所以C选项正确.
对于D选项,若,随机变量的所有可能的取值为,且().
.
.
由于,所以,
所以,
所以,
所以,所以D选项错误.
故选:AC
【点睛】本小题主要考查对新定义“信息熵”的理解和运用,考查分析、思考和解决问题的能力,涉及对数运算和对数函数及不等式的基本性质的运用,属于难题.
12.【2020年高考天津】已知函数若函数恰有4个零点,则的取值范围是
A. B.
C. D.
【答案】D
【解析】注意到,所以要使恰有4个零点,只需方程恰有3个实根
即可,
令,即与的图象有个不同交点.
因为,
当时,此时,如图1,与有个不同交点,不满足题意;
当时,如图2,此时与恒有个不同交点,满足题意;
当时,如图3,当与相切时,联立方程得,
令得,解得(负值舍去),所以.
综上,的取值范围为.
故选:D.
【点晴】本题主要考查函数与方程的应用,考查数形结合思想,转化与化归思想,是一道中档题.
13.【2020年高考北京】已知函数,则不等式的解集是
A. B.
C. D.
【答案】D
【解析】因为,所以等价于,
在同一直角坐标系中作出和的图象如图:
两函数图象的交点坐标为,
不等式的解为或.
所以不等式的解集为:.
故选:D.
【点睛】本题考查了图象法解不等式,属于基础题.
14.【2020年高考浙江】函数y=xcos x+sin x在区间[–π,π]上的图象可能是
【答案】A
【解析】因为,则,
即题中所给的函数为奇函数,函数图象关于坐标原点对称,
据此可知选项CD错误;
且时,,据此可知选项B错误.
故选:A.
【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.
15.【2020年高考浙江】已知a,bR且ab≠0,对于任意x≥0均有(x–a)(x–b)(x–2a–b)≥0,则
A.a<0 B.a>0 C.b<0 D.b>0
【答案】C
【解析】因为,所以且,设,则零点
为
当时,则,,
要使,必有,且,
即,且,所以;
当时,则,,要使,必有.
综上一定有.
故选:C
【点晴】本题主要考查三次函数在给定区间上恒成立问题,考查学生分类讨论思想,是一道中档题.
16.【2020年高考江苏】已知y=f(x)是奇函数,当x≥0时,,则的值是 ▲ .
【答案】
【解析】,
因为为奇函数,所以
故答案为:
【点睛】本题考查根据奇函数性质求函数值,考查基本分析求解能力,属基础题.
17.【2020年高考北京】函数的定义域是____________.
【答案】
【解析】由题意得,
故答案为:
【点睛】本题考查函数定义域,考查基本分析求解能力,属基础题.
1.【2020·北京高三月考】已知函数满足,且,则
A.16 B.8 C.4 D.2
【答案】B
【解析】因为,且,故,解得.
故选B.
【点睛】本题主要考查了根据函数性质求解函数值的问题,属于基础题.
2.【2020·宜宾市叙州区第二中学校高三一模(文)】已知函数,则
A. B. C. D.
【答案】A
【解析】依题意,.
故选A.
【点睛】本小题主要考查根据分段函数解析式求函数值,属于基础题.
3.【安徽省2020届高三名校高考冲刺模拟卷数学(文科)试题】已知,则
A.a
查看更多