四川省成都龙泉驿区2013届高三 5月数学学科押题试卷（理）

四川省成都龙泉驿区2013届高三 5月数学学科押题试卷（理）

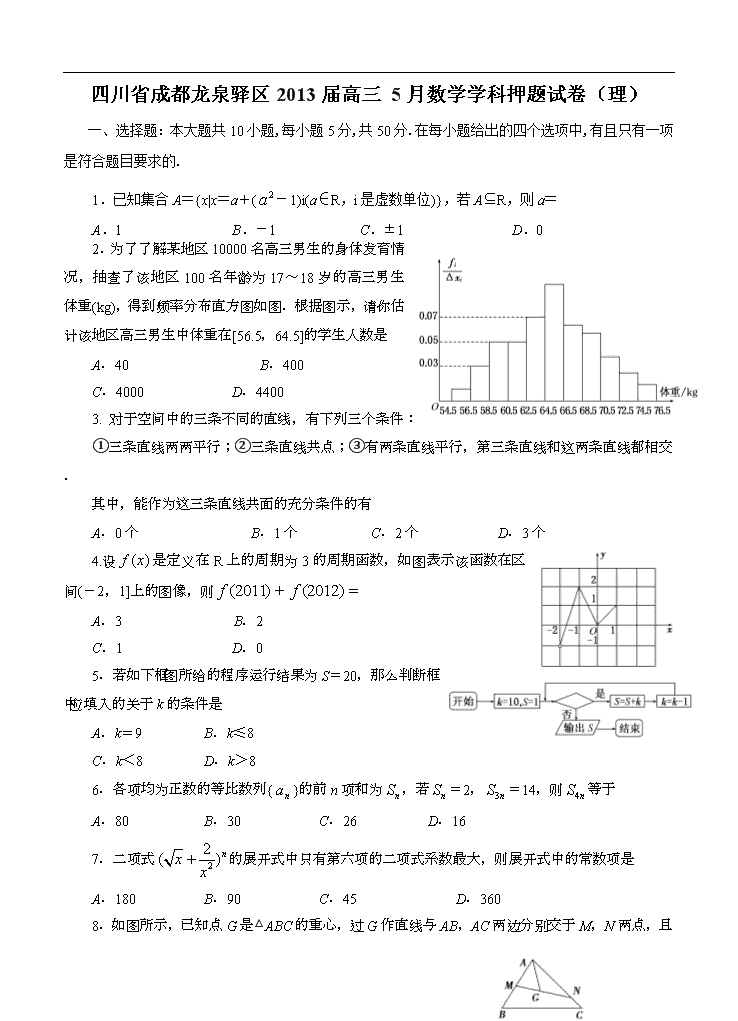
四川省成都龙泉驿区2013届高三 5月数学学科押题试卷（理）‎ 一、选择题：本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,有且 只有一项是符合题目要求的.‎ ‎1．已知集合A＝{x|x＝a＋(－1)i(a∈R，i是虚数单位)}，若A⊆R，则a＝‎ A．1 B．－‎1 ‎‎ C．±1 D．0‎ ‎2．为了了解某地区10000名高三男生的身体发育情况，抽查了该地区100名年龄为17～18岁的高三男生体重(kg)，得到频率分布直方图如图．根据图示，请你估计该地区高三男生中体重在[56.5，64.5]的学生人数是 A．40　　　　　　　　 B．400‎ C．4000 D．4400‎ ‎3. 对于空间中的三条不同的直线，有下列三个条件：‎ ‎①三条直线两两平行；②三条直线共点；③有两条直线平行，第三条直线和这两条直线都相交．‎ 其中，能作为这三条直线共面的充分条件的有 A．0个　　　　　　　　B．1个 C．2个 D．3个 ‎4.设是定义在R上的周期为3的周期函数，如图表示该函数在区间(－2，1]上的图像，则＋＝‎ A．3　　　　　　　　B．2‎ C．1 D．0‎ ‎5．若如下框图所给的程序运行结果为S＝20，那么判断框中应填入的关于k的条件是 A．k＝9 B．k≤8‎ C．k＜8 D．k＞8‎ ‎6．各项均为正数的等比数列{}的前n项和为，若＝2，＝14，则等于 A．80 B．‎30 ‎‎ C．26 D．16‎ ‎7．二项式的展开式中只有第六项的二项式系数最大，则展开式中的常数项是 A．180 B．‎90 ‎‎ C．45 D．360‎ ‎8．如图所示，已知点G是△ABC的重心，过G作直线与AB，AC两边分别交于M，N两点，且 ‎＝，＝，则的值为 A．3 B. C．2 D.‎ ‎9．已知抛物线C的方程为＝，过点A(0，－1)和点B(，3)的直线与抛物线C没有公共点，则实数t的取值范围是]‎ A．(－∞，－1)∪(1，＋∞) B．(－∞，－)∪(，＋∞)‎ C．(－∞，－2)∪(2，＋∞) D．(－∞，－)∪(，＋∞)‎ ‎10. 若矩阵满足下列条件：①每行中的四个数所构成的集合均为{1，2，3，4}；②四列中至少有两列的上下两数是相同的．则这样的不同矩阵的个数为 A.48 B‎.72 C.168 D.312‎ 二、填空题：本大题共5小题,每小题5分，共25分.‎ ‎11.已知平面向量a＝(1，2)，b＝(－2，m)，且a∥b，则‎2a＋3b＝________．‎ ‎12．已知D是由不等式组所确定的平面区域，则圆＋＝4在区域D内的弧长为________．‎ ‎13.已知正四面体的俯视图如图所示，其中四边形ABCD是边长为‎2 cm的正方形，则这个四面体的主视图的面积为________cm2.‎ ‎14.直线ax＋by＋c＝0与圆＋＝9相交于两点M、N，若c2＝a2＋b2，则· (O为坐标原点)等于________．‎ ‎15.在锐角△ABC中，角A，B，C的对边分别为a，b，c，若＋＝，则＋的值是________．‎ 三、解答题：本大题共6小题，共75分.‎ ‎16. (本小题满分12分）已知a＝2(，)，b＝(，)(其中0＜＜1)，函数＝a·b，若直线＝是函数图象的一条对称轴．‎ ‎(Ⅰ)试求的值；‎ ‎(Ⅱ)若函数y＝的图象是由y＝的图象的各点的横坐标伸长到原来的2倍，然后再向左平移个单位长度得到，求y＝的单调递增区间．‎ ‎17. (本小题满分12分）有一种密码，明文是由三个字符组成，密码是由明文对应的五个数字组成，编码规则如下表：明文由表中每一排取一个字符组成，且第一排取的字符放在第一位，第二排取的字符放在第二位，第三排取的字符放在第三位，对应的密码由明文对应的数字按相同的次序排成一排组成.‎ 第一排 明文字符 A B C D 密码字符 ‎11‎ ‎12‎ ‎13‎ ‎14‎ 第二排 明文字符 E F G H 密码字符 ‎21‎ ‎22‎ ‎23‎ ‎24‎ 第三排 明文字符 M N P Q 密码字符 ‎1‎ ‎2‎ ‎3‎ ‎4‎ 设随机变量ξ表示密码中不同数字的个数．‎ ‎(Ⅰ)求P(ξ＝2)； (Ⅱ)求随机变量ξ的分布列和它的数学期望．‎ ‎18. (本小题满分12分）等差数列{}的各项均为正数，＝3，前项和为，等比数列{}中，＝1，＝64，{}是公比为64的等比数列．‎ ‎(Ⅰ)求与；] (Ⅱ)证明：＋＋＋…＋<.‎ ‎19. (本小题满分12分）如图，四棱锥P－ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥AD，AB＋AD＝4，CD＝，∠CDA＝45°.‎ ‎(Ⅰ)求证：平面PAB⊥平面PAD；‎ ‎(Ⅱ)设AB＝AP．‎ ‎(ⅰ) 若直线PB与平面PCD所成的角为30°，求线段AB的长；‎ ‎(ⅱ) 在线段AD上是否存在一个点G，使得点G到点P，B，C，D的距离都相等？说明理由．‎ ‎20. (本小题满分13分）给定椭圆C：＋＝1(a>b>0)，称圆心在原点O，半径为的圆是椭圆C的“准圆”．若椭圆C的一个焦点为F(，0)，且其短轴上的一个端点到F的距离为.‎ ‎(Ⅰ)求椭圆C的方程和其“准圆”方程；‎ ‎(Ⅱ)点P是椭圆C的“准圆”上的一个动点，过动点P作直线l1，l2，使得l1，l2与椭圆C都只有一个交点，试判断l1，l2是否垂直，并说明理由．‎ ‎21. (本小题满分14分）‎ 已知函数，为自然对数的底数）.‎ ‎(Ⅰ)当时,求的单调区间；‎ ‎(Ⅱ)若函数在上无零点,求最小值；‎ ‎(Ⅲ)若对任意给定的,在上总存在两个不同的),使成立,求的取值范围.‎ 参考答案 ‎1.【答案】C 【解析】因为A⊆R，所以A中的元素为实数．所以－1＝0.即a＝±1.故应选C.‎ ‎2.【答案】C 【解析】依题意得，该地区高三男生中体重在[56.5，64.5]的学生人数是10000×(0.03＋2×0.05＋0.07)×2＝4000. 故应选C.‎ ‎3.【答案】B 【解析】①中，三条直线两两平行有两种情况：一是一条直线平行于其他两条平行直线构成的平面；二是三条直线共面．②中，三条直线共点最多可确定3个平面，所以当三条直线共点时，三条直线的位置关系有两种情况：一是一条直线与其他两条直线构成的平面相交；二是三条直线共面．③中条件一定能推出三条直线共面．故只有③是空间中三条不同的直线共面的充分条件．故应选B.‎ ‎4.【答案】A 【解析】由于是定义在R上的周期为3的周期函数，所以＋＝f(670×3＋1)＋f(671×3－1)＝f(1)＋f(－1)，而由图像可知f(1)＝1，f(－1)＝2，所以＋＝1＋2＝3. 故应选A.‎ ‎5.【答案】D 【解析】据算法框图可得当k＝9时，S＝11；k＝8时，S＝11＋9＝20.所以应填入k>8. 故应选D.‎ ‎6.【答案】B 【解析】设＝a，＝b，由等比数列的性质知：2(14－a)＝(a－2)2，解得a＝6或a＝－4(舍去)，同理(6－2)(b－14)＝(14－6)2，所以b＝＝30. 故应选B.‎ ‎7.【答案】A 【解析】因为 的展开式中只有第六项的二项式系数最大，所以n＝10，＝··＝，令5－＝0，则r＝2，＝＝180. 故应选A.‎ ‎8.【答案】B 【解析】(特例法)利用等边三角形，过重心作平行于底边BC的直线，易得＝.故应选B.‎ ‎【点评】 本题采用特殊点法，因为过点G的直线有无数条，其中包含平行于底边BC的直线，所以的值不随M、N的位置变化而变化.‎ ‎9.【答案】D 【解析】据已知可得直线AB的方程为＝－1，联立直线与抛物线方程，得，消元整理，得－＋1＝0，由于直线与抛物线无公共点，即方程－＋1＝0无解，故有－8<0，解得>或<－.故应选D.‎ ‎10. 【答案】C 【解析】若恰有两列的上下两数相同，取这两列有种，从1，2，3，4中取2个数排这两列，有种，排另外两列有种，所以共有=144种；若恰有三列的上下两数相同，也是恰有四列上下两数相同，有=24种(只要排其中一行即可). 故一共有144+24=168种. 故应选C.‎ ‎11.【答案】(－4，－8)【解析】由a＝(1，2)，b＝(－2，m)，且a∥b，得1×m＝2×(－2)⇒m＝－4，从而b＝(－2，－4)，那么‎2a＋3b＝2×(1，2)＋3×(－2，－4)＝(－4，－8)．‎ ‎12.【答案】 【解析】作出可行域D及圆＋＝4如图所示，图中阴影部分所在圆心角＝＋所对的弧长即为所求．易知图中两直线的斜率分别是，－得＝，＝，＝＝＝1得＝得弧长＝·＝×2＝ (为圆半径)．‎ ‎13.【答案】2【解析】由俯视图可得，该正四面体AMNC 可视作是如图所示的正方体的一内接几何体，该正方体的棱长为2，正四面体的主视图为三角形，则其面积为×2×＝(cm2)．‎ ‎14.【答案】－7【解析】记、的夹角为.依题意得，圆心(0，0)到直线ax＋by＋c＝0的距离等于＝1，＝，＝－1＝2×－1＝－，·＝3×＝－7.‎ ‎15.【答案】4【解析】方法一　取a＝b＝1，则＝，由余弦定理得c2＝a2＋b2－＝，所以c＝，在如图所示的等腰三角形ABC中，可得＝＝，又＝，＝，所以＋＝4.‎ 方法二　由＋＝6cos C，得＝6·，即a2＋b2＝c2，所以＋＝tan C＝＝＝4.‎ ‎16. 解　(Ⅰ) ＝a·b＝2(，)·(，)‎ ‎＝＋‎ ‎＝1＋cos 2ωx＋sin 2ωx＝1＋2sin. ……………………………2分 因为直线x＝为对称轴，所以sin＝±1，‎ 所以＋＝kπ＋(k∈Z)．所以ω＝k＋(k∈Z)．…………………………4分 因为0＜ω＜1，所以－＜k＜，‎ 所以k＝0，所以ω＝.……………………………………………6分 ‎(Ⅱ)由(Ⅰ)得，得＝1＋2sin，‎ 所以＝1＋2sin＝1＋2sin＝1＋2cos x. ………………8分 由2kπ－π≤x≤2kπ(k∈Z)，得4kπ－2π≤x≤4kπ(k∈Z)，………………………10分 所以的单调递增区间为[4kπ－2π，4kπ](k∈Z)．………………………………12分 ‎17. 解：(Ⅰ)密码中不同数字的个数为2的事件为密码中只有两个数字，注意到密码的第1，2列分别总是1，2，即只能取表格第1，2列中的数字作为密码．‎ 所以P(ξ＝2)＝＝.……………………………………………4分 ‎(Ⅱ)由题意可知，ξ的取值为2，3，4三种情形．‎ 若ξ＝3，注意表格的第一排总含有数字1，第二排总含有数字2则密码中只可能取数字1，2，3或1，2，4.‎ 所以P(ξ＝3)＝＝.……………………………………………6分 P(ξ＝4)＝＝. ……………………………………………8分 所以ξ的分布列为：‎ ξ ‎2‎ ‎3‎ ‎4‎ P ‎…………………………………………………………………………………………8分 所以E(ξ)＝2×＋3×＋4×＝.……………………………………………12分 ‎18. 解：(Ⅰ)设{}的公差为，为正数，{}的公比为，则 ‎＝3＋(－1)，＝. ……………………………………………2分 依题意有，‎ 由知为正有理数，……………………………………4分 又由＝知，d为6的因数1，2，3，6之一，解之得＝2，＝8.‎ 故＝＋1，＝. ……………………………………………6分 ‎(Ⅱ)证明：由(Ⅰ)知Sn＝n(n＋2)，……………………………………7分 ＋＋＋…＋＝＋＋＋…＋ ‎＝ ‎＝<.……………………………………………12分 ‎19. 解：解法一：‎ ‎(Ⅰ)证明：因为PA⊥平面ABCD，AB⊂平面ABCD，‎ 所以PA⊥AB，又AB⊥AD，PA∩AD＝A，‎ 所以AB⊥平面PAD，又AB⊂平面PAB，‎ 所以平面PAB⊥平面PAD，……………………………………………3分 ‎(Ⅱ)以A为坐标原点，建立空间直角坐标系A－xyz(如图)．‎ 在平面ABCD内，作CE∥AB交AD于点E，则CE⊥AD.‎ 在Rt△CDE中，DE＝CD·cos45°＝1，‎ CE＝CD·sin45°＝1.‎ 设AB＝AP＝t, 则B(t，0，0)，P(0，0，t)．‎ 由AB＋AD＝4得AD＝4－t，‎ 所以E(0,3－t,0)，C(1,3－t,0)，D(0,4－t,0)，‎ ‎＝(－1，1,0)，＝(0,4－t，－t)．……………………………………………5分 ‎(ⅰ)设平面PCD的法向量为n＝(x，y，z)．‎ 由n⊥，n⊥，得 取x＝t，得平面PCD的一个法向量n＝(t，t,4－t)．‎ 又＝(t,0，－t)，故由直线PB与平面PCD所成的角为30°得 cos60°＝，即＝.[‎ 解得t＝或t＝4(舍去，因为AD＝4－t>0)，所以AB＝. ………………………7分 ‎(ⅱ)假设在线段AD上存在一个点G，使得点G到点P，B，C，D的距离都相等．‎ 设G(0，m,0)(其中0≤m≤4－t)．‎ 则＝(1,3－t－m,0)，＝(0,4－t－m,0)，‎ ‎＝(0，－m，t)．‎ 由||＝||，得12＋(3－t－m)2＝(4－t－m)2，‎ 即t＝3－m； ①‎ 由||＝||，得(4－t－m)2＝m2＋t2. ②‎ 由①、②消去t，化简得m2－‎3m＋4＝0. ③‎ 由于方程③没有实数根，所以在线段AD上不存在一个点G，使得点G到点P，C，D的距离都相等．‎ 从而，在线段AD上不存在一个点G，‎ 使得点G到点P，B，C，D的距离都相等．……………………………………12分 解法二：‎ ‎(Ⅰ)同解法一：‎ ‎(Ⅱ)(ⅰ)以A为坐标原点，建立空间直角坐标系A－xyz(如图)．‎ 在平面ABCD内，作CE∥AB交AD于点E，‎ 则CE⊥AD，‎ 在Rt△CDE中，‎ DE＝CDcos45°＝1，‎ CE＝CD·sin45°＝1.‎ 设AB＝AP＝t，则B(t,0,0)，P(0,0，t)．‎ 由AB＋AD＝4得AD＝4－t.‎ 所以E(0,3－t,0)，C(t,3－t,0)，D(0,4－t,0)．‎ ‎＝(－1,1,0)，＝(0,4－t，－t)．‎ 设平面PCD的法向量为n＝(x，y，z)[‎ 由n⊥，n⊥，得 取x＝t，得平面PCD的一个法向量n＝(t，t,4－t)，‎ 又＝(t,0，－t)，故由直线PB与平面PCD所成的角为30°得cos60°＝，‎ 即＝，解得t＝或t＝4(舍去，因为AD＝4－t>0)，‎ 所以AB＝.‎ ‎(ⅱ)假设在线段AD上存在一个点G，使得点G到点P，B，C，D的距离都相等．‎ 由GC＝GD，得∠GCD＝∠GDC＝45°，‎ 从而∠CGD＝90°，即CG⊥AD，‎ 所以GD＝CD·cos45°＝1.‎ 设AB＝λ，则AD＝4－λ，AG＝AD－GD＝3－λ.‎ 在Rt△ABG中，‎ GB＝＝＝ >1，这与GB＝GD矛盾．‎ 所以在线段AD上不存在一个点G，使得点G到B，C，D的距离都相等．‎ 从而，在线段AD上不存在一个点G，使得点G到点P，B，C，D的距离都相等．‎ ‎20. 解：(Ⅰ)由题意可知c＝，b2＋c2＝()2，则a＝，b＝1，‎ 所以椭圆方程为＋y2＝1. ………………………………………………2分 易知准圆半径为＝2，‎ 则准圆方程为x2＋y2＝4. ………………………………………………………4分 ‎(Ⅱ)①当l1，l2中有一条直线的斜率不存在时，‎ 不妨设l1的斜率不存在，因为l1与椭圆只有一个公共点，则其方程为x＝±，‎ 当l1的方程为x＝时，此时l1与准圆交于点(，1)，(，－1)，‎ 此时经过点(，1)或(，－1)且与椭圆只有一个公共点的直线是y＝1或y＝－1，‎ 即l2为y＝1或y＝－1，显然直线l1，l2垂直；……………………………6分 同理可证直线l1的方程为x＝－时，直线l1，l2也垂直．………………7分 ‎②当l1，l2的斜率都存在时，设点P(x0，y0)，其中x＋y＝4.‎ 设经过点P(x0，y0)与椭圆只有一个公共点的直线为y＝t(x－x0)＋y0，‎ 由消去y，得(1＋3t2)x2＋6t(y0－tx0)x＋3(y0－tx0)2－3＝0.‎ 由Δ＝0化简整理得，(3－x)t2＋2x0y0t＋1－y＝0. 因为x＋y＝4，‎ 所以有(3－x)t2＋2x0y0t＋x－3＝0. …………………………………………10分 设直线l1，l2的斜率分别为t1，t2，因为l1，l2与椭圆只有一个公共点，‎ 所以t1，t2满足方程(3－x)t2＋2x0y0t＋x－3＝0，‎ 所以t1·t2＝－1，即l1，l2垂直．………………………………………………12分 综合①②知，l1，l2垂直． ………………………………………………13分 ‎21.解：(Ⅰ)当时, ()，则. ……1分 由得；由得. ………………3分 故的单调递减区间为(0，2)，单调递增区间为(2，). ………………4分 ‎(Ⅱ)因为在区间上恒成立是不可能的, ………………5分 故要使函数在上无零点,只要对任意,恒成立.‎ 即对，恒成立. ………………6分 令，，则，‎ 再令，，则.‎ 故在为减函数，于是，‎ 从而，于是在上为增函数，‎ 所以，………………………………8分 故要使恒成立，只要.‎ 综上可知，若函数在上无零点，则的最小值为.………9分 ‎(Ⅲ)，所以在上递增，在上递减.‎ 又，，‎ 所以函数在上的值域为.………………………………10分 当时，不合题意；‎ 当时，， .‎ 当时，，由题意知，在上不单调，‎ 故，即………………………………11分 此时，当变化时，，的变化情况如下：‎ ‎—‎ ‎0‎ ‎+‎ ‎↘‎ 最小值 ‎↗‎ 又因为当时，，‎ ‎，，‎ 所以，对任意给定的，在上总存在两个不同的），‎ 使得成立，当且仅当满足下列条件：‎ ‎， ………………12分 令，，则，‎ 故当时，函数单调递增，‎ 当时，函数单调递减，‎ 所以，对任意的，有，‎ 即(2)对任意恒成立，则(3)式解得 (4) . …………13分 综合(1)与(4)可知，当时，对任意给定的，‎ 在上总存在两个不同的），使得成立.………………14分