四川省广元市川师大万达中学2019-2020高一上学期教学质量检测数学试卷

四川省广元市川师大万达中学2019-2020高一上学期教学质量检测数学试卷

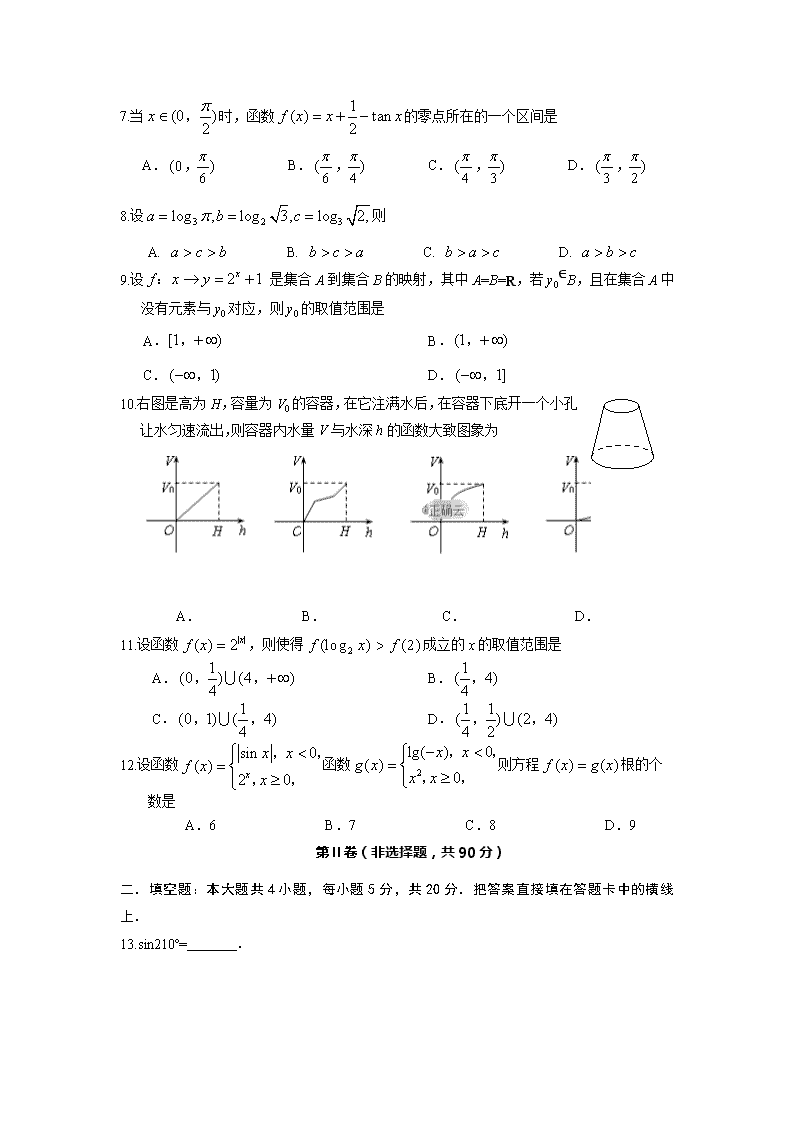
数学试卷 注意事项：‎ ‎1．答题前，考生务必将自己的学校、班级、姓名用0.5毫米黑色签字笔填写清楚，同时用2B铅笔将考号准确填涂在“考号”栏目内．‎ ‎2．选择题使用2B铅笔填涂在答题卡对应题目标号的位置上，如需改动，用橡皮擦擦干净后再选涂其它答案；非选择题用0.5毫米黑色签字笔书写在答题卡的对应框内，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．‎ ‎3．考试结束后将答题卡收回． ‎ 第Ⅰ卷（选择题，共60分）‎ 一． 选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个是符合题目要求的．‎ ‎1.设集合，则 A. B. C. D. ‎ ‎2.角α的终边在直线2x+y=0上，则tanα=‎ A． B． C． D．‎ ‎3.幂函数的图象经过点，则是 A. 偶函数，且在上是增函数 B. 偶函数，且在上是减函数 C. 奇函数，且在上是减函数 D. 非奇非偶函数，且在上是增函数 ‎4.已知扇形的周长为10cm，则当扇形面积最大时，扇形的圆心角等于 A. 1 B. 2 C. D. ‎ ‎5.已知sin(35º+α)=，则cos(55º-α)的值为 ‎ A． B． C． D． ‎ ‎6.函数(x∈R)图象的一个对称中心可以是 A．（0，0） B．（，1） C．（，0） D．（，0）‎ ‎7.当时，函数的零点所在的一个区间是 A． B． C． D．‎ ‎8.设则 A. B. C. D. ‎ ‎9.设 是集合A到集合B的映射，其中A=B=R，若y0∈B，且在集合A中没有元素与y0对应，则y0的取值范围是 A． B．‎ C． D． ‎ ‎10.右图是高为H，容量为V0的容器，在它注满水后，在容器下底开一个小孔让水匀速流出，则容器内水量V与水深h的函数大致图象为 A． B． C． D．‎ ‎11.设函数，则使得成立的x的取值范围是 A． B．‎ C． D．‎ ‎12.设函数函数则方程根的个数是 A．6 B．7 C．8 D．9 ‎ 第Ⅱ卷（非选择题，共90分）‎ 二．填空题：本大题共4小题，每小题5分，共20分．把答案直接填在答题卡中的横线上．‎ ‎13.sin210º= ．‎ ‎14.已知函数 则f(f())=______．‎ ‎15.若函数f(x)=loga(1-2ax)(a>0，且a≠1)在[1，4]上有最大值1，则a=______．‎ ‎16.若函数是R上的奇函数，且对任意的x∈R有，当∈时，，则()= ．‎ 三．解答题：本大题共6小题，第17题至21题每题12分,22题10分．解答应写出文字说明、证明过程或演算步骤 ‎17.(本小题满分12分)设集合U=R，；‎ ‎（1）求：，；‎ ‎（2）设集合，若，求a的取值范围．‎ ‎18.(本小题满分12分)已知 ‎ （1）化简；‎ ‎（2）若，且，求的值；‎ ‎（3）若，求的值． ‎ ‎19.(本小题满分12分)如图，在△OAB中，顶点A的坐标是(3，0)，顶点B的坐标是(1，2)， 记△OAB位于直线左侧图形的面积为f(t)．‎ ‎（1）求函数f(t)的解析式；‎ ‎（2）设函数，求函数的最大值．‎ ‎20.(本小题满分12分)函数()的部分图象如图所示．‎ ‎（1）求函数的解析式；‎ ‎（2）求函数的单调递减区间；‎ ‎（3）已知当时，求函数的最大值， 并求出此时x的值．‎ ‎21.(本小题满分12分)已知函数，x∈R．‎ ‎（1）判断函数的奇偶性，并说明理由； ‎ ‎（2）利用函数单调性定义证明：在上是增函数； ‎ ‎（3）若f(x)≥（m>0，k∈R）对任意的x∈R，任意的m∈ 恒成立，求实数k的取值范围．‎ ‎22.(本小题满分10分)计算下列各式的值.‎ ‎（1） ‎ ‎（2） ‎ 参考答案及评分意见 一、选择题：本大题共12小题，每小题5分，共60分．‎ ‎1~5 DBDBA 6~10 DCDDC 11~12 AB ‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13． 14． 15． 16． ‎ 三、解答题：本大题共6小题．解答应写出必要的文字说明、证明过程或演算步骤．‎ ‎17．（满分12分）解：（1）……………………………3分 ‎，，………………6分 ‎（2），i) 时，，………………8分 ii) 时，………………11分 综上：．………………12分 ‎18.(满分12分)解：（1）………………………4分 ‎（2）………………………8分 ‎（3）………………………12分 ‎19．（满分12分）解：（1）∵ A的坐标是(3，0)，B的坐标是(1，2)，‎ ‎ 易得直线OB的解析式为y=2x，直线AB的解析式为y=3-x．‎ 当0

查看更多