2013年山东省高考数学试卷（理科）

2013年山东省高考数学试卷（理科）

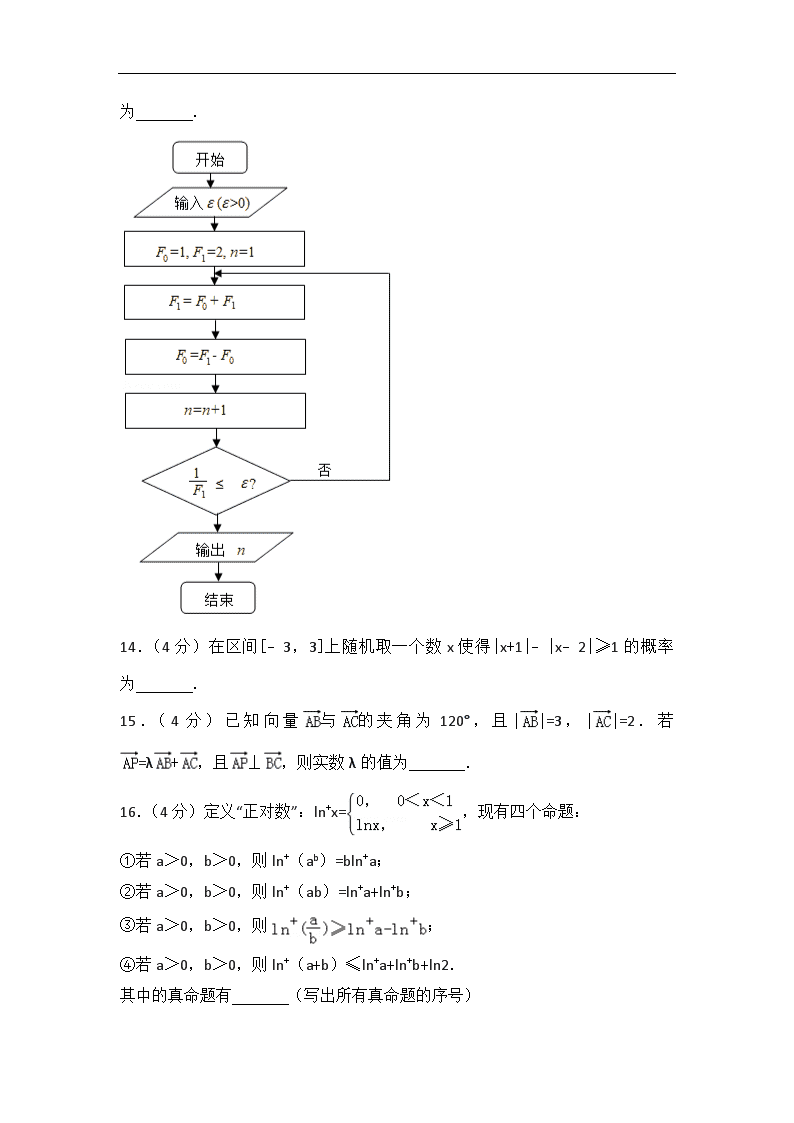
‎2013年山东省高考数学试卷（理科）‎ ‎　‎ 一、选择题 ‎1．（5分）复数z满足（z﹣3）（2﹣i）=5（i为虚数单位），则z的共轭复数为（　　）‎ A．2+i B．2﹣i C．5+i D．5﹣i ‎2．（5分）已知集合A={0，1，2}，则集合B={x﹣y|x∈A，y∈A}中元素的个数是（　　）‎ A．1 B．3 C．5 D．9‎ ‎3．（5分）已知函数f（x）为奇函数，且当x＞0时，，则f（﹣1）=（　　）‎ A．﹣2 B．0 C．1 D．2‎ ‎4．（5分）已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直，体积为，底面是边长为的正三角形，若P为底面A1B1C1的中心，则PA与平面A1B1C1所成角的大小为（　　）‎ A． B． C． D．‎ ‎5．（5分）函数y=sin（2x+φ）的图象沿x轴向左平移个单位后，得到一个偶函数的图象，则φ的一个可能的值为（　　）‎ A． B． C．0 D．‎ ‎6．（5分）在平面直角坐标系xOy中，M为不等式组所表示的区域上一动点，则直线OM斜率的最小值为（　　）‎ A．2 B．1 C． D．‎ ‎7．（5分）给定两个命题p，q．若￢p是q的必要而不充分条件，则p是￢q的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎8．（5分）函数y=xcosx+sinx的图象大致为（　　）‎ A． B． C． D．‎ ‎9．（5分）过点（3，1）作圆（x﹣1）2+y2=1的两条切线，切点分别为A，B，则直线AB的方程为（　　）‎ A．2x+y﹣3=0 B．2x﹣y﹣3=0 C．4x﹣y﹣3=0 D．4x+y﹣3=0‎ ‎10．（5分）用0，1，2，…，9十个数字，可以组成有重复数字的三位数的个数为（　　）‎ A．243 B．252 C．261 D．279‎ ‎11．（5分）抛物线C1：的焦点与双曲线C2：的右焦点的连线交C1于第一象限的点M．若C1在点M处的切线平行于C2的一条渐近线，则p=（　　）‎ A． B． C． D．‎ ‎12．（5分）设正实数x，y，z满足x2﹣3xy+4y2﹣z=0．则当取得最大值时，的最大值为（　　）‎ A．0 B．1 C． D．3‎ ‎　‎ 二、填空题 ‎13．（4分）执行右面的程序框图，若输入的ɛ值为0.25，则输出的n值为　 　．‎ ‎14．（4分）在区间[﹣3，3]上随机取一个数x使得|x+1|﹣|x﹣2|≥1的概率为　 　．‎ ‎15．（4分）已知向量与的夹角为120°，且||=3，||=2．若=λ+，且⊥，则实数λ的值为　 　．‎ ‎16．（4分）定义“正对数”：ln+x=，现有四个命题：‎ ‎①若a＞0，b＞0，则ln+（ab）=bln+a；‎ ‎②若a＞0，b＞0，则ln+（ab）=ln+a+ln+b；‎ ‎③若a＞0，b＞0，则；‎ ‎④若a＞0，b＞0，则ln+（a+b）≤ln+a+ln+b+ln2．‎ 其中的真命题有　 　（写出所有真命题的序号）‎ ‎　‎ 三、解答题 ‎17．（12分）设△ABC的内角A，B，C所对边分别为a，b，c，且a+c=6，b=2，cosB=．‎ ‎（1）求a，c的值；‎ ‎（2）求sin（A﹣B）的值．‎ ‎18．（12分）如图所示，在三棱锥P﹣ABQ中，PB⊥平面ABQ，BA=BP=BQ，D，C，E，F分别是AQ，BQ，AP，BP的中点，AQ=2BD，PD与EQ交于点G，PC与FQ交于点H，连接GH．‎ ‎（1）求证：AB∥GH；‎ ‎（2）求二面角D﹣GH﹣E的余弦值．‎ ‎19．（12分）甲乙两支排球队进行比赛，先胜3局者获得比赛的胜利，比赛随即结束．除第五局甲队获胜的概率是，其余每局比赛甲队获胜的概率都是．设各局比赛结果相互独立．‎ ‎（1）分别求甲队3：0，3：1，3：2胜利的概率；‎ ‎（2）若比赛结果3：0或3：1，则胜利方得3分，对方得0分；若比赛结果为3：2，则胜利方得2分，对方得1分，求乙队得分X的分布列及数学期望．‎ ‎20．（12分）设等差数列{an}的前n项和为Sn，且S4=4S2，a2n=2an+1．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）设数列{bn}的前n项和为Tn且（λ为常数）．令cn=b2n（n∈‎ N*）求数列{cn}的前n项和Rn．‎ ‎21．（13分）设函数．‎ ‎（1）求f（x）的单调区间及最大值；‎ ‎（2）讨论关于x的方程|lnx|=f（x）根的个数．‎ ‎22．（13分）椭圆C：的左右焦点分别是F1，F2，离心率为，过F1且垂直于x轴的直线被椭圆C截得的线段长为1．‎ ‎（1）求椭圆C的方程；‎ ‎（2）点P是椭圆C上除长轴端点外的任一点，连接PF1，PF2，设∠F1PF2的角平分线PM交C的长轴于点M（m，0），求m的取值范围；‎ ‎（3）在（2）的条件下，过点P作斜率为k的直线l，使得l与椭圆C有且只有一个公共点，设直线PF1，PF2的斜率分别为k1，k2，若k≠0，试证明为定值，并求出这个定值．‎ ‎　‎ ‎2013年山东省高考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题 ‎1．（5分）复数z满足（z﹣3）（2﹣i）=5（i为虚数单位），则z的共轭复数为（　　）‎ A．2+i B．2﹣i C．5+i D．5﹣i ‎【分析】利用复数的运算法则求得z，即可求得z的共轭复数．‎ ‎【解答】解：∵（z﹣3）（2﹣i）=5，‎ ‎∴z﹣3==2+i ‎∴z=5+i，‎ ‎∴=5﹣i．‎ 故选：D．‎ ‎【点评】本题考查复数的基本概念与基本运算，求得复数z是关键，属于基础题．‎ ‎　‎ ‎2．（5分）已知集合A={0，1，2}，则集合B={x﹣y|x∈A，y∈A}中元素的个数是（　　）‎ A．1 B．3 C．5 D．9‎ ‎【分析】依题意，可求得集合B={﹣2，﹣1，0，1，2}，从而可得答案．‎ ‎【解答】解：∵A={0，1，2}，B={x﹣y|x∈A，y∈A}，‎ ‎∴当x=0，y分别取0，1，2时，x﹣y的值分别为0，﹣1，﹣2；‎ 当x=1，y分别取0，1，2时，x﹣y的值分别为1，0，﹣1；‎ 当x=2，y分别取0，1，2时，x﹣y的值分别为2，1，0；‎ ‎∴B={﹣2，﹣1，0，1，2}，‎ ‎∴集合B={x﹣y|x∈A，y∈A}中元素的个数是5个．‎ 故选：C．‎ ‎【点评】本题考查集合中元素个数的最值，理解题意是关键，考查分析运算能力，属于中档题．‎ ‎　‎ ‎3．（5分）已知函数f（x）为奇函数，且当x＞0时，，则f（﹣1）=（　　）‎ A．﹣2 B．0 C．1 D．2‎ ‎【分析】利用奇函数的性质，f（﹣1）=﹣f（1），即可求得答案．‎ ‎【解答】解：∵函数f（x）为奇函数，x＞0时，f（x）=x2+，‎ ‎∴f（﹣1）=﹣f（1）=﹣2，‎ 故选：A．‎ ‎【点评】本题考查奇函数的性质，考查函数的求值，属于基础题．‎ ‎　‎ ‎4．（5分）已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直，体积为，底面是边长为的正三角形，若P为底面A1B1C1的中心，则PA与平面A1B1C1所成角的大小为（　　）‎ A． B． C． D．‎ ‎【分析】利用三棱柱ABC﹣A1B1C1的侧棱与底面垂直和线面角的定义可知，∠APA1为PA与平面A1B1C1所成角，即为∠APA1为PA与平面ABC所成角．利用三棱锥的体积计算公式可得AA1，再利用正三角形的性质可得A1P，在Rt△AA1P中，利用tan∠APA1=即可得出．‎ ‎【解答】解：如图所示，‎ ‎∵AA1⊥底面A1B1C1，∴∠APA1为PA与平面A1B1C1所成角，‎ ‎∵平面ABC∥平面A1B1C1，∴∠APA1为PA与平面ABC所成角．‎ ‎∵==．‎ ‎∴V三棱柱ABC﹣A1B1C1==，解得．‎ 又P为底面正三角形A1B1C1的中心，∴==1，‎ 在Rt△AA1P中，，‎ ‎∴．‎ 故选：B．‎ ‎【点评】熟练掌握三棱柱的性质、体积计算公式、正三角形的性质、线面角的定义是解题的关键．‎ ‎　‎ ‎5．（5分）函数y=sin（2x+φ）的图象沿x轴向左平移个单位后，得到一个偶函数的图象，则φ的一个可能的值为（　　）‎ A． B． C．0 D．‎ ‎【分析】利用函数y=Asin（ωx+φ）的图象变换可得函数y=sin（2x+φ）的图象沿x轴向左平移个单位后的解析式，利用其为偶函数即可求得答案．‎ ‎【解答】解：令y=f（x）=sin（2x+φ），‎ 则f（x+）=sin[2（x+）+φ]=sin（2x++φ），‎ ‎∵f（x+）为偶函数，‎ ‎∴+φ=kπ+，‎ ‎∴φ=kπ+，k∈Z，‎ ‎∴当k=0时，φ=．‎ 故φ的一个可能的值为．‎ 故选：B．‎ ‎【点评】本题考查函数y=Asin（ωx+φ）的图象变换，考查三角函数的奇偶性，属于中档题．‎ ‎　‎ ‎6．（5分）在平面直角坐标系xOy中，M为不等式组所表示的区域上一动点，则直线OM斜率的最小值为（　　）‎ A．2 B．1 C． D．‎ ‎【分析】本题属于线性规划中的延伸题，对于可行域不要求线性目标函数的最值，而是求可行域内的点与原点（0，0）构成的直线的斜率的最小值即可．‎ ‎【解答】解：不等式组表示的区域如图，‎ 当M取得点A（3，﹣1）时，‎ z直线OM斜率取得最小，最小值为 k==﹣．‎ 故选：C．‎ ‎【点评】本题利用直线斜率的几何意义，求可行域中的点与原点的斜率．本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．‎ ‎　‎ ‎7．（5分）给定两个命题p，q．若￢p是q的必要而不充分条件，则p是￢q的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【分析】根据互为逆否命题真假性相同，可将已知转化为q是¬p的充分不必要条件，进而根据逆否命题及充要条件的定义得到答案．‎ ‎【解答】解：∵¬p是q的必要而不充分条件，‎ ‎∴q是¬p的充分不必要条件，即q⇒¬p，但¬p不能⇒q，‎ 其逆否命题为p⇒¬q，但¬q不能⇒p，‎ 则p是¬q的充分不必要条件．‎ 故选：A．‎ ‎【点评】本题考查的知识点是充要条件的判断，其中将已知利用互为逆否命题真假性相同，转化为q是¬p的充分不必要条件，是解答的关键．‎ ‎　‎ ‎8．（5分）函数y=xcosx+sinx的图象大致为（　　）‎ A． B． C． D．‎ ‎【分析】给出的函数是奇函数，奇函数图象关于原点中心对称，由此排除B，然后利用区特值排除A和C，则答案可求．‎ ‎【解答】解：因为函数y=xcosx+sinx为奇函数，所以排除选项B，‎ 由当x=时，，‎ 当x=π时，y=π×cosπ+sinπ=﹣π＜0．‎ 由此可排除选项A和选项C．‎ 故正确的选项为D．‎ 故选：D．‎ ‎【点评】本题考查了函数的图象，考查了函数的性质，考查了函数的值，是基础题．‎ ‎　‎ ‎9．（5分）过点（3，1）作圆（x﹣1）2+y2=1的两条切线，切点分别为A，B，则直线AB的方程为（　　）‎ A．2x+y﹣3=0 B．2x﹣y﹣3=0 C．4x﹣y﹣3=0 D．4x+y﹣3=0‎ ‎【分析】由题意判断出切点（1，1）代入选项排除B、D，推出令一个切点判断切线斜率，得到选项即可．‎ ‎【解答】解：因为过点（3，1）作圆（x﹣1）2+y2‎ ‎=1的两条切线，切点分别为A，B，所以圆的一条切线方程为y=1，切点之一为（1，1），显然B、D选项不过（1，1），B、D不满足题意；另一个切点的坐标在（1，﹣1）的右侧，所以切线的斜率为负，选项C不满足，A满足．‎ 故选：A．‎ ‎【点评】本题考查直线与圆的位置关系，圆的切线方程求法，可以直接解答，本题的解答是间接法，值得同学学习．‎ ‎　‎ ‎10．（5分）用0，1，2，…，9十个数字，可以组成有重复数字的三位数的个数为（　　）‎ A．243 B．252 C．261 D．279‎ ‎【分析】求出所有三位数的个数，减去没有重复数字的三位数个数即可．‎ ‎【解答】解：用0，1，2，…，9十个数字，所有三位数个数为：900，‎ 其中没有重复数字的三位数百位数从非0的9个数字中选取一位，十位数从余下的9个数字中选一个，个位数再从余下的8个中选一个，所以共有：9×9×8=648，‎ 所以可以组成有重复数字的三位数的个数为：900﹣648=252．‎ 故选：B．‎ ‎【点评】本题考查排列组合以及简单计数原理的应用，利用间接法求解是解题的关键，考查计算能力．‎ ‎　‎ ‎11．（5分）抛物线C1：的焦点与双曲线C2：的右焦点的连线交C1于第一象限的点M．若C1在点M处的切线平行于C2的一条渐近线，则p=（　　）‎ A． B． C． D．‎ ‎【分析】由曲线方程求出抛物线与双曲线的焦点坐标，由两点式写出过两个焦点的直线方程，求出函数在x取直线与抛物线交点M的横坐标时的导数值，由其等于双曲线渐近线的斜率得到交点横坐标与p的关系，把M点的坐标代入直线方程即可求得p的值．‎ ‎【解答】解：由，得x2=2py（p＞0），‎ 所以抛物线的焦点坐标为F（）．‎ 由，得，．‎ 所以双曲线的右焦点为（2，0）．‎ 则抛物线的焦点与双曲线的右焦点的连线所在直线方程为，‎ 即①．‎ 设该直线交抛物线于M（），则C1在点M处的切线的斜率为．‎ 由题意可知，得，代入M点得M（）‎ 把M点代入①得：．‎ 解得p=．‎ 故选：D．‎ ‎【点评】本题考查了双曲线的简单几何性质，考查了利用导数研究曲线上某点的切线方程，函数在曲线上某点处的切线的斜率等于函数在该点处的导数，是中档题．‎ ‎　‎ ‎12．（5分）设正实数x，y，z满足x2﹣3xy+4y2﹣z=0．则当取得最大值时，的最大值为（　　）‎ A．0 B．1 C． D．3‎ ‎【分析】依题意，当取得最大值时x=2y，代入所求关系式f（y）=+﹣，利用配方法即可求得其最大值．‎ ‎【解答】解：∵x2﹣3xy+4y2﹣z=0，‎ ‎∴z=x2﹣3xy+4y2，又x，y，z均为正实数，‎ ‎∴==≤=1（当且仅当x=2y时取“=”），‎ ‎∴=1，此时，x=2y．‎ ‎∴z=x2﹣3xy+4y2=（2y）2﹣3×2y×y+4y2=2y2，‎ ‎∴+﹣=+﹣=﹣+1≤1，当且仅当y=1时取得“=”，满足题意．‎ ‎∴的最大值为1．‎ 故选：B．‎ ‎【点评】本题考查基本不等式，由取得最大值时得到x=2y是关键，考查配方法求最值，属于中档题．‎ ‎　‎ 二、填空题 ‎13．（4分）执行右面的程序框图，若输入的ɛ值为0.25，则输出的n值为　3　．‎ ‎【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算并输出n的值．‎ ‎【解答】解：循环前，F0=1，F1=2，n=1，‎ 第一次循环，F0=1，F1=3，n=2，‎ 第二次循环，F0=2，F1=4，n=3，‎ 此时，满足条件，退出循环，输出n=3，‎ 故答案为：3．‎ ‎【点评】本题主要考查了直到循环结构，根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，属于基础题．‎ ‎　‎ ‎14．（4分）在区间[﹣3，3]上随机取一个数x使得|x+1|﹣|x﹣2|≥1的概率为　　．‎ ‎【分析】本题利用几何概型求概率．先解绝对值不等式，再利用解得的区间长度与区间[﹣3，3]的长度求比值即得．‎ ‎【解答】解：利用几何概型，其测度为线段的长度．‎ 由不等式|x+1|﹣|x﹣2|≥1 可得 ①，或②，‎ ‎③．‎ 解①可得x∈∅，解②可得1≤x＜2，解③可得 x≥2．‎ 故原不等式的解集为{x|x≥1}，‎ ‎∴|在区间[﹣3，3]上随机取一个数x使得|x+1|﹣|x﹣2|≥1的概率为P==．‎ 故答案为：‎ ‎【点评】本题主要考查了几何概型，简单地说，如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．‎ ‎　‎ ‎15．（4分）已知向量与的夹角为120°，且||=3，||=2．若=λ+，且⊥，则实数λ的值为　　．‎ ‎【分析】利用，，表示向量，通过数量积为0，求出λ的值即可．‎ ‎【解答】解：由题意可知：，‎ 因为，‎ 所以，‎ 所以 ‎=‎ ‎=‎ ‎=﹣12λ+7=0‎ 解得λ=．‎ 故答案为：．‎ ‎【点评】本题考查向量的数量积的应用，向量的垂直，考查转化数学与计算能力．‎ ‎　‎ ‎16．（4分）定义“正对数”：ln+x=，现有四个命题：‎ ‎①若a＞0，b＞0，则ln+（ab）=bln+a；‎ ‎②若a＞0，b＞0，则ln+（ab）=ln+a+ln+b；‎ ‎③若a＞0，b＞0，则；‎ ‎④若a＞0，b＞0，则ln+（a+b）≤ln+a+ln+b+ln2．‎ 其中的真命题有　①③④　（写出所有真命题的序号）‎ ‎【分析】由题意，根据所给的定义及对数的运算性质对四个命题进行判断，由于在不同的定义域中函数的解析式不一样，故需要对a，b分类讨论，判断出每个命题的真假．‎ ‎【解答】解：（1）对于①，由定义，当a≥1时，ab≥1，故ln+（ab）=ln（ab）=blna，又bln+a=blna，故有ln+（ab）=bln+a；当a＜1时，ab＜1，故ln+（ab）=0，又a＜1时bln+a=0，所以此时亦有ln+（ab）=bln+a，故①正确；‎ ‎（2）对于②，此命题不成立，可令a=2，b=，则ab=，由定义ln+（ab）=0，ln+a+ln+b=ln2，所以ln+（ab）≠ln+a+ln+b，故②错误；‎ ‎（3）对于③，‎ i．≥1时，此时≥0，‎ 当a≥b≥1时，ln+a﹣ln+b=lna﹣lnb=，此时则，命题成立；‎ 当a＞1＞b＞0时，ln+a﹣ln+b=lna，此时，＞lna，则 ‎，命题成立；‎ 当1＞a≥b＞0时，ln+a﹣ln+b=0，成立；‎ ii．＜1时，同理可验证是正确的，故③正确；‎ ‎（4）对于④，‎ 当a≥1，b≥1时，ln+（a+b）=ln（a+b），ln+a+ln+b+ln2=lna+lnb+ln2=ln（2ab），‎ ‎∵a+b﹣2ab=a﹣ab+b﹣ab=a（1﹣b）+b（1﹣a）≤0，‎ ‎∴a+b≤2ab，‎ ‎∴ln（a+b）＜ln（2ab），‎ ‎∴ln+（a+b）≤ln+a+ln+b+ln2．‎ 当a＞1，0＜b＜1时，ln+（a+b）=ln（a+b），ln+a+ln+b+ln2=lna+ln2=ln（2a），‎ ‎∵a+b﹣2a=b﹣a≤0，‎ ‎∴a+b≤2a，‎ ‎∴ln（a+b）＜ln（2a），‎ ‎∴ln+（a+b）≤ln+a+ln+b+ln2．‎ 当b＞1，0＜a＜1时，同理可证ln+（a+b）≤ln+a+ln+b+ln2．‎ 当0＜a＜1，0＜b＜1时，可分a+b≥1和a+b＜1两种情况，均有ln+（a+b）≤ln+a+ln+b+ln2．‎ 故④正确．‎ 故答案为①③④．‎ ‎【点评】本题考查新定义及对数的运算性质，理解定义所给的运算规则是解题的关键，本题考查了分类讨论的思想，逻辑判断的能力，综合性较强，探究性强．易因为理解不清定义及忘记分类讨论的方法解题导致无法入手致错．‎ ‎　‎ 三、解答题 ‎17．（12分）设△ABC的内角A，B，C所对边分别为a，b，c，且a+c=6，b=2，cosB=．‎ ‎（1）求a，c的值；‎ ‎（2）求sin（A﹣B）的值．‎ ‎【分析】（1）利用余弦定理列出关系式，将b与cosB的值代入，利用完全平方公式变形，求出acb的值，与a+c的值联立即可求出a与c的值即可；‎ ‎（2）先由cosB的值，利用同角三角函数间的基本关系求出sinB的值，再由a，b及sinB的值，利用正弦定理求出sinA的值，进而求出cosA的值，所求式子利用两角和与差的正弦函数公式化简后，将各自的值代入计算即可求出值．‎ ‎【解答】解：（1）∵a+c=6①，b=2，cosB=，‎ ‎∴由余弦定理得：b2=a2+c2﹣2accosB=（a+c）2﹣2ac﹣ac=36﹣ac=4，‎ 整理得：ac=9②，‎ 联立①②解得：a=c=3；‎ ‎（2）∵cosB=，B为三角形的内角，‎ ‎∴sinB==，‎ ‎∵b=2，a=3，sinB=，‎ ‎∴由正弦定理得：sinA===，‎ ‎∵a=c，即A=C，∴A为锐角，‎ ‎∴cosA==，‎ 则sin（A﹣B）=sinAcosB﹣cosAsinB=×﹣×=．‎ ‎【点评】此题考查了正弦、余弦定理，两角和与差的正弦函数公式，以及同角三角函数间的基本关系，熟练掌握定理及公式是解本题的关键．‎ ‎　‎ ‎18．（12分）如图所示，在三棱锥P﹣ABQ中，PB⊥平面ABQ，BA=BP=BQ，D，C，E，F分别是AQ，BQ，AP，BP的中点，AQ=2BD，PD与EQ交于点G，PC与FQ交于点H，连接GH．‎ ‎（1）求证：AB∥GH；‎ ‎（2）求二面角D﹣GH﹣E的余弦值．‎ ‎【分析】（1）由给出的D，C，E，F分别是AQ，BQ，AP，BP的中点，利用三角形中位线知识及平行公理得到DC平行于EF，再利用线面平行的判定和性质得到DC平行于GH，从而得到AB∥GH；‎ ‎（2）由题意可知BA、BQ、BP两两相互垂直，以B为坐标原点建立空间直角坐标系，设出BA、BQ、BP的长度，标出点的坐标，求出一些向量的坐标，利用二面角的两个面的法向量所成的角的余弦值求解二面角D﹣GH﹣E的余弦值．‎ ‎【解答】（1）证明：如图，‎ ‎∵C，D为AQ，BQ的中点，∴CD∥AB，‎ 又E，F分别AP，BP的中点，∴EF∥AB，‎ 则EF∥CD．又EF⊂平面EFQ，∴CD∥平面EFQ．‎ 又CD⊂平面PCD，且平面PCD∩平面EFQ=GH，∴CD∥GH．‎ 又AB∥CD，∴AB∥GH；‎ ‎（2）由AQ=2BD，D为AQ的中点可得，三角形ABQ为直角三角形，‎ 以B为坐标原点，分别以BA、BQ、BP所在直线为x、y、z轴建立空间直角坐标系，‎ 设AB=BP=BQ=2，‎ 则D（1，1，0），C（0，1，0），E（1，0，1），F（0，0，1），‎ 因为H为三角形PBQ的重心，所以H（0，，）．‎ 则，‎ ‎，．‎ 设平面GCD的一个法向量为 由，得，取z1=1，得y1=2．‎ 所以．‎ 设平面EFG的一个法向量为 由，得，取z2=2，得y2=1．‎ 所以．‎ 所以=．‎ 则二面角D﹣GH﹣E的余弦值等于．‎ ‎【点评】本题考查了直线与平面平行的性质，考查了二面角的平面角及其求法，考查了学生的空间想象能力和思维能力，考查了计算能力，解答此题的关键是正确求出H点的坐标，是中档题．‎ ‎　‎ ‎19．（12分）甲乙两支排球队进行比赛，先胜3局者获得比赛的胜利，比赛随即结束．除第五局甲队获胜的概率是，其余每局比赛甲队获胜的概率都是．设各局比赛结果相互独立．‎ ‎（1）分别求甲队3：0，3：1，3：2胜利的概率；‎ ‎（2）若比赛结果3：0或3：1，则胜利方得3分，对方得0分；若比赛结果为3：2，则胜利方得2分，对方得1分，求乙队得分X的分布列及数学期望．‎ ‎【分析】（1）甲队获胜有三种情形，①3：0，②3：1，③3：2，其每种情形的最后一局肯定是甲队胜，分别求出相应的概率，最后根据互斥事件的概率公式求出甲队获得这次比赛胜利的概率；‎ ‎（2）X的取值可能为0，1，2，3，然后利用相互独立事件的概率乘法公式求出相应的概率，列出分布列，最后根据数学期望公式解之即可．‎ ‎【解答】解：（1）甲队获胜有三种情形，其每种情形的最后一局肯定是甲队胜 ‎①3：0，概率为P1=（）3=；‎ ‎②3：1，概率为P2=C（）2×（1﹣）×=；‎ ‎③3：2，概率为P3=C（）2×（1﹣）2×=‎ ‎∴甲队3：0，3：1，3：2胜利的概率：．‎ ‎（2）乙队得分X，则X的取值可能为0，1，2，3．‎ 由（1）知P（X=0）=P1+P2=；‎ P（X=1）=P3=；‎ P（X=2）=C（1﹣）2×（）2×=；‎ P（X=3）=（1﹣）3+C（1﹣）2×（）×=；‎ 则X的分布列为 X ‎3‎ ‎2‎ ‎1‎ ‎0‎ P E（X）=3×+2×+1×+0×=．‎ ‎【点评】本题主要考查了相互独立事件的概率乘法公式，以及离散型随机变量的期望与分布列，同时考查了分类讨论的数学思想，属于中档题．‎ ‎　‎ ‎20．（12分）设等差数列{an}的前n项和为Sn，且S4=4S2，a2n=2an+1．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）设数列{bn}的前n项和为Tn且（λ为常数）．令cn=b2n（n∈N*）求数列{cn}的前n项和Rn．‎ ‎【分析】（1）设出等差数列的首项和公差，由已知条件列关于首项和公差的方程组，解出首项和公差后可得数列{an}的通项公式；‎ ‎（2）把{an}的通项公式代入，求出当n≥2时的通项公式，然后由cn=b2n得数列{cn}的通项公式，最后利用错位相减法求其前n项和．‎ ‎【解答】解：（1）设等差数列{an}的首项为a1，公差为d，由a2n=2an+1，取n=1，得a2=2a1+1，即a1﹣d+1=0①‎ 再由S4=4S2，得，即d=2a1②‎ 联立①、②得a1=1，d=2．‎ 所以an=a1+（n﹣1）d=1+2（n﹣1）=2n﹣1；‎ ‎（2）把an=2n﹣1代入，得，则．‎ 所以b1=T1=λ﹣1，‎ 当n≥2时，=．‎ 所以，．‎ Rn=c1+c2+…+cn=③‎ ‎④‎ ‎③﹣④得：=‎ 所以；‎ 所以数列{cn}的前n项和．‎ ‎【点评】‎ 本题考查了等差数列的通项公式，考查了数列的求和，训练了错位相减法，考查了学生的计算能力，属中档题．‎ ‎　‎ ‎21．（13分）设函数．‎ ‎（1）求f（x）的单调区间及最大值；‎ ‎（2）讨论关于x的方程|lnx|=f（x）根的个数．‎ ‎【分析】（1）利用导数的运算法则求出f′（x），分别解出f′（x）＞0与f′（x）＜0即可得出单调区间及极值与最值；‎ ‎（2）分类讨论：①当0＜x≤1时，令u（x）=﹣lnx﹣﹣c，②当x≥1时，令v（x）=lnx﹣．利用导数分别求出c的取值范围，即可得出结论．‎ ‎【解答】解：（1）∵=，解f′（x）＞0，得；解f′（x）＜0，得．‎ ‎∴函数f（x）的单调递增区间为；单调递减区间为．‎ 故f（x）在x=取得最大值，且．‎ ‎（2）函数y=|lnx|，当x＞0时的值域为[0，+∞）．如图所示：‎ ‎①当0＜x≤1时，令u（x）=﹣lnx﹣﹣c，‎ c==g（x），‎ 则=．‎ 令h（x）=e2x+x﹣2x2，则h′（x）=2e2x+1﹣4x＞0，∴h（x）在x∈（0，1]单调递增，‎ ‎∴1=h（0）＜h（x）≤h（1）=e2﹣1．‎ ‎∴g′（x）＜0，∴g（x）在x∈（0，1]单调递减．‎ ‎∴c．‎ ‎②当x≥1时，令v（x）=lnx﹣，得到c=lnx﹣=m（x），‎ 则=＞0，‎ 故m（x）在[1，+∞）上单调递增，∴c≥m（1）=．‎ 综上①②可知：当时，方程|lnx|=f（x）无实数根；‎ 当时，方程|lnx|=f（x）有一个实数根；‎ 当时，方程|lnx|=f（x）有两个实数根．‎ ‎【点评】本题综合考查了利用导数研究函数的单调性、极值最值、数形结合的思想方法、分类讨论的思想方法等基础知识与基本技能，考查了推理能力和计算能力及其化归思想方法．‎ ‎　‎ ‎22．（13分）椭圆C：的左右焦点分别是F1，F2，离心率为，过F1且垂直于x轴的直线被椭圆C截得的线段长为1．‎ ‎（1）求椭圆C的方程；‎ ‎（2）点P是椭圆C上除长轴端点外的任一点，连接PF1，PF2，设∠F1PF2的角平分线PM交C的长轴于点M（m，0），求m的取值范围；‎ ‎（3）在（2）的条件下，过点P作斜率为k的直线l，使得l与椭圆C有且只有一个公共点，设直线PF1，PF2的斜率分别为k1，k2，若k≠0，试证明为定值，并求出这个定值．‎ ‎【分析】（1）把﹣c代入椭圆方程得，解得，由已知过F1‎ 且垂直于x轴的直线被椭圆C截得的线段长为1，可得．再利用，及a2=b2+c2即可得出；‎ ‎（2）设|PF1|=t，|PF2|=n，由角平分线的性质可得，利用椭圆的定义可得t+n=2a=4，消去t得到，化为，再根据a﹣c＜n＜a+c，即可得到m的取值范围；‎ ‎（3）设P（x0，y0），不妨设y0＞0，由椭圆方程，取，利用导数即可得到切线的斜率，再利用斜率计算公式即可得到k1，k2，代入即可证明结论．‎ ‎【解答】解：（1）把﹣c代入椭圆方程得，解得，‎ ‎∵过F1且垂直于x轴的直线被椭圆C截得的线段长为1，∴．‎ 又，联立得解得，‎ ‎∴椭圆C的方程为．‎ ‎（2）如图所示，设|PF1|=t，|PF2|=n，‎ 由角平分线的性质可得，‎ 又t+n=2a=4，消去t得到，化为，‎ ‎∵a﹣c＜n＜a+c，即，也即，解得．‎ ‎∴m的取值范围；．‎ ‎（3）证明：设P（x0，y0），‎ 不妨设y0＞0，由椭圆方程，‎ 取，则=，‎ ‎∴k==．‎ ‎∵，，‎ ‎∴=，‎ ‎∴==﹣8为定值．‎ ‎【点评】本题综合考查了椭圆的定义、标准方程及其性质、角平分线的性质、利用导数的几何意义研究切线、斜率计算公式等基础知识，考查了推理能力、分类讨论的思想方法、计算能力、分析问题和解决问题的能力．‎ ‎　‎