2020高中数学 课时分层作业14 空间向量及其加减运算 空间向量的数乘运算 新人教A版选修2-1

2020高中数学 课时分层作业14 空间向量及其加减运算 空间向量的数乘运算 新人教A版选修2-1

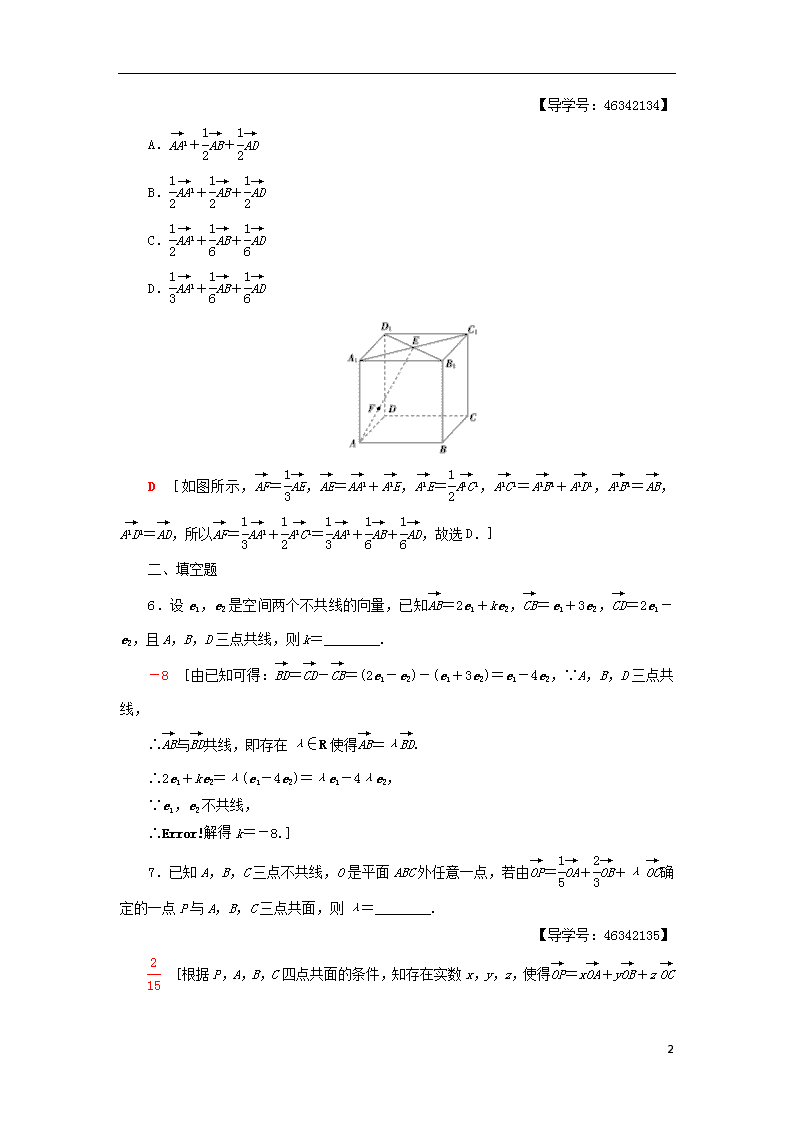
课时分层作业(十四) 空间向量及其加减运算 空间向量的数乘运算 ‎(建议用时：40分钟)‎ ‎[基础达标练]‎ 一、选择题 ‎1．下列关于空间向量的命题中，正确命题的个数是(　　)‎ ‎①任一向量与它的相反向量不相等；‎ ‎②长度相等、方向相同的两个向量是相等向量；‎ ‎③平行且模相等的两个向量是相等向量；‎ ‎④若a≠b，则|a|≠|b|；‎ ‎⑤两个向量相等，则它们的起点与终点相同．‎ A．0　　 B．‎1　‎　　　C．2　　　　D．3‎ B　[因为零向量与它的相反向量相等，所以①不正确；根据向量的定义，知长度相等、方向相同的两个向量是相等向量，②正确；平行且模相等的两个向量可能是相等向量，也可能是相反向量，③不正确；当a＝－b时，也有|a|＝|b|，④不正确；只要模相等、方向相同，两个向量就是相等向量，与向量的起点与终点无关，⑤不正确．综上可知只有②正确，故选B．]‎ ‎2．对于空间中任意三个向量a，b,‎2a－b，它们一定是(　　)‎ A．共面向量 B．共线向量 C．不共面向量 D．既不共线也不共面向量 A　[由共面向量定理易得答案A．]‎ ‎3．空间任意四个点A，B，C，D，则＋－等于(　　)‎ A． B． C． D． D　[＋－＝＋＝.]‎ ‎4．A，B，C不共线，对空间任意一点O，若＝＋＋，则P，A，B，C四点(　　)‎ A．不共面 B．共面 C．不一定共面 D．无法判断 B　[∵＋＋＝1，‎ ‎∴点P，A，B，C四点共面．]‎ ‎5．已知在长方形ABCDA1B‎1C1D1中，点E是A‎1C1的中点， 点F是AE的三等分点，且AF＝EF，则＝(　　) ‎ 6‎ ‎【导学号：46342134】‎ A．＋＋ B．＋＋ C．＋＋ D．＋＋ D　[如图所示，＝，＝＋，＝，＝＋，＝，＝，所以＝＋＝＋＋，故选D．]‎ 二、填空题 ‎6．设e1，e2是空间两个不共线的向量，已知＝2e1＋ke2，＝e1＋3e2，＝2e1－e2，且A，B，D三点共线，则k＝________.‎ ‎－8　[由已知可得：＝－＝(2e1－e2)－(e1＋3e2)＝e1－4e2，∵A，B，D三点共线，‎ ‎∴与共线，即存在λ∈R使得＝λ.‎ ‎∴2e1＋ke2＝λ(e1－4e2)＝λe1－4λe2，‎ ‎∵e1，e2不共线，‎ ‎∴解得k＝－8.]‎ ‎7．已知A，B，C三点不共线，O是平面ABC外任意一点，若由＝＋＋λ确定的一点P与A，B，C三点共面，则λ＝________. ‎ ‎【导学号：46342135】‎ 　[根据P，A，B，C四点共面的条件，知存在实数x，y，z，使得＝x＋y＋z成立，其中x＋y＋z＝1，于是＋＋λ＝1，所以λ＝.]‎ 6‎ ‎8．在空间四边形ABCD中，E，F分别是AB，CD的中点，则和＋的关系是________．(填“平行”、“相等”或“相反”)‎ 平行　[设G是AC的中点，则＝＋＝＋＝(＋)‎ 从而∥(＋)．]‎ 三、解答题 ‎9．已知四边形ABCD为正方形，P是四边形ABCD所在平面外一点，P在平面ABCD上的射影恰好是正方形ABCD的中心O，Q是CD的中点．求下列各式中x，y的值．‎ ‎(1)＝＋x＋y；‎ ‎(2)＝x＋y＋.‎ ‎[解]　如图所示，‎ ‎(1)∵＝－ ‎＝－(＋)‎ ‎＝－－，‎ ‎∴x＝y＝－.‎ ‎(2)∵＋＝2，‎ ‎∴＝2－.‎ 又∵＋＝2，‎ ‎∴＝2－.‎ 从而有＝2－(2－)‎ ‎＝2－2＋.‎ ‎∴x＝2，y＝－2.‎ ‎10．在长方体ABCDA1B‎1C1D1中，M为DD1的中点，点N在AC上，且AN∶NC 6‎ ‎＝2∶1，求证：与，共面. ‎ ‎【导学号：46342136】‎ ‎[证明]　∵＝－，‎ ＝＋＝－，‎ ＝＝(＋)，‎ ‎∴＝－ ‎＝(＋)－ ‎＝(－)＋(－)‎ ‎＝＋，‎ ‎∴与，共面．‎ ‎[能力提升练]‎ ‎1．如图3111所示，已知A，B，C三点不共线，P为平面ABC内一定点，O为平面ABC外任一点，则下列能表示向量的为(　　)‎ 图3111‎ A．＋2＋2　　 B．－3－2 C．＋3－2 D．＋2－3 C　[因为A，B，C，P四点共面，所以可设＝x＋y，即＝＋x＋y，由图可知x＝3，y＝－2，故选C．]‎ ‎2．如图3112是一平行六面体ABCDA1B‎1C1D1，E为BC延长线上一点，＝2，则＝(　　)‎ 6‎ ‎ ‎ 图3112‎ A．＋＋ B．＋－ C．＋－ D．＋－ B　[取BC的中点F，连接A‎1F，则A1D1FE，所以四边形A1D1EF是平行四边形，所以A‎1FD1E，所以＝.又＝＋＋＝－＋＋，所以＝＋－，故选B．]‎ ‎3．已知A，B，C三点共线，则对空间任一点O，存在三个不为0的实数λ，m，n，使λ＋m＋n＝0，那么λ＋m＋n的值为________．‎ ‎0　[由λ＋m＋n＝0得＝－－ 由A，B，C三点共线知－－＝1，则λ＋m＋n＝0.]‎ ‎4．如图3113，O为△ABC所在平面外一点，M为BC的中点，若＝λ与＝＋＋同时成立，则实数λ的值为________．‎ 图3113‎ 6‎ 　[＝＋＝＋λ＝＋(＋)＝＋(－＋－)＝(1－λ)＋＋，所以1－λ＝，＝，解得λ＝.]‎ ‎5．如图3114所示，平行六面体ABCDA1B‎1C1D1中，E，F分别在B1B和D1D上，且BE＝BB1，DF＝DD1.‎ 图3114‎ ‎(1)证明：A，E，C1，F四点共面；‎ ‎(2)若＝x＋y＋z，求x＋y＋z的值. ‎ ‎【导学号：46342137】‎ ‎[解]　(1)因为＝＋＋＝＋＋＋＝＋＝＋＝＋，‎ 所以A，E，C1，F四点共面．‎ ‎(2)因为＝－＝＋－(＋)＝＋－－＝－＋＋，‎ 所以x＝－1，y＝1，z＝，‎ 所以x＋y＋z＝.‎ 6‎