湖南省江西省2020届高三普通高中名校联考信息卷（压轴卷一）文科数学试题

湖南省江西省2020届高三普通高中名校联考信息卷（压轴卷一）文科数学试题

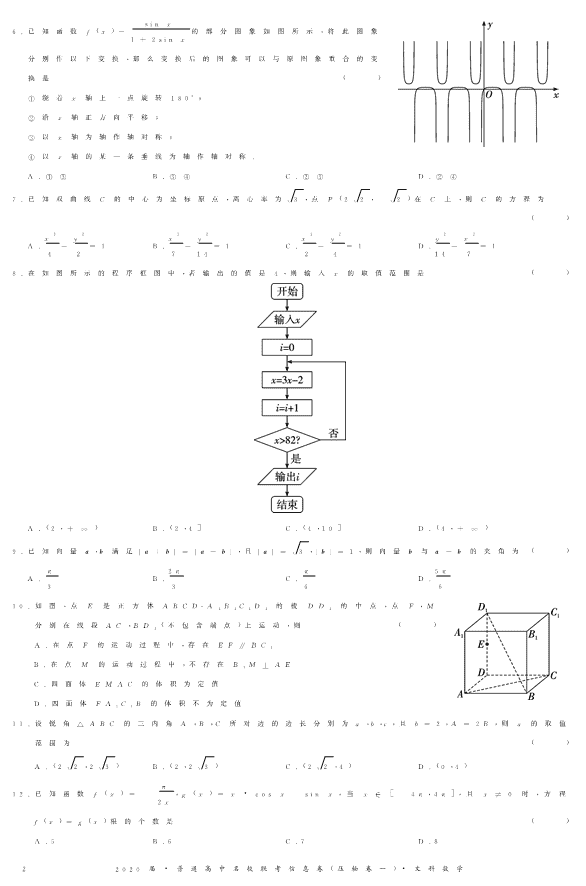
书书书 ２０２０届·普通高中名校联考信息卷（压轴卷一） （高考研究卷） 文科数学 考生注意： 　１．本试卷共１５０分，考试时间１２０分钟． 　２．请将答案填在答题卡上． 　一、选择题：本大题共１２小题，每小题５分，共６０分．在每小题给出的四个选项中，只有一项是 符合题目要求的． １．设函数狔＝ ４－狓槡 ２ 的定义域为犃，函数狔＝ｌｎ（２－狓）的定义域为犅，则犃∩犅＝ （　　） Ａ．（－∞，２） Ｂ．（０，２） Ｃ．｛２｝ Ｄ．［－２，２） ２．若复数狕满足（１＋ｉ）狕＝１＋２ｉ，则｜珔狕｜＝ （　　） Ａ．槡２ ２ Ｂ．３ ２ Ｃ．槡１０ ２ Ｄ．１ ２ ３．ｓｉｎ１６３°ｓｉｎ２２３°＋ｓｉｎ２５３°ｓｉｎ３１３°等于 （　　） Ａ．－１ ２ Ｂ．１ ２ Ｃ．－槡３ ２ Ｄ．槡３ ２ ４．《聊斋志异》中有：“挑水砍柴不堪苦，请归但求穿墙术”．在数学中，我们称形如以下形式的等 式具有“穿墙术”：２槡２ ３ ＝ ２槡２ ３ ，３槡３ ８ ＝ ３槡３ ８ ，４ ４槡１５＝ ４４槡１５，则按照以上规律，若 犿槡犿 狀 ＝ 犿槡犿 狀 具有“穿墙术”，则犿，狀满足的关系式为 （　　） Ａ．狀＝２犿－１ Ｂ．狀＝２（犿－１） Ｃ．狀＝（犿－１）２ Ｄ．狀＝犿２－１ ５．某四棱锥的三视图如图所示，记犛为此棱锥所有棱的长度的集合，则 （　　） Ａ．槡２ ２犛，且 槡２ ３犛 Ｂ．槡２ ２犛，且 槡２ ３∈犛 Ｃ．槡２ ２∈犛，且 槡２ ３犛 Ｄ．槡２ ２∈犛，且 槡２ ３∈犛 １２０２０届·普通高中名校联考信息卷（压轴卷一）·文科数学 ６．已知函数犳（狓）＝ ｓｉｎ狓 １＋２ｓｉｎ狓的部分图象如图所示，将此图象 分别作以下变换，那么变换后的图象可以与原图象重合的变 换是 （　　） ①绕着狓轴上一点旋转１８０°； ②沿狓轴正方向平移； ③以狓轴为轴作轴对称； ④以狓轴的某一条垂线为轴作轴对称． Ａ．①③ Ｂ．③④ Ｃ．②③ Ｄ．②④ ７．已知双曲线犆的中心为坐标原点，离心率为槡３，点犘（槡２ ２， 槡－ ２）在犆上，则犆的方程为 （　　） Ａ．狓２ ４－狔２ ２＝１ Ｂ．狓２ ７－狔２ １４＝１ Ｃ．狓２ ２－狔２ ４＝１ Ｄ．狔２ １４－狓２ ７＝１ ８．在如图所示的程序框图中，若输出的值是４，则输入狓的取值范围是 （　　） Ａ．（２，＋∞） Ｂ．（２，４］ Ｃ．（４，１０］ Ｄ．（４，＋∞） ９．已知向量犪，犫满足｜犪＋犫｜＝｜犪－犫｜，且｜犪｜ 槡＝ ３，｜犫｜＝１，则向量犫与犪－犫的夹角为 （　　） Ａ．π ３ Ｂ．２π ３ Ｃ．π ６ Ｄ．５π ６ １０．如图，点犈 是正方体犃犅犆犇犃１犅１犆１犇１ 的棱 犇犇１ 的中点，点犉，犕 分别在线段犃犆，犅犇１（不包含端点）上运动，则 （　　） Ａ．在点犉 的运动过程中，存在犈犉∥犅犆１ Ｂ．在点 犕 的运动过程中，不存在犅１犕⊥犃犈 Ｃ．四面体犈犕犃犆的体积为定值 Ｄ．四面体犉犃１犆１犅 的体积不为定值 １１．设锐角△犃犅犆的三内角犃，犅，犆所对边的边长分别为犪，犫，犮，且犫＝２，犃＝２犅，则犪的取值 范围为 （　　） Ａ．（槡２ ２，槡２ ３） Ｂ．（２，槡２ ３） Ｃ．（槡２ ２，４） Ｄ．（０，４） １２．已知函数犳（狓）＝－ π ２狓，犵（狓）＝狓·ｃｏｓ狓－ｓｉｎ狓，当狓∈［－４π，４π］，且狓≠０时，方程 犳（狓）＝犵（狓）根的个数是 （　　） Ａ．５ Ｂ．６ Ｃ．７ Ｄ．８ ２ ２０２０届·普通高中名校联考信息卷（压轴卷一）·文科数学 二、填空题：本大题共４小题，每小题５分，共２０分．把答案填在答题卡相应位置上． １３．若函数犳（狓）＝ ｌｇ狓，狓＞０， 犪狓＋犫，狓≤０烅烄 烆 ，且犳（０）＝３，犳（－１）＝４，则犳（犳（－３））＝　　　　　． １４．将一颗骰子先后投掷两次分别得到点数犪，犫，则直线犪狓＋犫狔＝０与圆（狓－２）２＋狔２＝２有公 共点的概率为　　　　　． １５．圆锥底面半径为１，高为 槡２ ２，点犘 是底面圆周上一点，则一动点从点犘 出发，绕圆锥侧面 一圈之后回到点犘，则绕行的最短距离是　　　　　． １６．在党中央的正确指导下，通过全国人民的齐心协力，特别是全体一线医护人员的奋力救治， 二月份“新冠肺炎”疫情得到了控制．下图是国家卫健委给出的全国疫情通报，甲、乙两个省 份从２月７日到２月１３日一周的新增“新冠肺炎”确诊人数的折线图如下： 根据图中甲、乙两省的数字特征进行比对，通过比较把你得到最重要的两个结论写在答题 卡指定的空白处． ① 　． ② 　． 三、解答题：共７０分，解答应写出文字说明、证明过程或演算步骤．第１７～２１题为必考题，每个 试题考生都必须作答．第２２、２３题为选考题，考生根据要求作答． （一）必考题：共６０分． １７．（本小题满分１２分） 设犛狀 为数列 犪｛ ｝狀 的前狀 项和，已知犪３＝７，犪狀＝２犪狀－１＋犪２－２（狀≥２）． （１）证明：数列 犪狀｛ ｝＋１ 为等比数列； （２）求数列 犪｛ ｝狀 的通项公式，并判断狀，犪狀，犛狀 是否成等差数列？ ３２０２０届·普通高中名校联考信息卷（压轴卷一）·文科数学 １８．（本小题满分１２分） 由于受到网络电商的冲击，某品牌的高压锅在线下的销售受到影响，承受了一定的经济损 失，现将犃 地区２００家实体店该品牌高压锅的月经济损失统计如图所示． （１）求犪的值； （２）求犃 地区２００家实体店该品牌高压锅的月经济损失的众数以及中位数； （３）不经过计算，直接给出犃 地区２００家实体店经济损失的平均数珚狓与６０００的大小关系． １９．（本小题满分１２分） 如图，在多面体 犃犅犆犇犈犉 中，底面 犃犅犆犇 是正方形，梯形 犃犇犈犉⊥底面犃犅犆犇，且犃犉＝犈犉＝犇犈＝１ ２犃犇． （１）证明平面犃犅犉⊥平面犆犇犉； （２）平面犆犇犉 将多面体犃犅犆犇犈犉 分成两部分，求两部分的体 积比． ４ ２０２０届·普通高中名校联考信息卷（压轴卷一）·文科数学 ２０．（本小题满分１２分） 已知椭圆犆：狓２ 犪２＋狔２ 犫２＝１（犪＞犫＞０）的短轴长为 槡２ ２，离心率为槡３ ２． （１）求椭圆犆的标准方程； （２）直线犾平行于直线狔＝犫 犪狓，且与椭圆犆 交于犃，犅 两个不同的点，若!犃犗犅 为钝角，求 直线犾在狓 轴上的截距犿 的取值范围． ２１．（本小题满分１２分） 已知函数犳（狓）＝ｌｎ狓＋犪 狓（犪∈犚）． （１）讨论函数犳（狓）的单调性； （２）令犵（犪）＝犪（犽－５）－２ 犪 ，若对任意的狓＞０，犪＞０，恒有犳（狓）≥犵（犪）成立，求实数犽的最 大整数． ５２０２０届·普通高中名校联考信息卷（压轴卷一）·文科数学 （二）选考题：共１０分．请考生在第２２、２３题中任选一题作答．如果多做，则按所做的第一题计 分． ２２．（本小题满分１０分）［选修４－４：坐标系与参数方程］ 在直角坐标系狓犗狔中，曲线犆１ 的参数方程为 狓＝１＋ｃｏｓα， 狔＝ｓｉｎ｛ α （α为参数），曲线犆２：狓２ ２＋狔２ ＝１． （１）在以犗 为极点，狓轴的正半轴为极轴的极坐标系中，求犆１，犆２ 的极坐标方程； （２）射线θ＝π ６（ρ≥０）与犆１ 的异于极点的交点为犃，与犆２ 的交点为犅，求｜犃犅｜． ２３．（本小题满分１０分）［选修４－５：不等式选讲］ 已知函数犳（狓）＝１ ３｜狓－犪｜（犪∈犚）． （１）当犪＝２时，解不等式｜狓－１ ３｜＋犳（狓）≥１； （２）设不等式｜狓－１ ３｜＋犳（狓）≤狓的解集为犕，若［１ ３，１ ２］犕，求实数犪的取值范围． ６ ２０２０届·普通高中名校联考信息卷（压轴卷一）·文科数学