- 2021-06-19 发布 |
- 37.5 KB |
- 8页

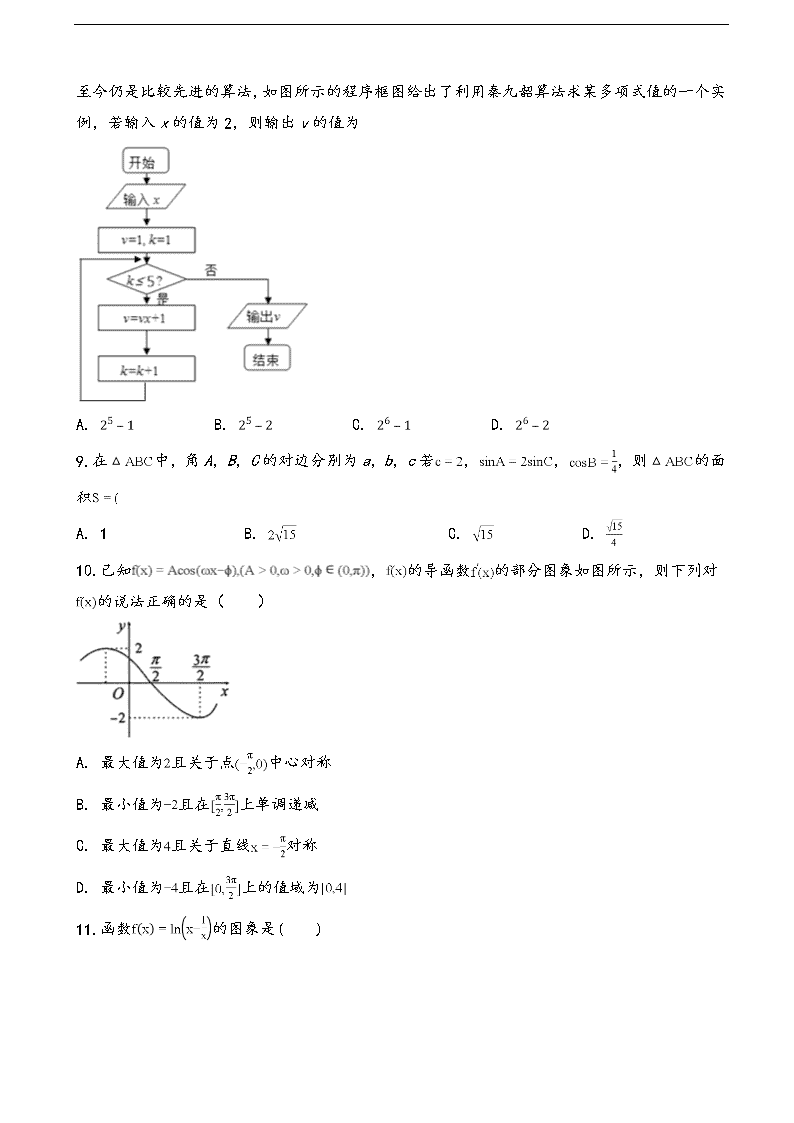

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届安徽省肥东县高级中学高三1月调研考试数学(文)试题
2020届高三年级1月调研 文科数学试题 注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。 2.作答时,务必将答案写在答题卡上,写在本试卷及草稿纸上无效。 3.考试结束后,将本试卷和答题卡一并交回。 第I卷 选择题(共60分) 一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。) 1.=( ) A. ﹣1 B. ﹣i C. 1 D. i 2.已知Sn为等差数列{an}的前n项和,a1=1,公差为d,则“﹣1<d<0”是“S22+S52<26”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 3.设函数是定义在上的偶函数,且,若,则 A. B. C. D. 4.已知向量的夹角为,且,则( ) A. B. 2 C. D. 84 5.设函数(),则是( ) A. 最小正周期为的奇函数 B. 最小正周期为的偶函数 C. 最小正周期为的奇函数 D. 最小正周期为的偶函数 6.已知,,设,,,则的大小关系是( ) A. B. C. D. 7.已知是等差数列,是正项等比数列,且,,,,则 A. 2274 B. 2074 C. 2226 D. 2026 8.秦九韶是我国宋时期的数学家,他在所著的数书九章 中提出的多项式求值的秦九韶算法至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为 A. B. C. D. 9.在中,角A,B,C的对边分别为a,b,c若,,,则的面积 A. 1 B. C. D. 10.已知,的导函数的部分图象如图所示,则下列对的说法正确的是( ) A. 最大值为且关于点中心对称 B. 最小值为且在上单调递减 C. 最大值为且关于直线对称 D. 最小值为且在上的值域为 11.函数的图象是( ) 12.设函数的导函数为,且,则 ( ) A. B. C. D. 第II卷 非选择题(共90分) 二、填空题(本大题共4小题,每小题5分,共20分) 13.已知向量,则___________. 14.已知等比数列的前n项和为,若,,则=_______. 15.已知函数 , 则满足的的取值范围是________. 16.函数的单调减区间为______. 三、解答题(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。) 17. (本题10分) 已知设成立; 指数函数为增函数,如果“”为真,“”为假,求实数的取值范围. 18. (本题12分) 已知等差数列的前项和为,且,. (Ⅰ)求数列的通项公式; (Ⅱ)若数列满足,,求数列的前项和. 19. (本题12分) 已知分别是三个内角的对边,且. (1)求角的值. (2)若,点在边上,,求的长. 20. (本题12分) 已知函数. (1)若函数的图象与轴无交点,求的取值范围; (2)若函数在上存在零点,求的取值范围. 21. (本题12分) 已知函数 Ⅰ求的最小正周期; Ⅱ若在区间上单调递增,求实数m的最大值. 22. (本题12分) 已知函数,. (1)若是的极值点, 求并讨论的单调性; (2)若时,,求的取值范围. 参考答案 1.A 2.B 3.D 4.C 5.B 6.A 7.A 8.C 9.C 10.D 11.B 12.C 13. 14.1 15.. 16. 17.或. 解 由题意可得:若为真,则;若为真,则,原问题等价于与一真一假,结合计算结果分类讨论可得实数的取值范围是或. 试题解析: 若为真:对, 恒成立, 设,配方得, 所以在上的最小值为, 所以,解得,所以为真时: ; 若为真: , 因为”为真,“”为假,所以与一真一假, 当真假时,所以, 当假真时,所以, 综上所述,实数的取值范围是或. 18.(Ⅰ).(Ⅱ) 解(Ⅰ) ,∴ ,∴ 则 . (Ⅱ)由(Ⅰ)可知, , - = = ∴ 19.(1);(2) 解(1)中,,∴, ∴, ∴,∴,∴; (2)如图所示, 设, ∴; 由余弦定理得,…① ,…② 由①②解得,即的长为. 20.(1);(2). 解 (1)若函数y=f(x)的图象与x轴无交点, 则方程f(x)=0的根的判别式Δ<0,即16-4(a+3)<0, 解得a>1. 故a的取值范围为a>1. (2)因为函数f(x)=x2-4x+a+3图象的对称轴是x=2, 所以y=f(x)在[-1,1]上是减函数. 又y=f(x)在[-1,1]上存在零点, 所以,即, 解得-8≤a≤0. 故实数a的取值范围为-8≤a≤0. 21.(Ⅰ)最小正周期为(Ⅱ) 解Ⅰ函数, , , 所以:函数的最小正周期为. Ⅱ由于:, 令:, 解得:, 当时,, 在区间上单调递增, 故:, 所以:m的最大值为. 22.解(1)求出原函数的导函数,结合求得,代入导函数,得到,再由在上单调递增,且,可得当时,,单调递减;当时,,单调递增;(2)由 ,得,令,利用二次求导可得其最小值,则..的范围可求. (1),. 因为是的极值点, 所以,可得. 所以,. 因为在上单调递增,且时,, 所以时,,,单调递减; 时, ,,单调递增. 故在上单调递减,在上单调递增. (2)由得, 因为,所以. 设, 则. 令, 则, 显然在内单调递减,且, 所以时,,单调递减, 则,即, 所以在内单减,从而. 所以.查看更多