【数学】2018届一轮复习北师大版第六章不等式推理与证明第三节二元一次不等式组与简单的线性规划问题教案
第三节 二元一次不等式(组)与简单的线性规划问题
☆☆☆2017考纲考题考情☆☆☆
考纲要求
真题举例
命题角度
1.会从实际情境中抽象出二元一次不等式组;
2.了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组;
3.会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决。
2016,全国卷Ⅰ,16,5分(线性规划的实际应用)
2016,全国卷Ⅲ,13,5分(求最优解)
2015,全国卷Ⅰ,15,5分(非线性规划求最值)
2015,全国卷Ⅱ,14,5分(求目标函数最值)
2014,全国卷Ⅰ,9,5分(求目标函数最值)
线性规划问题是高考命题的热点,难度中等偏下,主要考查可行域的画法、目标函数最值的求法、由最优解(可行域)情况确定参数的范围,以及数形结合的思想。
微知识 小题练
自|主|排|查
1.二元一次不等式(组)表示的平面区域
不等式
表示区域
Ax+By+C>0
直线Ax+By+C=0某一侧的所有点组成的平面区域
不包括边界直线
Ax+By+C≥0
包括边界直线
不等式组
各个不等式所表示平面区域的公共部分
2.线性规划中的有关概念
名称
意义
约束条件
由变量x,y组成的不等式(组)
线性约束条件
由x,y的一次不等式组成的不等式(组)
目标函数
关于x,y的函数解析式,如z=x+2y
线性目标函数
关于x,y的一次解析式
可行解
满足线性约束条件的解(x,y)
可行域
所有可行解组成的集合
最优解
使目标函数取得最大值或最小值的可行解
线性规划问题
在线性约束条件下
求线性目标函数的
最大值或最小值问题
3.确定二元一次不等式(组)表示的平面区域的方法
确定二元一次不等式(组)表示的平面区域时,经常采用“直线定界,特殊点定域”的方法。
(1)直线定界,不等式含等号,直线在区域内,不含等号,直线不在区域内。
(2)特殊点定域,在直线上方(下方)取一点,代入不等式成立,则区域就为上方(下方),否则就是下方(上方)。特别地,当C≠0时,常把原点作为测试点;当C=0时,常选点(1,0)或者(0,1)作为测试点。
微点提醒
1.判断二元一次不等式表示的平面区域的常用结论
把Ax+By+C>0或Ax+By+C<0化为y>kx+b或y
kx+b则区域为直线Ax+By+C=0上方。
(2)若y0,则直线过可行域且在y轴上截距最大时,z值最大,在y轴上截距最小时,z值最小;若b<0,则相反。
小|题|快|练
一 、走进教材
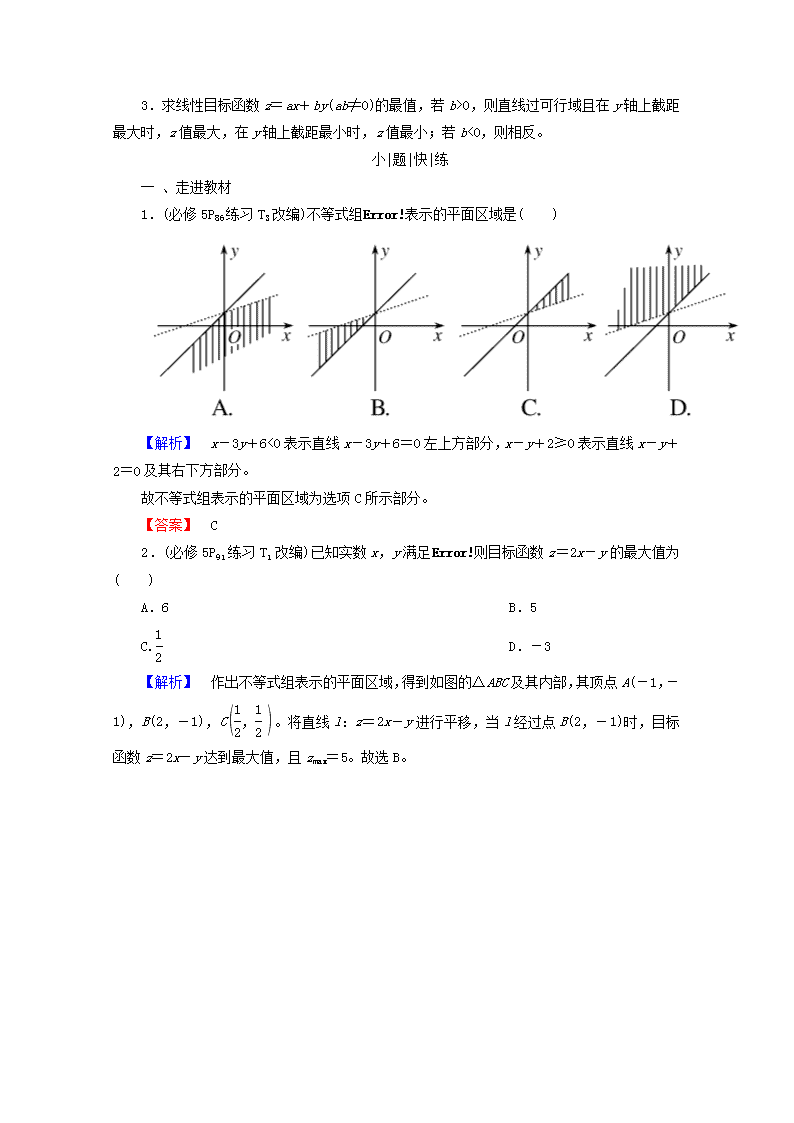
1.(必修5P86练习T3改编)不等式组表示的平面区域是( )
【解析】 x-3y+6<0表示直线x-3y+6=0左上方部分,x-y+2≥0表示直线x-y+2=0及其右下方部分。
故不等式组表示的平面区域为选项C所示部分。
【答案】 C
2.(必修5P91练习T1改编)已知实数x,y满足则目标函数z=2x-y的最大值为( )
A.6 B.5
C. D.-3
【解析】 作出不等式组表示的平面区域,得到如图的△ABC及其内部,其顶点A(-1,-1),B(2,-1),C。将直线l:z=2x-y进行平移,当l经过点B(2,-1)时,目标函数z=2x-y达到最大值,且zmax=5。故选B。
【答案】 B
二、双基查验
1.点(3,1)和(-4,6)在直线3x-2y+a=0的两侧,则a的取值范围是( )
A.a<-7,或a>24 B.-7<a<24
C.a=-7,或a=24 D.以上都不对
【解析】 点(3,1)和(-4,6)在直线3x-2y+a=0的两侧,说明将这两点坐标代入3x-2y+a后,符号相反,所以(9-2+a)(-12-12+a)<0,解之得-7<a<24。故选B。
【答案】 B
2.不等式组所表示的平面区域的面积等于( )
A. B.
C. D.
【解析】 不等式组表示的平面区域如图所示。由得交点A的坐标为(1,1)。
又B,C两点的坐标为(0,4),。
故S△ABC=××1=。故选C。
【答案】 C
3.(2016·山东高考)若变量x,y满足则x2+y2的最大值是( )
A.4 B.9
C.10 D.12
【解析】 作出不等式组所表示的平面区域如图中阴影部分所示,设P(x,y)为平面区域内任意一点,则x2+y2表示|OP|2。显然,当点P与点A重合时,|OP|2即x2+y2取得最大值。由,解得,故A(3,-1)。所以x2+y2的最大值为32+(-1)2=10。故选C。
【答案】 C
4.(2016·全国卷Ⅲ)若x,y满足约束条件则z=x+y的最大值为________。
【解析】 约束条件对应的平面区域是以点、(0,1)和(-2,-1)为顶点的三角形,当目标函数y=-x+z经过点时,z取得最大值。
【答案】
5.已知实数x,y满足不等式组目标函数z=y-ax(a∈R)。若z取最大值时的唯一最优解是(1,3),则实数a的取值范围是__________。
【解析】 如图,依题意,直线x+y-4=0与x-y+2=0交于A(1,3),此时目标函数取最大值,故a>1。
【答案】 (1,+∞)
微考点 大课堂
考点一
二元一次不等式(组)表示平面区域
【典例1】 设动点P(x,y)在区域Ω:上,过点P任作直线l,设直线l与区域Ω的公共部分为线段AB,则以AB为直径的圆的面积的最大值为( )
A.π B.2π
C.3π D.4π
【解析】 作出不等式组所表示的可行域如图中阴影部分所示,则根据图形可知,以AB为直径的圆的面积的最大值S=π×2=4π。故选D。
【答案】 D
反思归纳 1.“直线定界,特殊点定域”,即先作直线,再取特殊点并代入不等式组。若满足不等式组,则不等式(组)表示的平面区域为直线与特殊点同侧的那部分区域;否则就对应与特殊点异侧的平面区域。
2.当不等式中带等号时,边界为实线;不带等号时,边界应画为虚线,特殊点常取原点。
【变式训练】 (2016·包头模拟)已知约束条件表示面积为1的直角三角形区域,则实数k
的值为( )
A.1 B.-1
C.0 D.-2
【解析】 作出不等式组
对应的平面区域,如图:
要使阴影部分为直角三角形,
当k=0时,此三角形的面积为×3×3=≠1,所以不成立,所以k>0,则必有BC⊥AB,
因为x+y-4=0的斜率为-1,
所以直线kx-y=0的斜率为1,即k=1。
故选A。
【答案】 A
考点二
求目标函数的最值………………多维探究
角度一:线性目标函数的最值
【典例2】 (2016·全国卷Ⅱ)若x,y满足约束条件则z=x-2y的最小值为________。
【解析】 解法一:作出可行域,如图中阴影部分所示,由z=x-2y得y=x-z,作直线y=x并平移,观察可知,当直线经过点A(3,4)时,zmin=3-2×4=-5。
解法二:因为可行域为封闭区域,所以线性目标函数的最值只可能在边界点处取得,易求得边界点分别为(3,4),(1,2),(3,0),依次代入目标函数可求得zmin=-5。
【答案】 -5
反思归纳 解决简单的线性规划问题的基本方法是图象法,即作出可行域后,要求目标函数z=ax+by的最值,先作出直线ax+by=0,然后平行移动直线ax+by=0,使它与可行域有公共点,可得到z的取值范围,则最值易得。在确定z的取值范围时应注意两点:一是斜率,即由z=ax+by(当b≠0时)得l:y=-x+,在确定z的取值范围时,需要比较斜率k=-与可行域边界的斜率的大小关系,从而确定直线l移动的范围;二是截距,即z的最值可由l在y轴上的截距来确定,但需要注意的是当b<0时,直线l在y轴上截距最大时,z不是取得最大值,而是取得最小值。
角度二:非线性目标函数的最值
【典例3】 实数x,y满足
(1)若z=,求z的最大值和最小值,并求z的取值范围;
(2)若z=x2+y2,求z的最大值与最小值,并求z的取值范围。
【解析】 由作出可行域,如图中阴影部分所示。
(1)z=表示可行域内任一点与坐标原点连线的斜率,
因此的范围为直线OB的斜率到直线OA的斜率(直线OA的斜率不存在,即zmax不存在)。
由得B(1,2),
∴kOB==2,即zmin=2,
∴z的取值范围是[2,+∞)。
(2)z=x2+y2表示可行域内的任意一点与坐标原点之间距离的平方。
因此x2+y2的值最小为|OA|2(取不到),最大值为|OB|2。
由得A(0,1),
∴|OA|2=()2=1,|OB|2=()2=5,
∴z的取值范围是(1,5]。
【答案】 (1)最大值不存在,最小值2,取值范围[2,+∞)
(2)最大值5,最小值无 取值范围(1,5]
【母题变式】 1.若z=,求z的取值范围。
【解析】 z=可以看作过点P(1,1)及(x,y)两点的直线的斜率。
∴z的取值范围是(-∞,0)。
【答案】 (-∞,0)
2.若z=x2+y2-2x-2y+3,求z的最大值、最小值。
【解析】 z=x2+y2-2x-2y+3
=(x-1)2+(y-1)2+1,
而(x-1)2+(y-1)2表示点P(1,1)与Q(x,y)的距离的平方|PQ|2,|PQ|=(0-1)2+(2-1)2=2,
|PQ|=2=,
∴zmax=2+1=3,zmin=+1=。
【答案】 最大值3,最小值
反思归纳 当目标函数是非线性的函数时,常利用目标函数的几何意义来解题,常见代数式的几何意义有:
1.表示点(x,y)与原点(0,0)的距离,表示点(x,y)与点(a,b)的距离;
2.表示点(x,y)与原点(0,0)连线的斜率,表示点(x,y)与点(a,b)连线的斜率。
角度三:线性规划中的参数问题
【典例4】 已知x,y满足约束条件若z=ax+y的最大值为4,则a=( )
A.3 B.2
C.-2 D.-3
【解析】 画出不等式组表示的平面区域如图阴影部分所示,若z=ax+y的最大值为4,则最优解为x=1,y=1或x=2,y=0,经检验知x=2,y=0符合题意,∴2a+0=4,此时a=2,故选B。
【答案】 B
反思归纳 求解线性规划中含参问题的基本方法有两种:一是把参数当成常数用,根据线性规划问题的求解方法求出最优解,代入目标函数确定最值,通过构造方程或不等式求解参数的值或取值范围;二是先分离含有参数的式子,通过观察的方法确定含参的式子所满足的条件,确定最优解的位置,从而求出参数。
角度四:线性规划的实际应用
【典例5】 (2016·全国卷Ⅰ)某高科技企业生产产品A和产品B需要甲、乙两种新型材料。生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时。生产一件产品A的利润为2 100元,生产一件产品B的利润为900元。该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________元。
【解析】 由题意,设产品A生产x件,产品B生产y件,则总利润z=2 100x+900y,约束条件为
作出不等式组表示的可行域如图阴影部分(包括边界)中的整数点所示。
由x∈N,y∈N,可知z取得最大值时的最优解为(60,100),所以zmax=2 100×60+900×100=216 000(元)。
【答案】 216 000
反思归纳 本题来源于人民教育出版社《数学必修5》(A版)第91页练习第2题:某厂拟生产甲、乙两种适销产品,每件销售收入分别为3 000元、2 000元。甲、乙产品都需要在A,B两种设备上加工,在每台A,B设备上加工1件甲设备所需工时分别为1 h、2 h,加工1件乙设备所需工时分别为2 h、1 h,A,B两种设备每月有效使用台时数分别为400 h和500 h。如何安排生产可使收入最大?
教材习题和高考真题的相同点都是以生产两种产品为背景,研究获利最大的问题;不同点是说法的过程不一样,数据进行变更,难度差不多,并且把解答题变为填空题。
微考场 新提升
1.不等式y≤3x+b所表示的区域恰好使点(3,4)不在此区域内,而点(4,4)在此区域内,则b的取值范围是( )
A.-8≤b≤-5 B.b≤-8或b>-5
C.-8≤b<-5 D.b≤-8或b≥-5
解析 由已知条件得⇒即-8≤b<-5。故选C。
答案 C
2.若变量x,y满足约束条件则z=2x+3y的最大值为( )
A.2 B.5
C.8 D.10
解析 作出如图中阴影部分所示的可行域,当直线y=-x+经过点A时z取得最大值。
由⇒,此时z=4×2+3×(-1)=5。
答案 B
3.(2017·株洲模拟)已知a>0,x,y满足约束条件若z=2x+y的最小值为1,则a=( )
A. B.
C.1 D.2
解析 如图所示,目标函数z=2x+y在点(1,-2a)处取得最小值,2×1-2a=1,解得a=。
答案 A
4.(2015·全国卷Ⅰ)若x,y满足约束条件则的最大值为________。
解析 作出可行域如图中阴影部分所示,
由可行域知,在点A(1,3)处,取得最大值3。
答案 3
5.(2016·郑州模拟)已知实数x,y满足设b=x-2y,若b的最小值为-2,则b的最大值为________。
解析 画出可行域,如图中阴影部分所示。由b=x-2y得,y=x-。易知在点(a,a)处b取最小值,故a-2a=-2,可得a=2。在点(2,-4)处b取最大值,于是b的最大值为2+8=10。
答案 10
微专题 巧突破
破解含参变量的线性规划问题
线性规划是沟通代数与几何的桥梁,是数形结合思想的集中体现。传统的线性规划问题主要研究的是在线性或非线性约束条件下求解目标函数的最值,就知识本身而言并不是难点。但是,近年来这类问题的命题设置在能力立意的命题思想指导下出现了新的动向:一方面将它与函数、方程、不等式、数列、平面向量、解析几何等知识交汇在一起;另一方面在这些问题背景中引进参变量,变换设问角度,提高思维强度,增加题目难度。下面我们对线性规划中参变量的新情景设置给出深度分析,帮助同学们走出思维误区,正确求解线性规划问题。
一、约束条件中设置的参变量
不等式组中含有参变量是线性规划命题的新动向之一,由于不能明确可行域的形状,因此增加了解题时画图分析的难度。求解这类问题时要有全局观念,结合目标函数逆向分析题意,整体把握解题的方向。
1.制约可行域的形状
【典例1】 已知实数x,y满足若该不等式组所表示的平面区域是一个面积为的直角三角形,则n的值是( )
A.- B.-2
C.2 D.
【解析】 不等式组所表示的平面区域如图中阴影部分所示。当直线x+my+n=0与直线x+2y=4垂直时,m=-,直线方程变为2x-y+2n=0,与x轴交点坐标为(-n,0),与直线x+2y=4交点的纵坐标为。此时三角形的面积为(4+n)·==,解得n=-(n=-舍去)。当直线x+my+n=0与x轴垂直或与直线x-y=1垂直时,求出的值均不符合条件。故选A。
【答案】 A
2.制约目标函数的最值
【典例2】 设变量x,y满足约束条件
其中a>1,若目标函数z=x+y的最大值为4,则a的值为________。
【解析】 根据题意作出不等式组表示的平面区域如图中阴影部分所示。令y=-x+z,则z的几何意义是直线y=-x+z的纵截距,则欲使z最大,只需使直线y=-x+z的纵截距最大即可。因为a>1,所以直线x+ay=7的斜率大于-1,于是当直线y=-x+z经过直线y=3x与直线x+ay=7的交点时,目标函数z取得最大值,最大值为。由题意得=4,解得a=2。故填2。
【答案】 2
二、目标式中设置的参变量
目标函数中设置参变量是线性规划命题的又一种新动向,旨在增加探索问题的动态性和开放性,考查考生的探究性思维能力。从目标函数的结论入手,对图形的动态分析和对变化过程中的相关量的准确定位是求解这类问题的主要思维方法。
1.求解目标式中的参数值
【典例3】 已知实数x,y满足约束条件若z=y-ax取得最大值的最优解不唯一,则实数a
的值为________。
【解析】 实数x,y满足约束条件表示的可行域如图所示,将z=y-ax化成斜截式为y=ax+z,要使z取得最大值的最优解不唯一,则y=ax+z在平移过程中与直线x+y-2=0重合或与直线2x-y+2=0重合,所以a=-1或2。故填-1或2。
【答案】 -1或2
【易错总结】 目标函数的最优解不唯一的问题,往往是指目标函数取得最值时所表示的直线过可行域中的一条边。据此,求解这类问题的方法可以让目标函数所表示的直线与可行域中的每条边界直线重合,从而求解。利用这种方法求解时,切记要进行检验,区分何时取得最大值的最优解不唯一,何时取得最小值的最优解不唯一,不能出错。
2.探究目标式中的参数范围
【典例4】 已知点O是坐标原点,点A(-1,-2),若点M(x,y)是平面区域上的一个动点,·(-)+≤0恒成立,则实数m的取值范围是________。
【解析】 因为=(-1,-2),=(x,y),所以·(O-)=·=-x-2y。所以不等式·(-)+≤0恒成立等价于-x-2y+≤0,即≤x+2y恒成立。设z=x+2y,作出不等式组表示的可行域如图中阴影部分所示,当目标函数z=x+2y表示的直线经过点D(1,1)时取得最小值,最小值为1+2×1=3;当目标函数z=x+2y表示的直线经过点B(1,2)时取得最大值,最大值为1+2×2=5。所以x+2y∈[3,5],于是要使≤x+2y恒成立,只需≤3,解得m≥或m<0,即实数m
的取值范围是(-∞,0)∪。
【答案】 (-∞,0)∪
【易错总结】 目标函数以向量的形式出现是一种新的创意,本题易错点是面对目标中的向量关系不知道如何转化。求解线性规划问题的基本形式是探究二元目标函数的最值,因此转化向量关系的主要思路和基本目标就是找到其中对应的二元目标函数,然后结合可行域求解最值。
高考中的线性规划问题,既继承了传统的由二元不等式组构成条件,探究二元目标函数最值的基本形式,同时还赋予了创新的命题形式。变更题设条件或目标式中的线性关系为非线性关系,同时渗透参变量的命题风格,增加了可行域条件的动态变化方式,转化了目标函数的探求类型,提升了对问题探究的能力要求,这就要求同学们在面对这些全新的问题时要与时俱进地进行创新分析,增加应变智慧,才能提升我们的解题能力。