人教版高中数学选修2-3练习：第一章章末复习课word版含解析

人教版高中数学选修2-3练习：第一章章末复习课word版含解析

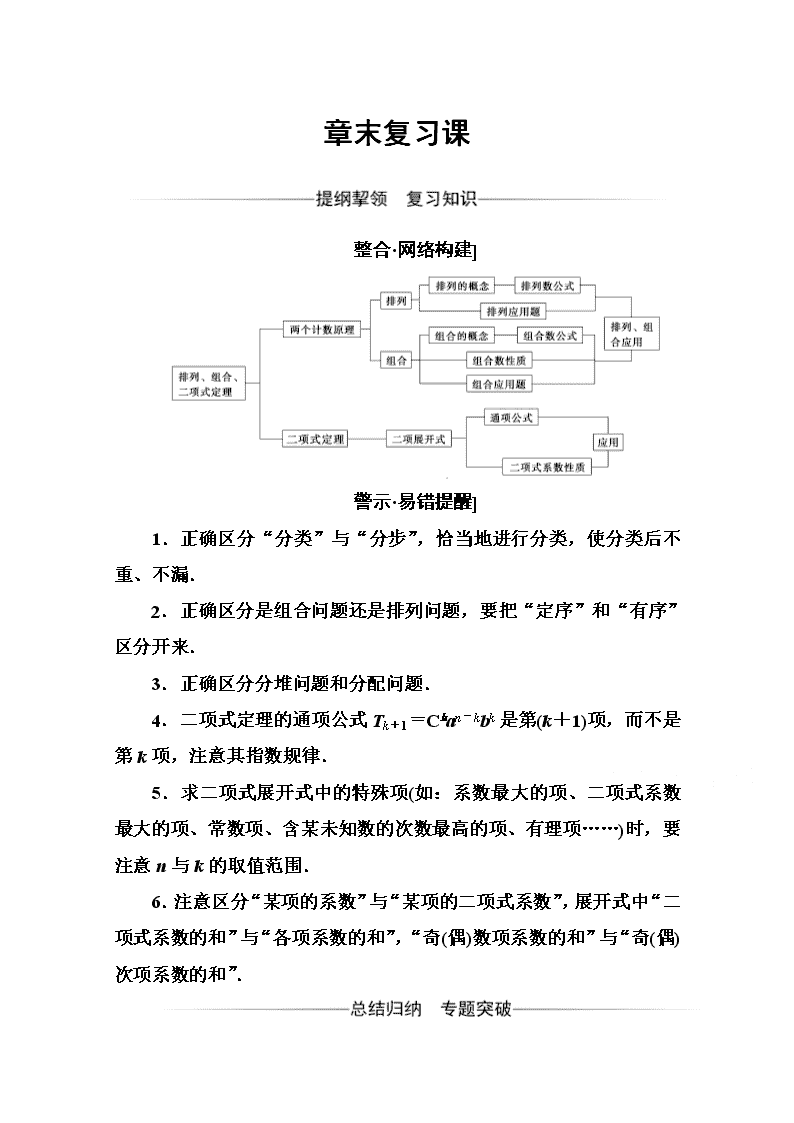
章末复习课 整合·网络构建] 警示·易错提醒] 1．正确区分“分类”与“分步”，恰当地进行分类，使分类后不 重、不漏． 2．正确区分是组合问题还是排列问题，要把“定序”和“有序” 区分开来． 3．正确区分分堆问题和分配问题． 4．二项式定理的通项公式 Tk＋1＝Cknan－kbk是第(k＋1)项，而不是 第 k项，注意其指数规律． 5．求二项式展开式中的特殊项(如：系数最大的项、二项式系数 最大的项、常数项、含某未知数的次数最高的项、有理项……)时，要 注意 n与 k的取值范围． 6．注意区分“某项的系数”与“某项的二项式系数”，展开式中 “二项式系数的和”与“各项系数的和”，“奇(偶)数项系数的和”与 “奇(偶)次项系数的和”． 专题一 两个计数原理的应用 分类加法计数原理和分步乘法计数原理是本章知识的基础，高考 中时有出现，一般是与排列、组合相结合进行考查，难度中等． 例 1] 现有 4种不同颜色要对如图所示的四个部分进行着色，要 求有公共边界的两部分不能用同一种颜色，则不同的着色方法共有 ( ) 高 中 数 学 A.144种 B．72种 C．64种 D．84种 解析：法一 根据所用颜色的种数分类 第一类：用 4种颜色涂，方法有 A44＝4×3×2×1＝24(种)． 第二类：用 3种颜色，必须有一条对角区域涂同色，方法有 C12C14A23 ＝48(种)． 第三类：用 2种颜色，对角区域各涂一色，方法有 A24＝12(种)． 根据加法原理，不同的涂色方法共有 24＋48＋12＝84(种)． 法二 根据“高”“学”是否为同色分类 第一类：区域“高”与“学”同色，从 4色中选 1色，有 C 14种方 法，其余区域“中”“数”各有 3种方法，共有 4×3×3＝36(种)． 第二类：区域“高”与“学”不同色，区域“高”有 4种方法， 区域“学”有 3 种方法，区域“中”“数”各有 2 种方法，共有 4×3×2×2＝48(种)． 根据加法原理，方法共有 36＋48＝84(种)． 答案：D 归纳升华 应用两个原理解决有关计数问题的关键是区分事件是分类完成还 是分步完成，而分类与分步的区别又在于任取其中某一方法是否能完 成该事件，能完成便是分类，否则便是分步．对于有些较复杂问题可 能既要分类又要分步，此时应注意层次清晰，不重不漏，在分步时， 要注意上一步的方法确定后对下一步有无影响(即是否是独立的)． 变式训练] 在∠AOB的 OA边上取 3个点，在 OB边上取 4个点 (均除 O点外)，连同 O点共 8个点，现任取其中三个点为顶点作三角 形，可作的三角形有( ) A．48 B．42 C．36 D．32 解析：分三类：第一类：从 OA边上(不包括 O)任取一点与从 OB 边上(不包括 O)任取两点，可构造一个三角形，有 C13C 24个； 第二类：从 OA边上(不包括 O)任取两点与 OB边上(不包括 O)任 取一点，可构造一个三角形，有 C23C 14个； 第三类：从 OA边上(不包括 O)任取一点与 OB边上(不包括 O)任 取一点，与 O点可构造一个三角形，有 C13C 14个． 由分类加法计数原理，可作的三角形共有 N＝C13C24＋C23C14＋C13C14 ＝42(个)． 答案：B 专题二 排列组合应用题 排列组合应用题是高考的一个重点内容，常与实际问题相结合进 行考查．要认真阅读题干，明确问题本质，利用排列组合的相关公式 与方法解题． 1．合理分类，准确分步． 例 2] 5 名乒乓球队员中，有 2名老队员和 3 名新队员．现从中 选出 3名队员排成 1，2，3号参加团体比赛，则入选的 3名队员中至 少有 1名老队员且 1、2号中至少有 1名新队员的排法有________种(用 数字作答)． 解析：①只有 1名老队员的排法有 C12C23A33＝36(种)．②有 2名老 队员的排法有 C22C13C12A22＝12(种)．所以共有 36＋12＝48(种)． 答案：48 2．特殊优先，一般在后． 例 3] 将 A，B，C，D，E，F六个字母排成一排，且 A，B均 在 C的同侧，则不同的排法共有________种(用数字作答)． 解析：①当 C在第一或第六位时，排法有 A55＝120(种)； ②当 C在第二或第五位时，排法有 A24A33＝72(种)； ③当 C在第三或第四位时，排法有 A22A33＋A23A33＝48(种)． 所以排法共有 2×(120＋72＋48)＝480(种)． 答案：480 3．直接间接，灵活选择． 例 4] 10件产品中有 2件合格品，8件优质品，从中任意取 4件， 至少有 1件是合格品的抽法有________种． 解析：法一 抽取的 4件产品至少有 1件合格品分为有 1件合格 品、2件合格品 2种情况：有 1件合格品的抽法有 C12C 38种；有 2件合 格品抽法有 C22C 28种．根据分类加法计数原理至少有 1件合格品的抽法 共有 C12C38＋C22C28＝140(种)． 法二 从 10件产品中任意抽取 4件，有 C 410种抽法，其中没有合 格品的抽法有 C 48种，因此至少有 1件合格品的抽法有 C410－C48＝210 －70＝140(种)． 答案：140 4．元素相邻，捆绑为一． 例 5] 用数字 1，2，3，4，5组成没有重复数字的五位数，则其 中数字 2，3相邻的偶数有________个(用数字作答)． 解析：数字 2和 3相邻的偶数有两种情况．第一种情况，当数字 2 在个位上时，则 3必定在十位上，此时这样的五位数共有 6个；第二 种情况，当数字 4在个位上时，且 2，3必须相邻，此时满足要求的五 位数有 A22A33＝12(个)，则一共有 6＋12＝18(个)． 答案：18 5．元素相间，插空解决． 例 6] 一条长椅上有 7 个座位，4 个人坐，要求 3个空位中，恰 有 2个空位相邻，共有________种不同的坐法． 解析：先让 4人坐在 4个位置上，有 A 44种排法，再让 2个元素(一 个是两个空位作为一个整体，另一个是单独的空位)插入 4个人形成的 5个“空挡”之间，有 A 25种插法，所以所求的坐法数为 A44A25＝480. 答案：480 6．分组问题，消除顺序． 例 7] 某校高二年级共有六个班级，现从外地转入 4名学生，要 安排到该年级的两个班级且每班安排 2名，则不同的安排方案种数为 ________． 解析：把新转来的 4名学生平均分两组，每组 2人，分法有 C24 A22 ＝ 3(种)，把这两组人安排到 6个班中的某 2个班中去，有 A 26种方法，故 不同的安排种数为 3A26＝90. 答案：90 归纳升华 解排列组合应用题应遵循三大原则，掌握基本类型，突出转化思 想． (1)三大原则是：先特殊后一般的原则、先取后排的原则、先分类 后分步的原则． (2)基本类型主要包括：排列中的“在与不在”问题，组合中的“有 与没有”问题、“相邻与不相邻”问题、“分组问题”等． (3)转化思想：就是把一些排列组合问题与基本类型相联系，从而 把这些问题转化为基本类型，然后加以解决． 专题三 二项式定理的应用 二项式定理是历年高考中的必考内容，解决二项式定理问题，特 别是涉及求二项展开式的通项的问题，关键在于抓住通项公式，还要 注意区分“二项式系数”与“展开式系数”． 例 8] (1)已知 x2－ i x n 的展开式中第三项与第五项的系数之比为 － 3 14 ，其中 i2＝－1，则展开式中系数为实数且最大的项为( ) A．第三项 B．第四项 C．第五项 D．第五项或第六项 (2)设(3x－1)6＝a6x6＋a5x5＋a4x4＋a3x3＋a2x2＋a1x＋a0，则 a6＋a4 ＋a2＋a0＝________． 解析：(1)T3＝－C2nx2n－5，T5＝C4nx2n－10. 由－ C2n C4n ＝－ 3 14 ，得 n2－5n－50＝0，解得 n＝10(舍去 n＝－5)， 又 Tr＋1＝Cr10(－i)rx20－ 5 2 r， 据此可知当 r分别取 0，2，4，6，8，10时其系数为实数，且当 r ＝4时，C410＝210为最大． (2)令 x＝1，得 a6＋a5＋a4＋a3＋a2＋a1＋a0＝26＝64； 令 x＝－1，得 a6－a5＋a4－a3＋a2－a1＋a0＝4 096. 两式相加，得 2(a6＋a4＋a2＋a0)＝4 160， 所以 a6＋a4＋a2＋a0＝2 080. 答案：(1)C (2)2 080 归纳升华 (1)区分“项的系数”与“二项式系数”．项的系数与 a，b有关， 可正可负，二项式系数只与 n有关，恒为正数． (2)切实理解“常数项”“有理项(字母指数为整数)”“系数最大 的项”等概念． (3)求展开式中的指定项，要把该项完整写出，不能仅仅说明是第 几项． (4)赋值法求展开式中的系数和或部分系数和，常赋的值为 0，±1 等． 变式训练] (1) x－ 2 x3 5 展开式中的含 x－3的项的系数为( ) A．80 B．60 C．40 D．－40 (2)已知(1＋x)6(1－2x)5＝a0＋a1x＋a2x2＋…＋a11x11，则 a1＋a2＋… ＋a11＝________． 解析：(1)设展开式的第(r＋1)项为 Tr＋1＝Cr5x5－r － 2 x3 r ＝(－2)rCr5x5 －4r，令 5－4r＝－3，得 r＝2， 所以，展开式中含 x －3的项为 T3＝(－2)2C25x－3＝40x－3. (2)令 x＝0，得 a0＝1；令 x＝1，得 a0＋a1＋a2＋…＋a11＝－64. 所以 a1＋a2＋…＋a11＝－65. 答案：(1)C (2)－65 专题四 分类讨论思想 分类讨论思想在解决排列组合问题时经常应用，此类问题一般情 况繁多，因此要对各种不同的情况进行合理的分类与准确的分步，以 便有条不紊地进行解答，避免重复或遗漏的现象发生． 例 4] 从 10种不同的作物中选出 6种放入 6个不同的瓶子中展 出，如果甲、乙两种种子不能放入第 1号瓶内，那么不同的放法共有 ________种． 解析：根据选出的 6种种子中所含甲、乙种子个数来分类：选出 的 6种种子中只含甲或只含乙的不同放法都为 C58A15A55；选出的 6种种 子中，同时含有甲与乙的不同放法有 C48A25A44；选出的 6种种子中，都 不含甲与乙的不同放法有 A68.故不同的放法共有 2C58A15A55＋C48A25A44＋ A68＝120 960(种)． 答案：120 960 归纳升华 排列组合的综合问题一般比较复杂，分类方法也灵活多变．一般 有以下一些分类方式：(1)根据元素分类，又包括根据特殊元素分类， 根据元素特征分类，根据特殊元素的个数分类；(2)根据特殊位置分类； (3)根据图形分类，又包括根据图形的特征分类，根据图形的种类分类； (4)根据题设条件分类． 变式训练] 由 1，2，3，4，5，6六个数字可组成________个无 重复且是 6的倍数的五位数． 解析：若一个整数是偶数且是 3的倍数，则这个整数是 6的倍数．据 此本题分两类求解． 第一类：由 1，2，4，5，6作数码．首先从 2，4，6中任选一个 作为个位数字，有 A 13种选法，然后其余四个数字在其他数位上全排列， 有 A 44种选法，所以符合条件的五位数共有 N1＝A13A44＝72(个)． 第二类：由 1，2，3，4，5作数码．依照第一类的方法，符合条 件的五位数有 N2＝A12A44＝48(个)． 综上，符合条件的五位数共有 N＝N1＋N2＝120(个)． 答案：120