北师版高中数学必修一第12讲：幂函数（学生版）

北师版高中数学必修一第12讲：幂函数（学生版）

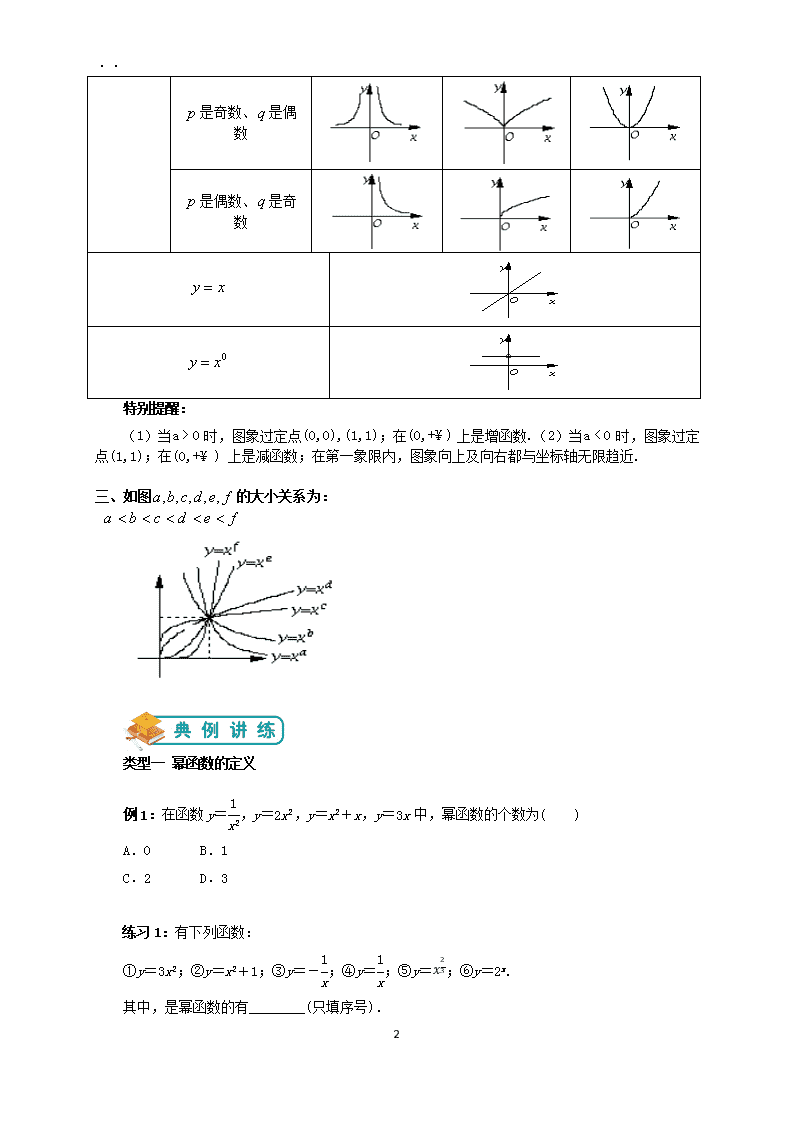
·· 1 幂函数 __________________________________________________________________________________ __________________________________________________________________________________ 1、通过实例，了解幂函数的概念；结合函数y = x ，y = ， y = ， y = ，的图像，了解 它们的变化情况. 2、通过对幂函数的研究，加深对函数概念的理解. 一、定义： 一般地，我们把形如  ay x a R  的函数叫做幂函数，其中 a 为常数。 特别提醒： 幂函数的基本形式是 y = ，其中x是自变量，a 是常数. 要求掌握 y = x ，y = ， y = ， y = ， y = 这五个常用幂函数的图象. 二、幂函数性质： 1、所有的幂函数在 0, 都有定义，并且图像都通过点 1,1 ； 2、如果 0a  ，则幂函数的图像经过原点，并且在区间 0, 上为增函数；如果 0a  ，则幂 函数的图像不经过原点，并且在区间 0, 上为增函数 3、幂函数的图像及其奇偶性： 令 a q p  （ p 、 q 互质） a  0 0  a  1 a  1 q py x （ p 、q 互 质） p 、 q 是奇数 ·· 2 p 是奇数、q 是偶数 p 是偶数、q 是奇数 y x 0y x 特别提醒： （1）当a > 0 时，图象过定点(0,0),(1,1)；在(0,+¥ ) 上是增函数.（2）当a < 0 时，图象 过定点(1,1)；在(0,+¥ ) 上是减函数；在第一象限内，图象向上及向右都与坐标轴无限趋近. 三、如图 , , , , ,a b c d e f 的大小关系为： a b c d e f     类型一 幂函数的定义 例 1：在函数 y＝1 x2，y＝2x2，y＝x2＋x，y＝3x 中，幂函数的个数为( ) A．0 B．1 C．2 D．3 练习 1：有下列函数： ①y＝3x2；②y＝x2＋1；③y＝－1 x ；④y＝1 x ；⑤y＝ ；⑥y＝2x. 其中，是幂函数的有________(只填序号)． ·· 3 练习 2：函数 y＝(k2－k－5)x2 是幂函数，则实数 k 的值是( ) A．k＝3 B．k＝－2 C．k＝3 或 k＝－2 D．k≠3 且 k≠－2 类型二 幂函数的图象和性质 例 2：幂函数 y＝xm，y＝xn，y＝xp，y＝xq 的图象如图，则将 m、n、p、q 的大小关系用“<”连 接起来结果是________． 练习 1：(2014～2015 学年度江西鹰潭一中高一上学期月考)已知幂函数 f(x)＝kxα的图象过点 1 2 ， 2 ，则 k－α＝( ) A．1 2 B．1 C．3 2 D．2 练习 2：(2014～2015 学年度安徽宿州市十三校高一上学期期中测试)已知幂函数 y＝(m2－5m－ 5)x2m＋1 在(0，＋∞)上单调递减，则实数 m＝( ) A．1 B．－1 C．6 D．－1 或 6 类型三 函数值大小的比较 例 3：比较下列各组数的大小 练习 1：下列关系中正确的是( ) A．(1 2) 2 3 <(1 5) 2 3 <(1 2) 1 3 B．(1 2) 2 3 <(1 2) 1 3 <(1 5) 2 3 C．(1 5) 2 3 <(1 2) 1 3 <(1 2) 2 3 D．(1 5) 2 3 <(1 2) 2 3 <(1 2) 1 3 ·· 4 练习 2：比较下列三个值的大小 ， 4 ， ； 1、如图曲线是幂函数 y＝xn 在第一象限内的图象，已知 n 取±2，±1 2 四个值，相应于曲线 C1、C2、 C3、C4 的 n 依次为( ) A．－2，－1 2 ，1 2 ，2 B．2，1 2 ，－1 2 ，－2 C．－1 2 ，－2,2，1 2 D．2，1 2 ，－2，－1 2 2、下列命题中正确的是( ) A．幂函数的图象不经过点(－1,1) B．幂函数的图象都经过点(0,0)和点(1,1) C．若幂函数 f(x)＝xa 是奇函数，则 f(x)是定义域上的增函数 D．幂函数的图象不可能出现在第四象限 3、函数 y＝|x|1 2 的图象大致为( ) 4、设函数 y＝ax－2－1 2(a>0，且 a≠1)的图象恒过定点 A，若点 A 在幂函数 y＝xα的图象上，则该 幂函数的单调递减区间是( ) A．(－∞，0) B．(0，＋∞) C．(－∞，0)，(0，＋∞) D．(－∞，＋∞) 5、若函数 f(x)＝(2m＋3)xm2－3 是幂函数，则 m 的值为________． 6、(2014～2015 学年度浙江舟山中学高一上学期期中测试)已知幂函数 y＝f(x)的图象过点(2,8)， 则 f(x)＝______________. ·· 5 _________________________________________________________________________________ _________________________________________________________________________________ 基础巩固 1．如图所示为幂函数 y＝xm 与 y＝xn 在第一象限内的图象，则( ) A．－1＜n＜0＜m＜1 B．n＜0＜m＜1 C．－1＜n＜0，m＜1 D．n＜－1，m＞1 2．函数 y＝x3 与函数 y＝x 1 3 的图象( ) A．关于原点对称 B．关于 x 轴对称 C．关于 y 轴对称 D．关于直线 y＝x 对称 3．某工厂第三年的产量比第一年的产量增长 44%，若每年的平均增长率相同(设为 x)，则下列 结论中正确的是( ) A．x>22% B．x<22% C．x＝22% D．x 的大小由第一年产量确定 4．某种细菌在培养过程中，每 15 min 分裂一次(由 1 个分裂成 2 个)，则这种细菌由 1 个繁殖成 212 个需经过( ) A．12 h B．4 h C．3 h D．2 h 5．某山区为加强环境保护，绿色植被的面积每年都比上一年增长 10.4%，那么，经过 x 年，绿 色植被面积可以增长为原来的 y 倍，则函数 y＝f(x)的图象大致为( ) ·· 6 能力提升 6．若幂函数 y＝(m2－3m＋3)xm2－m－2 的图象不过原点，则 m 是__________． 7．如果幂函数 y＝xa 的图象，当 0

查看更多