数学人教B版必修4教案：3-1-1 两角和与差的余弦公式2 Word版含答案

数学人教B版必修4教案：3-1-1 两角和与差的余弦公式2 Word版含答案

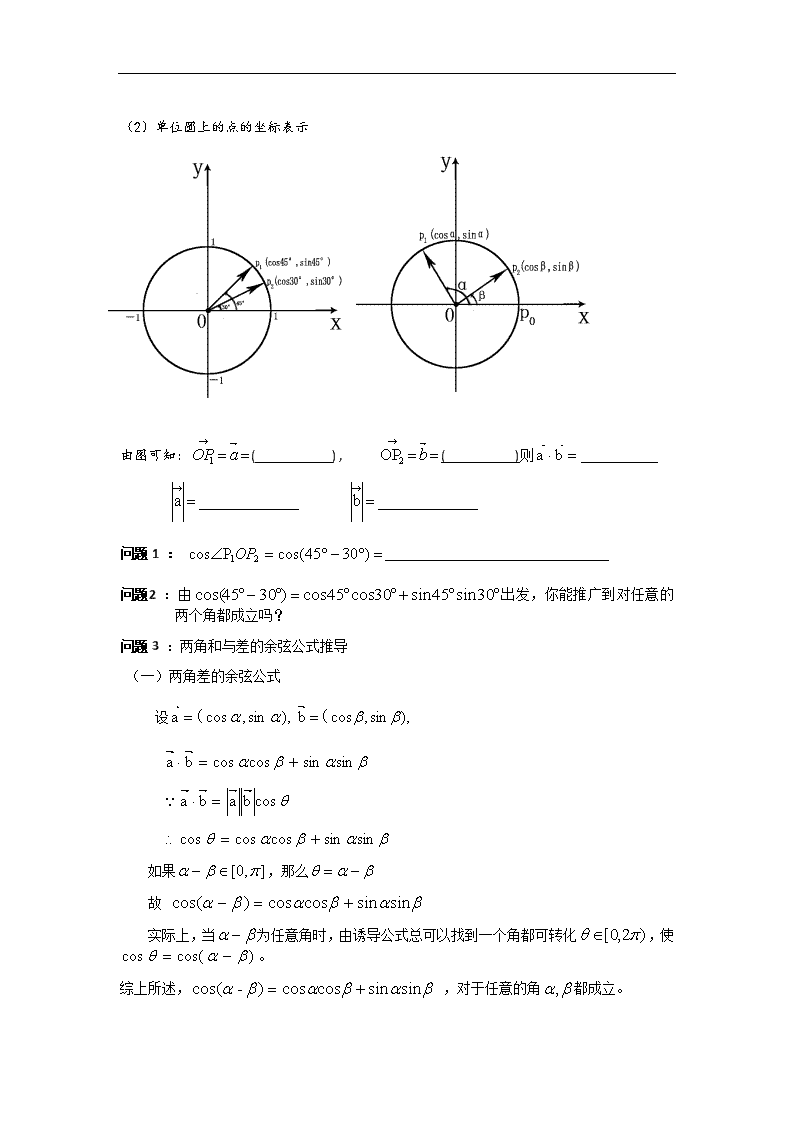
两角和与差的余弦公式教学设计 【教学三维目标】 1.知识与技能目标： 理解两角和与差的余弦公式的推导过程，熟记两角和与差的余弦公式， 运用两角和与差的余弦公式，解决相关数学问题；培养学生严密而准确的数学表达能力；培 养学生逆向思维和发散思维能力； 2 过程与方法目标 ：通过对公式的推导提高学生研究问题、分析问题、解决问题能力；体 会公式探求中从特殊到一般的数学思想，同时渗透如上所说的多种数学思想。 3.情感、态度、价值观目标： 通过观察、对比体会数学的对称美和谐美，培养学生良好的 数学表达和思考的能力，学会从已有知识出发主动探索未知世界的意识及对待新知识的良好 情感态度。 【高考等级要求】 C 级 【教学重点】 两角和与差的余弦公式的理解与灵活运用。 【教学难点】 两角和与差的余弦公式的推导过程，特别是一般性的推广。 【突破措施】 先由特殊情形引入再向一般性过渡，充分挖掘学生的思考和探究能力，以达 到对公式的深入理解和灵活运用。 【教材分析】 这节内容是教材必修 4 的第三章《三角恒等变换》第一节，是高考的重点考 点，历年高考必考内容，一般在填空或解答题第 15 题出现。教材在学生掌握了任意角的三 角函数的概念、向量的坐标表示以及向量数量积的坐标表示的基础上，进一步研究用单角的 三角函数表示的两角和与差的三角函数．“两角差的余弦公式”在教科书中采用了一种易于 教学的推导方法，即先借助于单位圆中的三角函数线，推出α，β，α－β均为锐角时成立．对 于α，β为任意角的情况，教材运用向量的知识进行了探究．同时，补充了用向量的方法推 导过程中的不严谨之处，这样，两角差的余弦公式便具有了一般性。 【学情分析】 本课时面对的学生是高一年级的学生，数学表达能力和逻辑推理能力正处于 高度发展的时期，学生对探索未知世界有主动意识，对新知识充满探求的渴望。他们经过半 个多学期的高中生活，储备了一定的数学知识，掌握了一些高中数学的学习方法，这为本节 课的学习建立了良好的知识基础。 【学具准备】 小黑板 圆规 【学法设计】 独立思考，生生交流探究，小组合作 【知识链接】 诱导公式 平面向量的数量积 一、 产生对公式的需求 引入新课 （1 分钟） 首先让学生通过具体实例消除对“cos(α-β)=cosα-cosβ”的误解，说明两角和（差） 的三角函数不能按分配律展开。并鼓励同学对公式结构的可能情况进行大胆猜想和尝试性探 索。 二、自主探究 引发思考 层层深入 得出结论 （8 分钟） 独立思考以下问题： (1)向量的数量积 __________ba  ),,a 11 yx（ ),b 22 yx（ 则 __________ba  （2）单位圆上的点的坐标表示 由图可知：   aOP1 ( ) ,   b2OP ( )则  ba _____________a   _____________b   问题 1 ：  )3045cos(Pcos 21OP 问题2 ：由  30sin45sin30cos45cos)3045cos( 出发，你能推广到对任意的 两个角都成立吗？ 问题 3 ：两角和与差的余弦公式推导 （一）两角差的余弦公式 设 ),sin,cosa （ ),sin,cosb （  sinsincoscosba  cosbaba   sinsincoscoscos  如果 ],0[   ，那么   故  sinsincoscos)cos(  实际上，当   为任意角时，由诱导公式总可以找到一个角都可转化 )2,0[   ，使 )cos(cos   。 综上所述，  sinsincoscos)-cos(  ，对于任意的角 , 都成立。 根据两角差的余弦公式，你可以猜猜 ?)cos(   提示：令   （二）两角和的余弦公式（学生回答）  sinsincoscos)cos(  结论： ）（两角和与差的余弦公式  C  )cos(   sinsincoscos  注： 1.公式中两边的符号正好相反（一正一负）； 2.式子右边同名三角函数相乘再加减，且余弦在前正弦在后； 3.式子中α、β是任意的。 4 式子的逆用，变形用 正因为α、β的任意性，所以赋予 C(α+β)公式的强大生命力 三． 互相交流，小组活动 公式应用闯关 （12 分钟） 第一关：小试身手 请用特殊角分别代替公式中α、β，你能求哪些非特殊角的值呢？（选择的特殊角可以 是 30°60°45°等） (1) 0cos15 ______ ；(2) 0cos75 ______ ；(3) 0cos105 ______ ；…… 问题预测：学生动笔自由尝试、主动探索。有的同学说会求 cos15°、cos75°、cos105°、 cos(-15°)、cos165°……的值。甚至可能有的同学会说他验证了 cos30°=sin60°……. （让同学感受获得公式后的第一份喜悦）由于初学公式的应用，我选择其中之一作示范。 第二关：再接再厉 若β固定，分别用 2 π,π 代替α，你将会发现什么结论呢？ (1)cos( ) ___________(2)cos( ) ___________ (3)cos( ) __________(4)cos( ) ___________2 2                设计意图：引导同学发现余弦的诱导公式可用 C(α±β)公式得到证明： .sin)2cos(,sin)2cos(,cos)cos(   初步让学生发现 C(α±β) 公式是诱导公式的推广。（从而让同学感受获得公式后的第二份喜悦） 第三关：各显神通 倘若让你对 C(α±β)公式中的α、β自由赋值，你又将发现什么结论呢？ (1)cos __________4   （ ） ；(2)cos ____________  （ ） (3)   ____)____)sin(______sin(_cos(_____)(_____)coscos   ）（ (4)   ___)___)sin(______sin(__cos(_____)cos(_____)cos  ）（）（  …… 问题预测：可能有的同学发现 cos2α=cos(α+α)=cos2α-sin2α，这是以后要学的二 倍角公式，还有的同学发现： cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ，甚 至有调皮的同学发现 cos0=cos(α-α)=cos2α+sin2α=1，这就无意中证明了平方关 系，……， （据此，让同学感受到 C(α±β)公式的强大功能）。（必要时，教师可适当提示）。 注：按课本编排未必能让同学注意公式中α,β的任意性，（而正是因α、β的任意性， 所以才赋予 C(α+β)公式的强大生命力）。于是我设计上述三个有层次的 A ,B,C 级的问题，留 时间先让同学用特殊角自由赋值，逐渐摸索、尝试，不断总结、归纳。这样更能使同学亲自 感受公式的强大功能，并掌握赋值法。 四．师生共同活动 数学运用 （10 分钟） 1.例题：知 )2 3,(,5 3cos),,2(,3 2sin   ，求 )cos(   的值。 解：由 ),2(   ，得 3 5 3 211cos 2 2sin       又由 )2 3,(   ，得 5 4 5 311sin 2 2cos       由余弦的和角公式得  sinsincoscos)cos(  5 3 2 4 8 3 5( )( )3 5 3 5 15          注意：注意角 、  的象限，也就是符号问题. 2.变式练习 能力提高 的值。求都是锐角，已知  cos,13 5)cos(,5 4cos,  解：由 )20(  ， ，得 5 3 5 411sin 2 2cos       又由 )2,0(   ，则 ),0(   得 13 12 13 51)(1)sin( 2 2cos       由余弦得差角公式得    sinsincoscoscoscos ）（）（）（  5 4 12 3 16( )( )13 5 13 5 65       五．达标检测： （10 分钟） （1）cos80°cos20°+sin80°sin20°，初步学会逆用公式。 （2）cos130°cos5°-sin130°sin5° （3） cos215°-sin215°， 为二倍角公式埋下伏笔。 （4） cos80°cos35°+cos10°cos55°，逐步学会把不符合公式结构变形使之 符合。 （5） （ 2004 全 国 高 考 题 ） 设 0, 2      ， 若 3cos 5   ， 则 2 cos _____4      ，利用高考题的引用让学生串连三角函数的相关知 识。 ⑴. 2 1 ⑵. - 2 2 ⑶. 2 3 ⑷. 2 2 ⑸. 5 1 六．学习反思 （2 分钟） 知识网建构： 七． 课堂总结: （2 分钟） 1、牢记公式的结构特点，学会逆用公式。不符合公式结构特点的，常通过诱导公式变 形使之符合。 2、强调公式中α、β的任意性，是本节内容的主线，它赋予了公式的强大生命力。 注：逆用公式是学生认识和掌握公式的重要标志。通过步步加深的练习，加强学生对公 平面内两点间的距离公式 C (α+β) C (α-β) 以-β代β 求 cos15°等 赋值 诱导公式及其它 α、β任意角 式的理解和应用，引导学生积极参与思维，培养学生观察，比较等思维能力，同时渗透了一 种化归思想。 八． 作业布置 1. 教材第 94 页，感受理解第 1，2. 3 题 2. 探究：知道了 )cos(   ，你觉得 )sin(   也有类似的规律吗？ 九． 板书设计 课题：3.1.1 两角和与差的 余弦 两角差的余弦公式 c o s ( ) c o s c o s s in s in          两角和的余弦公式 c o s ( ) c o s c o s s in s in          例题 变式练习 十．【教学反思】 两角差的余弦公式是任意角三角函数知识的延伸，是后继内容两角和与差的正弦、余 弦、正切，以及二倍角公式的知识基础。 之前我在新旧教材中都讲过这个内容，经过这次 培训，我又对这一内容进行了设计，重新备课。就之前与之后的教学，我进行了反思。 一、 反思教学理念：新课程理念的灵魂是三个教学目标的整合，关注学生的发展。知识可 以通过传授获得，技能可以通过训练掌握。态度和情感价值观需要学生参与获得。这样，课 堂教学中，要重视学生的参与、体验过程。但老师的指导作用也不可忽视，没有老师的引导， 学生的行动、思维就很难达到一个较高的程度。教师通过创设激发学生学习欲望的数学情境， 营造积极的活跃的学习氛围，才能使学生参与我们的教学中来。 二、反思教学过程： （一）创设问题情境：之前旧教材的教学，我们只关注公式的应用，而轻视公式的由来，这 样符合公式的发生发展过程。这次的教学设计我从如何解决一个实际问题出发，调动学生的 思维与学习积极性，抓住学生的兴趣。 （二）两角差的余弦公式的探究过程：之前旧教材的教学是用两点间的距离公式来推导两角 和的余弦，再赋值得到两角差的余弦公式，这一过程中对学生的思维训练不是很多。而新教 材采用了一种学生易于接受的推导方法，即先用数形结合的思想，借助于单位圆中的三角函 数线，推出α，β，α－β均为锐角时公式成立。对于α，β为任意角时的情况，教材运用 向量的知识进行了探究，使得公式的得出成为一个纯粹的代数运算过程，学生易于理解和掌 握，同时也有利于提高学生运用向量解决相关问题的意识和能力。我采用了新教材的思路。 (三)两角差的余弦公式的简单应用。除了课本上的例题、习题，我补充了课堂练习、及课 后作业，针对性较强。