2020-2021学年数学新教材人教A版选择性必修第一册教案:第1章 1
www.ks5u.com
1.4.2 用空量研究距离、夹角问题
学 习 目 标
核 心 素 养
1.会用向量法求线线、线面、面面的夹角以及距离问题.(重点、难点)
2.正确区分向量夹角与所求线线角、面面角的关系.(易错点)
通过利用空间向量求异面直线所成的角、直线与平面所成的角、二面角和距离的学习,提升学生的逻辑推理、数学运算的核心素养.
(1)已知a,b为非零向量,它们的夹角为θ,那么cos θ=cos〈a,b〉=.
(2)空间中有三种角:异面直线所成的角,直线与平面所成的角和两个平面的夹角.
(3)空间中的三种基本距离:点点距、点线距和点面距.利用直线的方向向量和平面的法向量可以判断线线、线面和面面的平行、垂直问题,能否利用它们求出三种空间角和空间距离呢?
1.空间角的向量求法
角的分类
向量求法
范围
两异面直线l1与l2所成的角为θ
设l1与l2的方向向量分别为u,v,则cosθ=|cos
|=
直线l与平面α所成的角为θ
设l的方向向量为u,平面α的法向量为n,则sin θ=|cos|=
平面α与平面β的夹角为θ
设平面α,β的法向量分别为n1,n2,则cos θ=|cos|=
思考:直线与平面所成的角和直线的方向向量与平面的法向量所成的角有怎样的关系?
[提示] 设n为平面α的一个法向量,a为直线a的方向向量,直线a与平面α所成的角为θ,则
θ=
2.空间距离的向量求法
分类
向量求法
两点距
设A、B为空间中的任意两点,则d=|AB|
点线距
设直线l的单位方向向量为u,A∈l,P∉l,设=a,则点P到直线l的距离d=
点面距
已知平面α的法向量为n,A∈α,P∉α,则点P到平面α的距离为d=
1.思考辨析(正确的打“√”,错误的打“×”)
(1)两异面直线所成的角与两直线的方向向量所成的角相等. ( )
(2)直线l与平面α的法向量的夹角的余角就是直线l与平面α所成的角. ( )
(3)平面α和β的夹角为θ,平面α,β的法向量分别为n1,n2,则θ=〈n1,n2〉. ( )
[提示] (1)× (2)× (3)×
2.已知向量m,n分别是直线l与平面α的方向向量、法向量,若cos〈m,n〉=-,则l与α所成的角为( )
A.30° B.60° C.150° D.120°
B [设l与α所成的角为θ,则sin θ=|cos〈m,n〉|=,又0°≤θ≤90°,∴θ=60°,应选B.]
3.两平行平面α,β分别经过点O(0,0,0)和点A(2,1,1),且两平面的一个法向量n=(-1,0,1),则两平面间的距离是________.
[两平行平面α,β分别经过坐标原点O和点A(2,1,1),
=(2,1,1),且两平面的一个法向量n=(-1,0,1),∴两平面间的距离d==.]
4.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面的夹角的大小为________.
45° [cos θ===,由于θ∈,∴θ=45°.]
距离问题
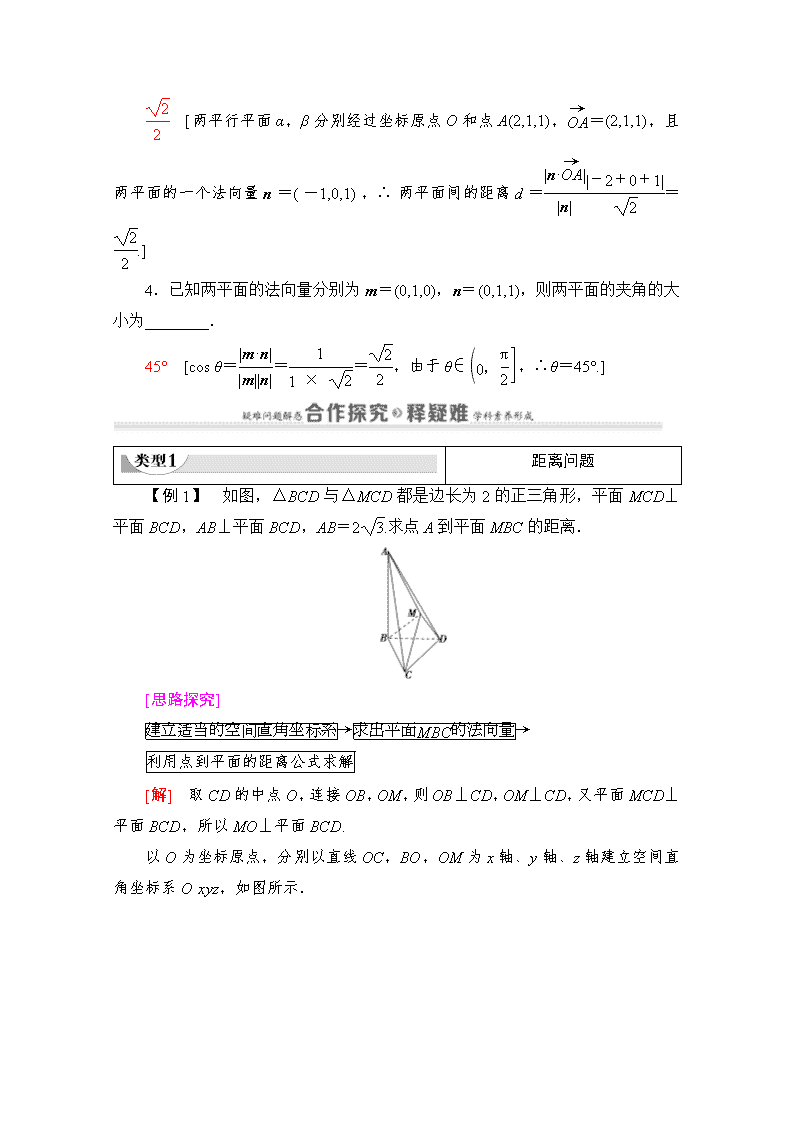
【例1】 如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2.求点A到平面MBC的距离.
[思路探究]
→→
利用点到平面的距离公式求解
[解] 取CD的中点O,连接OB,OM,则OB⊥CD,OM⊥CD,又平面MCD⊥平面BCD,所以MO⊥平面BCD.
以O为坐标原点,分别以直线OC,BO,OM为x轴、y轴、z轴建立空间直角坐标系Oxyz,如图所示.
因为△BCD与△MCD都是边长为2的正三角形,所以OB=OM=,则O(0,0,0),C(1,0,0),M(0,0,),B(0,-,0),A(0,-,2),所以=(1,,0),=(0,,),=(0,0,2).
设平面MBC的法向量为n=(x,y,z),
由得
即取x=,可得平面MBC的一个法向量为n=(,-1,1).
又=(0,0,2),所以所求距离d==.
求点到平面的距离的四步骤
[跟进训练]
1.在长方体OABCO1A1B1C1中,OA=2,AB=3,AA1=2,求O1到直线AC的距离.
[解] 法一:建立如图所示的空间直角坐标系,则A(2,0,0),O1(0,0,2),
C(0,3,0),过O1作O1D⊥AC于点D,设D(x,y,0),=(x-2,y,0),=(x,y,-2),
∵=(-2,3,0),⊥,
∥,∴
解得∴D,
∴||==.
即O1到直线AC的距离为.
法二:建立如图所示的空间直角坐标系.
则A(2,0,0),O1(0,0,2),C(0,3,0),
∴=(-2,0,2),
=(-2,3,0),
∴·=(-2,0,2)·(-2,3,0)=4,
∴在方向上的投影为
=,∴O1到直线AC的距离
d==.
求两条异面直线所成的角
【例2】 如图,在三棱柱OABO1A1B1中,平面OBB1O1⊥平面OAB,∠O1OB=60°,∠AOB=90°,且OB=OO1=2,OA=,求异面直线A1B与AO1所成角的余弦值的大小.
[思路探究] 建立空间直角坐标系→用坐标表示向量和→运用向量法求A1B与AO1的夹角
[解] 建立如图所示的空间直角坐标系,则O(0,0,0),O1(0,1,),A(,0,0),A1(,1,),B(0,2,0),
∴=(-,1,-),
=(,-1,-).
∴|cos〈,〉|=
==.
∴异面直线A1B与AO1所成角的余弦值为.
用坐标法求异面直线所成角的一般步骤
(1)建立空间直角坐标系;
(2)分别求出两条异面直线的方向向量的坐标;
(3)利用向量的夹角公式计算两条直线的方向向量的夹角;
(4)结合异面直线所成角的范围求出异面直线所成的角.
[跟进训练]
2.如图,在三棱锥VABC中,顶点C在空间直角坐标系的原点处,顶点A,B,V分别在x,y,z轴上,D是线段AB的中点,且AC=BC=2,∠VDC=,求异面直线AC与VD所成角的余弦值.
[解] 因为AC=BC=2,D是AB的中点,所以C(0,0,0),A(2,0,0),B(0,2,0),D(1,1,0).
在Rt△VCD中,CD=,∠VDC=,故V(0,0,).
所以=(-2,0,0),=(1,1,-).
所以cos〈,〉===-.
所以异面直线AC与VD所成角的余弦值为.
直线与平面所成的角
【例3】 如图,已知三棱柱ABCA1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.
(1)证明:EF⊥BC;
(2)求直线EF与平面A1BC所成角的余弦值.
[思路探究] 连接A1E,先证明A1E⊥面ABC,再以E为原点建立空间直角坐标系,写出相关点及向量的坐标,利用向量的坐标运算证明EF⊥BC,再利用向量法求直线与平面所成角的余弦值.
[证明] (1)连接A1E,因为A1A=A1C,E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC,A1E⊂平面A1ACC1,
平面A1ACC1∩平面ABC=AC,所以,A1E⊥平面ABC.
如图,以点E为原点,分别以射线EC,EA1为y,z轴的正半轴,建立空间直角坐标系Exyz.
不妨设AC=4,则A1(0,0,2),B(,1,0),B1(,3,2),F,C(0,2,0).
因此,=,=(-,1,0).
由·=0得EF⊥BC.
(2)设直线EF与平面A1BC所成角为θ,
由(1)可得=(-,1,0),=(0,2,-2),设平面A1BC的法向量为n=(x,y,z),
由,得,
取n=(1,,1),故sin θ=|cos〈,n〉|==.
因此直线EF与平面A1BC所成角的余弦值为.
求直线与平面的夹角的思路与步骤
思路一:找直线在平面内的射影,充分利用面与面垂直的性质及解三角形知识可求得夹角(或夹角的某一三角函数值).
思路二:用向量法求直线与平面的夹角可利用向量夹角公式或法向量.利用法向量求直线与平面的夹角的基本步骤.
(1)建立空间直角坐标系;
(2)求直线的方向向量;
(3)求平面的法向量n;
(4)计算:设线面角为θ,则sin θ=.
[跟进训练]
3.如图,在正三棱柱ABCA1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.
(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
[解] 如图,在正三棱柱ABCA1B1C1中,设AC,A1C1的中点分别为O,O1,则OB⊥OC,OO1⊥OC,OO1⊥OB,以{,,}为基底,建立空间直角坐标系O
xyz.
因为AB=AA1=2,所以A(0,-1,0),B(,0,0),C(0,1,0),A1(0,-1,2),B1(,0,2),C1(0,1,2).
(1)因为P为A1B1的中点,
所以P,
从而=,=(0,2,2),
故|cos〈,〉|===.
因此,异面直线BP与AC1所成角的余弦值为.
(2)因为Q为BC的中点,所以Q,
因此=,=(0,2,2),=(0,0,2).
设n=(x,y,z)为平面AQC1的一个法向量,
则即
不妨取n=(,-1,1).
设直线CC1与平面AQC1所成的角为θ,
则sin θ=|cos〈,n〉|===,
所以直线CC1与平面AQC1所成角的正弦值为.
平面与平面的夹角
[探究问题]
1.二面角与平面的夹角范围一样吗?
[提示] 不一样.二面角的范围为[0,π],而两个平面的夹角是不大于直角的角,范围是.
2.两平面的夹角与二面角的两个半平面的法向量所成的角有怎样的关系?
[提示] 两平面的法向量分别为u,v,若〈u,v〉为锐角时,两平面的夹角等于〈u,v〉,若〈u,v〉为钝角时,两平面的夹角等于π-〈u,v〉.
【例4】 如图,四棱柱ABCDA1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求平面C1OB1与平面DOB1的夹角的余弦值.
[思路探究] 建立空间直角坐标系,根据∠CBA=60°,建立棱长之间的关系,写出相关点的坐标和向量的坐标,再求两平面的夹角.
[解] (1)证明:因为四边形ACC1A1和四边形BDD1B1均为矩形,所以CC1⊥AC,DD1⊥BD,
又CC1∥DD1∥OO1,所以OO1⊥AC,OO1⊥BD,
因为AC∩BD=O,所以O1O⊥底面ABCD.
(2)因为四棱柱的所有棱长都相等,所以四边形ABCD为菱形,AC⊥BD.又O1O⊥底面ABCD,所以OB,OC,OO1两两垂直.如图,以O为原点,OB,OC,OO1所在直线分别为x,y,z轴,建立空间直角坐标系.
设棱长为2,因为∠CBA=60°,所以OB=,OC=1,
所以O(0,0,0),B1(,0,2),C1(0,1,2),
平面BDD1B1的一个法向量为n=(0,1,0),
设平面OC1B1的法向量为m=(x,y,z),
则由m⊥,m⊥,所以
取z=-,则x=2,y=2,
所以m=(2,2,-),
所以cos〈m,n〉===.
所以平面C1OB1与平面DOB1的夹角的余弦值为.
1.[变设问]本例条件不变,求面BA1C与面DA1C的夹角的余弦值.
[解] 建立如图所示的空间直角坐标系.设棱长为2,则A1(0,-1,2),
B(,0,0),C(0,1,0),
D(-,0,0).
所以=(-,1,0),=(0,2,-2),=(-,-1,0).
设平面A1BC的法向量为n1=(x1,y1,z1),
则即
取x1=,则y1=z1=3,
故n1=(,3,3).
设平面A1CD的法向量为n2=(x2,y2,z2),
则即
取x2=,则y2=z2=-3,
故n2=(,-3,-3).
所以cos〈n1,n2〉==-=-.
所以面BA1C与面DA1C的夹角的余弦值为-.
2.[变条件、变设问]本例四棱柱中,∠CBA=60°改为∠CBA=90°,设E,F分别是棱BC,CD的中点,求平面AB1E与平面AD1F的夹角的余弦值.
[解] 以A为坐标原点建立空间直角坐标系,如图所示,设此棱柱的棱长为1,则A(0,0,0),B1(1,0,1),E,D1(0,1,1),F,=,=(1,0,1),=,=(0,1,1).
设平面AB1E的法向量为n1=(x1,y1,z1),
则即
令y1=2,则x1=-1,z1=1,所以n1=(-1,2,1).
设平面AD1F的法向量为n2=(x2,y2,z2).
则
即
令x2=2,则y2=-1,z2=1.
所以n2=(2,-1,1).
所以平面AB1E与平面AD1F的夹角的余弦值为==.
利用向量法求两平面夹角的步骤
(1)建立空间直角坐标系;
(2)分别求出二面角的两个半平面所在平面的法向量;
(3)求两个法向量的夹角;
(4)法向量夹角或其补角就是两平面的夹角(不大于90°的角).
1.向量法求空间角的一般步骤
(1)向量表示
法一:选不共面的三个向量为基底,进行基底表示;法二:建立适当的坐标系进行坐标表示.求出直线a、b的方向向量a、b,平面α、β的法向量m、n.
(2)向量运算
①求直线a、b所成的角,计算cos〈a,b〉;
②求直线a与平面α所成的角,计算cos〈a,m〉;
③求两个平面的夹角的大小,计算cos〈m,n〉.
(3)解释结论
①由于直线a、b所成角θ∈,故cos θ=|cos〈a,b〉|.
②直线a与平面α所成角θ∈,由图形知〈a,m〉与θ的余角相等或互补,故sin θ=|cos〈a,b〉|.
③两个平面的夹角为不大于直角的角,范围θ∈,故cos θ=|cos〈m,n〉|.
2.向量法求空间中的距离
(1)点A,B间的距离.
d=||
(2)点A到直线a的距离
d=,其中B∈a,a是直线a的方向向量.
(3)点A到平面α的距离.
d=,其中B∈α,n是平面α的法向量.
1.下列说法中不正确的是( )
A.平面α的法向量垂直于与平面α共面的所有向量
B.一个平面的所有法向量互相平行
C.如果两个平面的法向量垂直,那么这两个平面也垂直
D.如果a、b与平面α共面且n⊥a,n⊥b,那么n就是平面α的一个法向量
D [选项A,B,C的命题显然是正确的.只有当a、b不共线且a∥α,b∥α时,D才正确.故答案为D.]
2.已知a,b是两异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b且AB=2,CD=1,则直线a,b所成的角为( )
A.30° B.60° C.90° D.45°
B [由于=++,
∴·=(++)·=||=1.
所以cos〈,〉==⇒〈,〉=60°.]
3.正方体ABCDA1B1C1D1中,BB1与平面ACD1所成角的正弦值为( )
A. B.
C. D.
B [设正方体的棱长为1,依题意,建立如图所示的坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),B1(1,1,1)
∴=(-1,0,1),=(-1,1,0)
设平面ACD1的法向量为n=(x,y,z),
∴
令x=1,∴n=(1,1,1),
又∵=(0,0,1),
∴BB1与平面ACD1所成角的正弦值为=.]
4.如图,在正三棱柱ABCA1B1C1中,所有棱长均为1,则点B1到平面ABC1的距离为________.
[如图所示,取AB的中点M,连接CM,C1M,过点C作CD⊥C1M,垂足为D.
∵C1A=C1B,M为AB中点,
∴C1M⊥AB.
∵CA=CB,M为AB中点,
∴CM⊥AB.
又∵C1M∩CM=M,∴AB⊥平面C1CM
又∵AB⊂平面ABC1,
∴平面ABC1⊥平面C1CM,平面ABC1∩平面C1CM=C1M,CD⊥C1M,∴CD⊥平面C1AB,
∴CD的长度即为点C到平面ABC1的距离,即点B1到平面ABC1的距离,在Rt△C1CM中,C1C=1,CM=,C1M=,∴CD=,即点B1到平面ABC1的距离为.]
5.如图,在四棱锥PABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=.
(1)求证:CD⊥平面PAD;
(2)求二面角FAEP的余弦值.
[解] (1)因为PA⊥平面ABCD,所以PA⊥CD.
又因为AD⊥CD,PA∩AD=A,所以CD⊥平面PAD.
(2)过A作AD的垂线交BC于点M,因为PA⊥平面ABCD,所以PA⊥AM,PA⊥AD,如图建立空间直角坐标系Axyz,则A(0,0,0),B(2,-1,0),C(2,2,0),D(0,2,0),P(0,0,2),因为E为PD的中点,
所以E(0,1,1).
所以=(0,1,1),=(2,2,-2),=(0,0,2).
所以==,=+=.
设平面AEF的法向量为n=(x,y,z),
则,
即.
令z=1,则y=-1,x=-1.
于是n=(-1,-1,1).
又因为平面PAD的法向量为p=(1,0,0),
所以cos〈n,p〉==-.
因为二面角FAEP为锐角,所以其余弦值为.