2019-2020学年高中数学课时作业28独立性检验北师大版选修2-3

2019-2020学年高中数学课时作业28独立性检验北师大版选修2-3

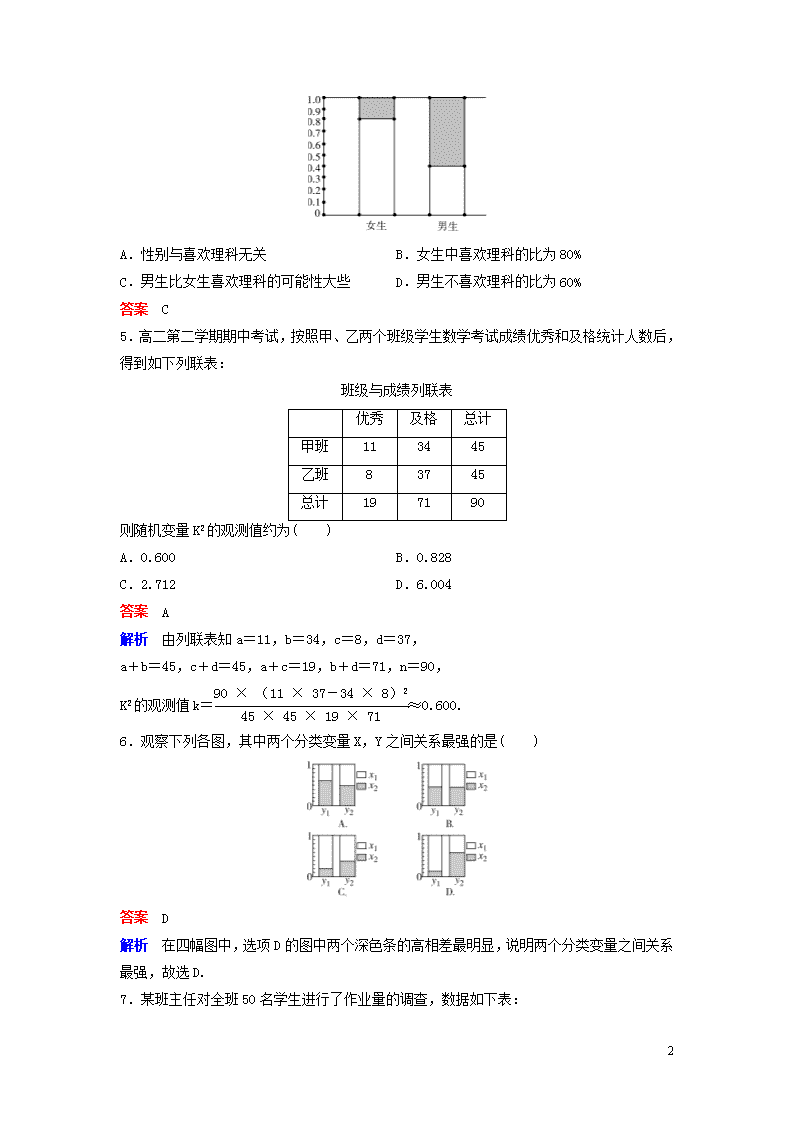
课时作业(二十八)‎ ‎1．在2×2列联表中，两个比值________相差越大，两个分类变量之间的关系越强(　　)‎ A.与　　　　　　 B.与 C.与 D.与 答案　A ‎2．有两个分类变量X与Y的一组数据，由其列联表计算得K2≈4.523，则认为X与Y有关系是错误的可信度为(　　)‎ A．95% B．90%‎ C．5% D．10%‎ 答案　C 解析　P(K2≥3.841)＝0.05.故选C.‎ ‎3．假设两个分类变量X与Y，它们的可能取值分别为{x1，x2}和{y1，y2}，其列联表为 y1‎ y2‎ 总计 x1‎ a b a＋b x2‎ c d c＋d 总计 a＋c b＋d a＋b＋c＋d 对于同一样本的以下各组数据，能说明X与Y有关的可能性最大的一组为(　　)‎ A．a＝5，b＝4，c＝3，d＝2 B．a＝5，b＝3，c＝4，d＝2‎ C．a＝2，b＝3，c＝4，d＝5 D．a＝2，b＝3，c＝5，d＝4‎ 答案　D 解析　(1)利用|ad－bc|越大越有关进行判断；‎ ‎(2)利用与相差越大越有关进行判断．‎ 对于A，|ad－bc|＝|10－12|＝2；对于B，|ad－bc|＝|10－12|＝2；‎ 对于C，|ad－bc|＝|10－12|＝2；对于D，|ad－bc|＝|8－15|＝7.‎ 故选D.‎ ‎4．下面是调查某地区男女中学生喜欢理科的等高条形图，阴影部分表示喜欢理科的百分比，从图可以看出(　　)‎ 12‎ A．性别与喜欢理科无关 B．女生中喜欢理科的比为80%‎ C．男生比女生喜欢理科的可能性大些 D．男生不喜欢理科的比为60%‎ 答案　C ‎5．高二第二学期期中考试，按照甲、乙两个班级学生数学考试成绩优秀和及格统计人数后，得到如下列联表：‎ 班级与成绩列联表 优秀 及格 总计 甲班 ‎11‎ ‎34‎ ‎45‎ 乙班 ‎8‎ ‎37‎ ‎45‎ 总计 ‎19‎ ‎71‎ ‎90‎ 则随机变量K2的观测值约为(　　)‎ A．0.600 B．0.828‎ C．2.712 D．6.004‎ 答案　A 解析　由列联表知a＝11，b＝34，c＝8，d＝37，‎ a＋b＝45，c＋d＝45，a＋c＝19，b＋d＝71，n＝90，‎ K2的观测值k＝≈0.600.‎ ‎6．观察下列各图，其中两个分类变量X，Y之间关系最强的是(　　)‎ 答案　D 解析　在四幅图中，选项D的图中两个深色条的高相差最明显，说明两个分类变量之间关系最强，故选D.‎ ‎7．某班主任对全班50名学生进行了作业量的调查，数据如下表：‎ 12‎ 认为作业量大 认为作业量不大 总计 男生 ‎18‎ ‎9‎ ‎27‎ 女生 ‎8‎ ‎15‎ ‎23‎ 总计 ‎26‎ ‎24‎ ‎50‎ 则学生的性别与认为作业量的大小有关系的把握大约为(　　)‎ A．99% B．95%‎ C．90% D．无充分根据 答案　B 解析　k＝≈5.059>3.841.‎ ‎8．通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：‎ 男 女 总计 爱好 ‎40‎ ‎20‎ ‎60‎ 不爱好 ‎20‎ ‎30‎ ‎50‎ 总计 ‎60‎ ‎50‎ ‎110‎ 由K2＝算得，‎ K2＝≈7.8.‎ 附表：‎ P(K2≥k)‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k ‎3.841‎ ‎6.635‎ ‎10.828‎ 参照附表，得到的正确结论是(　　)‎ A．有99%以上的把握认为“爱好该项运动与性别有关”‎ B．有99%以上的把握认为“爱好该项运动与性别无关”‎ C．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”‎ D．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”‎ 答案　A ‎9．大学生和研究生毕业的一个随机样本给出了关于所获取学位类别与学生性别的分类数据如下表．根据表中数据，有________的把握认为性别与获取学位类别有关．‎ 硕士 博士 总计 12‎ 男 ‎162‎ ‎27‎ ‎189‎ 女 ‎143‎ ‎8‎ ‎151‎ 总计 ‎305‎ ‎35‎ ‎340‎ 答案　99%‎ ‎10．在独立性检验中，选用K2作为统计量，当K2满足条件________时，我们有90%的把握说事件A与B有关．‎ 答案　K2>2.706‎ 解析　由K2的相关规定可知．‎ ‎11．统计推断，当________时，有95%的把握说事件A与B有关；当________时，认为没有充分的证据显示事件A与B是有关的．‎ 答案　K2>3.841，K2≤2.706‎ 解析　结合K2的临界值表可知，‎ 当K2>3.841时有95%的把握说事件A与B有关；‎ 当K2≤2.706时认为没有充分的证明显示事件A与B是有关的．‎ ‎12．有2×2列联表：‎ B B 总计 A ‎54‎ ‎40‎ ‎94‎ A ‎32‎ ‎63‎ ‎95‎ 总计 ‎86‎ ‎103‎ ‎189‎ 由上表可计算K2≈________．‎ 答案　10.76‎ 解析　K2＝≈10.76.‎ ‎13．205份样品分别接种于甲、乙两种培养基上，经过规定的一段时间后，检查培养的效果．结果分为阳性和阴性，资料如下．试分析这两种培养基的培养效果是否有显著差别．‎ 阳性 阴性 总计 甲培养基 ‎36‎ ‎34‎ ‎70‎ 乙培养基 ‎32‎ ‎103‎ ‎135‎ 总计 ‎68‎ ‎137‎ ‎205‎ 解析　由公式得K2的观测值k＝≈15.984，‎ 因为15.984>10.828，K2≥10.828的概率约为0.001，所以拒绝H0.因此有99.9%以上的把握认为这两种培养基的培养效果有显著差异．‎ ‎14．为调查某地区老年人是否需要志愿者提供帮助，‎ 12‎ 用简单随机抽样方法从该地区调查了500位老年人，结果如下：‎ ‎　　　　　　　性别 是否需要志愿者　　　　‎ 男 女 需要 ‎40‎ ‎30‎ 不需要 ‎160‎ ‎270‎ ‎(1)估计该地区老年人中，需要志愿者提供帮助的老年人的比例；‎ ‎(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？‎ ‎(3)根据(2)的结论，能否提出更好的调查方法来估计该地区的老年人中，需要志愿者提供帮助的老年人的比例？说明理由．附：‎ P(K2≥k)‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎　　　　　K2＝ 解析　(1)调查的500位老年人中有70位需要志愿者提供帮助，因此该地区老年人中，需要帮助的老年人的比例的估计值为＝14%.‎ ‎(2)K2＝≈9.967，‎ 因为9.967>6.635，所以有99%的把握认为该地区的老年人是否需要帮助与性别有关．‎ ‎(3)根据(2)的结论可知，该地区的老年人是否需要志愿者提供帮助与性别有关，并且从样本数据能够看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异，因此在调查时，先确定该地区老年人中男女的比例，再把老年人分成男女两层，并采用分层抽样方法比简单随机抽样方法更好．‎ ‎15．针对时下的“韩剧热”，某校团委对“喜欢韩剧和学生性别是否有关”进行了一次调查，其中女生人数是男生人数的，男生喜欢韩剧的人数占男生人数的，女生喜欢韩剧人数占女生人数的.‎ ‎(1)若在犯错误的概率不超过0.05的前提下认为是否喜欢韩剧和性别有关，则男生至少有多少人？‎ ‎(2)若在犯错误的概率不超过0.1的前提下，没有充分的证据显示是否喜欢韩剧和性别有关，则男生至多有多少人？‎ 解析　设男生人数为x，依题意可得列联表如下：‎ 喜欢韩剧 不喜欢韩剧 总计 12‎ 男生 x 女生 总计 x x ‎(1)若在犯错误的概率不超过0.05的前提下认为是否喜欢韩剧和性别有关，则k≥3.841.‎ 由k＝＝x≥3.841，解得x≥10.24.‎ 因为，为整数，所以若在犯错误的概率不超过0.05的前提下认为是否喜欢韩剧和性别有关，则男生至少有12人．‎ ‎(2)在犯错误的概率不超过0.1的前提下，没有充分的证据显示是否喜欢韩剧和性别有关，则k<2.706，由k＝＝x<2.706，解得x<7.216.‎ 因为，为整数，所以，若没有充分的证据显示是否喜欢韩剧和性别有关，则男生至多有6人．‎ ‎1．考察棉花种子经过处理跟生病之间的关系得到如下表数据：‎ 种子处理 种子未处理 总计 得病 ‎32‎ ‎101‎ ‎133‎ 不得病 ‎61‎ ‎213‎ ‎274‎ 总计 ‎93‎ ‎314‎ ‎407‎ 根据以上数据，则(　　)‎ A．种子经过处理跟是否生病有关 B．种子经过处理跟是否生病无关 C．种子是否经过处理决定是否生病 D．以上都是错误的 答案　B 解析　由公式得K2的观测值为k＝≈0.164.‎ ‎2．电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名．如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图．‎ 12‎ 将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性．‎ ‎(1)根据已知条件完成下面的2×2列联表，并据此资料判断在犯错误的概率不超过0.1的前提下能否认为“体育迷”与性别有关？‎ 非体育迷 体育迷 合计 男 女 合计 ‎(2)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率．‎ 解析　(1)由所给的频率分布直方图知，‎ ‎“体育迷”人数为100×(10×0.020＋10×0.005)＝25(人)，‎ ‎“非体育迷”人数为75，则据题意完成2×2列联表：‎ 非体育迷 体育迷 合计 男 ‎30‎ ‎15‎ ‎45‎ 女 ‎45‎ ‎10‎ ‎55‎ 合计 ‎75‎ ‎25‎ ‎100‎ 将2×2列联表中的数据代入公式计算：k＝＝≈3.030.‎ 因为3.030>2.706，在犯错误的概率不超过0.1的前提下认为“体育迷”与性别有关．‎ ‎(2)由所给的频率分布直方图知 ‎“超级体育迷”人数为100×(10×0.005)＝5(人)，‎ 记ai(i＝1，2，3)表示男性，bj(j＝1，2)表示女性，所有可能结果构成的基本事件空间为Ω＝{(a1，a2)，(a1，a3)，(a2，a3)，(a1，b1)，(a2，b1)，(a3，b1)，(a1，b2)，(a2，b2)，(a3，b2)，(b1，b2)}，共有10个基本事件，且每个基本事件出现是等可能的；用A表示事件“任选2人，至少有1名女性”，‎ 则A＝{(a1，b1)，(a2，b1)，(a3，b1)，(a1，b2)，(a2，b2)，(a3，b2)，(b1，b2)}，共有7个基本事件，故“任选2人，至少有1名女性”的概率为P(A)＝.‎ 12‎ ‎3．某县对在职的71名高中数学教师就支持新的数学教材还是支持旧的数学教材做了调查，结果如下表所示：‎ 支持新教材 支持旧教材 合计 具有15年以上教龄的教师 ‎12‎ ‎25‎ ‎37‎ 教龄在15以下的教师 ‎10‎ ‎24‎ ‎34‎ 合计 ‎22‎ ‎49‎ ‎71‎ 根据此资料，你是否认为教龄的长短与支持新的数学教材有关？‎ 解析　由公式得K2＝ ‎＝≈0.08.‎ ‎∵K2<3.841，‎ ‎∴我们没有理由说教龄的长短与支持新的数学教材有关．‎ ‎1．(2012·湖南)设某大学的女生体重y(单位：kg)与身高x(单位：cm)具有线性相关关系，根据一组样本数据(xi，yi)(i＝1，2，…，n)，用最小二乘法建立的回归方程为＝0.85x－85.71，则下列结论中不正确的是(　　)‎ A．y与x具有正的线性相关关系 B．回归直线过样本点的中心(x，y)‎ C．若该大学某女生身高增加1 cm，则其体重约增加0.85 kg D．若该大学某女生身高为170 cm，则可断定其体重必为58.79 kg 答案　D 解析　D项中，若该大学某女生身高为170 cm，则其体重约为0.85×170－85.71＝58.79(kg)．故D项不正确．‎ ‎2．(2011·山东)某产品的广告费用x与销售额y的统计数据如下表：‎ 广告费用x(万元)‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额y(万元)‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ 根据上表可得回归方程＝x＋中的为9.4，据此模型预报广告费用为6万元时销售额为 ‎(　　)‎ A．63.6万元　　　　　　　　 B．65.5万元 C．67.7万元 D．72.0万元 答案　B 12‎ 解析　∵＝－＝－9.4×＝9.1，‎ ‎∴回归方程为＝9.4x＋9.1.‎ 令x＝6，得＝9.4×6＋9.1＝65.5(万元)．‎ ‎3．(2011·陕西)设(x1，y1)，(x2，y2)，…，(xn，yn)是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图)，以下结论中正确的是(　　)‎ A．x和y的相关系数为直线l的斜率 B．x和y的相关系数在0到1之间 C．当n为偶数时，分布在l两侧的样本点的个数一定相同 D．直线l过点(x，y)‎ 答案　D 解析　∵回归直线方程＝＋x中＝y－x，‎ ‎∴＝y－x＋x，当x＝x时＝y，∴直线l过定点(x，y)．‎ ‎4．(2010·湖南)某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是(　　)‎ A．＝－10x＋200 B．＝10x＋200‎ C．＝－10x－200 D．＝10x－200‎ 答案　A 解析　由y与x负相关，排除B、D两项，而C项中＝－10x－200<0不符合题意．‎ ‎5．(2011·广东)某数学老师身高176 cm，他爷爷、父亲和儿子的身高分别是173 cm、170 cm和182 cm.因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为________cm.‎ 答案　185‎ 解析　由题意父亲身高x cm与儿子身高y cm对应关系如下表：‎ x ‎173‎ ‎170‎ ‎176‎ y ‎170‎ ‎176‎ ‎182‎ 则x＝＝173，y＝＝176，‎ 12‎ （xi－）（yi－）＝（173－173）×（170－176）＋（170－173）×（176－176）＋（176－173）（182－176）＝18，‎ （xi－）2＝（173－173）2＋（170－173）2＋（176－173）2＝18.‎ ‎∴＝＝1.∴＝－＝176－173＝3.‎ ‎∴线性回归直线方程为＝x＋＝x＋3.‎ ‎∴可估计孙子身高为182＋3＝185(cm)．‎ ‎6．(2011·辽宁)调查了某地若干户家庭的年收入x(单位：万元)和年饮食支出y(单位：万元)，调查显示年收入x与年饮食支出y具有线性相关关系，并由调查数据得到y对x的回归直线方程：y^＝0.254x＋0.321.由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加________万元．‎ 答案　0.254‎ 解析　家庭收入每增加1万元，对应回归直线方程中的x增加1，相应的y∧的值增加0.254，即年饮食支出平均增加0.254万元．‎ ‎7．(2012·福建)某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：‎ 单价x(元)‎ ‎8‎ ‎8.2‎ ‎8.4‎ ‎8.6‎ ‎8.8‎ ‎9‎ 销量y(件)‎ ‎90‎ ‎84‎ ‎83‎ ‎80‎ ‎75‎ ‎68‎ ‎(1)求回归直线方程＝bx＋a，其中b＝－20，a＝－b x；‎ ‎(2)预计在今后的销售中，销量与单价仍然服从(1)中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？(利润＝销售收入－成本)‎ 解析(1)由于＝(x1＋x2＋x3＋x4＋x5＋x6)＝8.5，‎ ＝(y1＋y2＋y3＋y4＋y5＋y6)＝80.‎ 所以a＝－b＝80＋20×8.5＝250.‎ 从而回归直线方程为＝－20x＋250.‎ ‎(2)设工厂获得的利润为L元，依题意得 L＝x(－20x＋250)－4(－20x＋250)‎ ‎＝－20x2＋330x－1 000‎ ‎＝－20(x－)2＋361.25.‎ 12‎ 当且仅当x＝8.25时，L取得最大值．‎ 故当单价定为8.25元时，工厂可获得最大利润．‎ ‎8．(2014·新课标全国Ⅱ)某地区2007年至2013年农村居民家庭人均纯收入y(单位：千元)的数据如下表：‎ 年份 ‎2007‎ ‎2008‎ ‎2009‎ ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ 年份代号t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 人均纯收入y ‎2.9‎ ‎3.3‎ ‎3.6‎ ‎4.4‎ ‎4.8‎ ‎5.2‎ ‎5.9‎ ‎(1)求y关于t的线性回归方程；‎ ‎(2)利用(1)中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．‎ 附：回归直线的斜率和截距的最小二乘估计公式分别为：‎ 解析　(1)由所给数据计算，得 ＝×(1＋2＋3＋4＋5＋6＋7)＝4，‎ ＝×(2.9＋3.3＋3.6＋4.4＋4.8＋5.2＋5.9)＝4.3，‎ （ti－）2＝9＋4＋1＋0＋1＋4＋9＝28，‎ （ti－）（yi－）＝（－3）×（－1.4）＋（－2）×（－1）＋（－1）×（－0.7）＋0×0.1＋1×0.5＋2×0.9＋3×1.6＝14，‎ ＝y－t＝4.3－0.5×4＝2.3.‎ 所求回归方程为＝0.5t＋2.3.‎ ‎(2)由(1)知，＝0.5>0，故2007年至2013年该地区农村居民家庭人均纯收入逐年增加，平均每年增加0.5千元．‎ 将2015年的年份代号t＝9代入(1)中的回归方程，得＝0.5×9＋2.3＝6.8.‎ 故预测该地区2015年农村居民家庭人均纯收入为6.8千元．‎ 12‎ 12‎