2015届高三理科数学肇庆一模试卷

2015届高三理科数学肇庆一模试卷

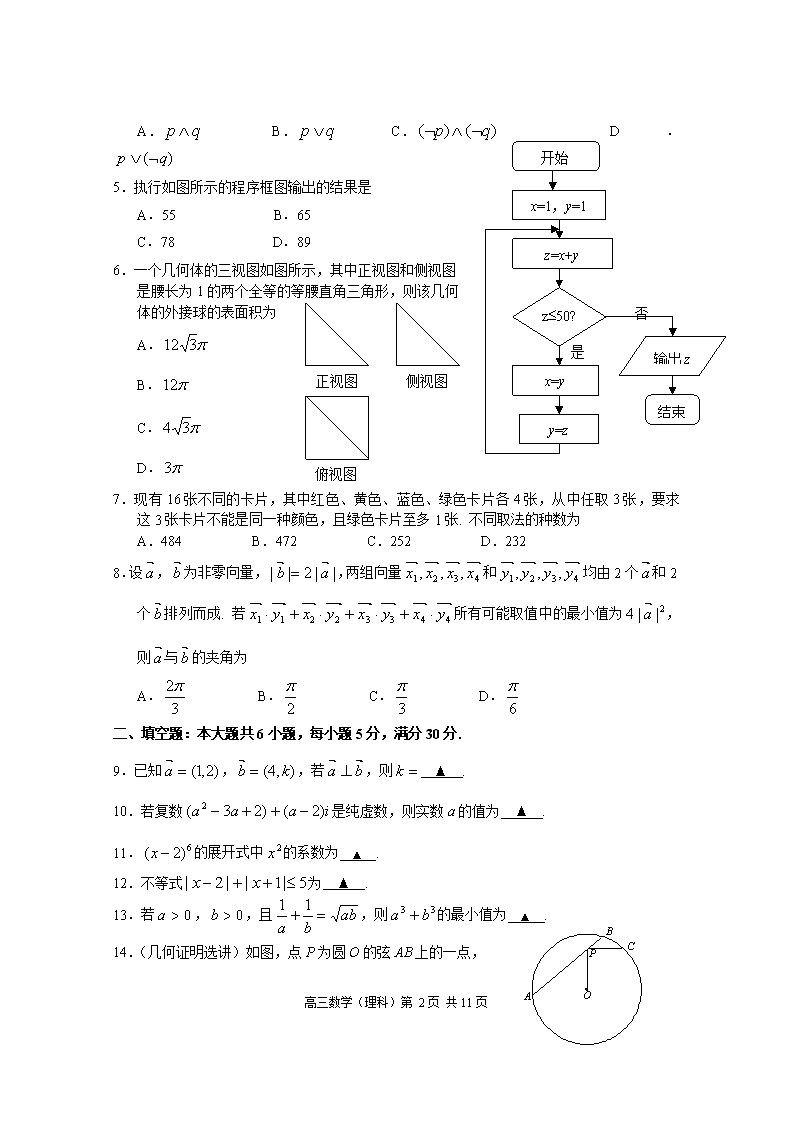
肇庆市中小学教学质量评估 ‎2015届高中毕业班第一次统一检测题 数 学（理科）‎ 本试卷共4页，20小题，满分150分. 考试用时120分钟.‎ 注意事项：‎ ‎1. 答卷前，考生务必用黑色字迹的钢笔或签字笔，将自己所在县（市、区）、姓名、试室号、座位号填写在答题卷上对应位置，再用2B铅笔将准考证号涂黑.‎ ‎2. 选择题每小题选出答案后，用2B铅笔把答题卷上对应题目的答案标号涂黑；如需要改动，用橡皮擦干净后，再选涂其它答案，答案不能写在试卷上或草稿纸上.‎ ‎3. 非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内相应的位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液. 不按以上要求作答的答案无效.‎ 参考公式：锥体的体积公式，其中S为锥体的底面积，为锥体的高. ‎ 球的表面积公式，其中R为球的半径.‎ 线性回归方程中系数计算公式，，其中，表示样本均值.‎ 一、选择题：本大题共8小题，每小题5分，满分40分. 在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．已知全集U={1，2，3，4，5，6}，集合M={1，3，5}，则 A．f B．{1，3，5} C．{2，4，6} D．{1，2，3，4，5，6}‎ ‎2．设条件p：；条件q：，那么p是q的 A．充分条件 B．必要条件 C．充要条件 D．非充分非必要条件 ‎3．‎ A． B． C． D．‎ ‎4．设是非零向量，已知命题p：若，，则；命题q：若，，则. 则下列命题中真命题是 高三数学（理科）第 11页 共11页 A． B． C． D．‎ 开始 x=1，y=1‎ z=x+y z£50?‎ 是 x=y y=z 输出z 结束 否 ‎5．执行如图所示的程序框图输出的结果是 A．55 B．65‎ C．78 D．89‎ ‎6．一个几何体的三视图如图所示，其中正视图和侧视图 是腰长为1的两个全等的等腰直角三角形，则该几何 正视图 侧视图 俯视图 体的外接球的表面积为 A．‎ B．‎ C．‎ D．‎ ‎7．现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张，从中任取3张，要求这3张卡片不能是同一种颜色，且绿色卡片至多1张. 不同取法的种数为 A．484 B．472 C．252 D．232‎ ‎8．设，为非零向量，，两组向量和均由2个和2个排列而成. 若所有可能取值中的最小值为，则与的夹角为 A． B． C． D．‎ 二、填空题：本大题共6小题，每小题5分，满分30分. ‎ ‎9．已知，，若，则 ▲ .‎ ‎10．若复数是纯虚数，则实数a的值为 ▲ .‎ ‎11．的展开式中的系数为 ▲ .‎ ‎12．不等式为 ▲ .‎ ‎13．若，，且，则的最小值为 ▲ .‎ ‎14．（几何证明选讲）如图，点P为圆O的弦AB上的一点，‎ 高三数学（理科）第 11页 共11页 连接PO，过点P作PC^OP，且PC交圆O于C. 若AP=4，‎ PC=2，则PB= ▲ .‎ 三、解答题：本大题共6小题，满分80分. 解答须写出文字说明、证明过程和演算步骤. ‎ ‎15．（本小题满分12分）‎ 为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打篮球时间x（单位：小时）与当天投篮命中率y之间的关系：‎ 时间x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 命中率y ‎0.4‎ ‎0.5‎ ‎0.6‎ ‎0.6‎ ‎0.4‎ ‎（1）求小李这5天的平均投篮命中率；‎ ‎（2）用线性回归分析的方法，预测小李该月6号打6小时篮球的投篮命中率.‎ ‎16．（本小题满分12分）‎ 如图，已知AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，，，，E是PC的中点，F是PB的中点.‎ ‎（1）求证：EF//平面ABC；‎ ‎（2）求证：EF^平面PAC；‎ ‎（3）求PC与平面ABC所成角的大小.‎ ‎17．（本小题满分14分）‎ 某商店根据以往某种玩具的销售记录，绘制了日销售量的频率分布直方图，如图所示.将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立.‎ ‎（1）估计日销售量的众数；‎ ‎（2）求在未来连续3天里，有连续2天的 日销售量都不低于100个且另1天的日销售量低 于50个的概率；‎ ‎（3）用X表示在未来3天里日销售量不低 高三数学（理科）第 11页 共11页 于100个的天数，求随机变量X的分布列，‎ 期望E（X）及方差D（X）.‎ ‎18．（本小题满分14分）‎ 某家电生产企业根据市场调查分析，决定调整新产品生产方案，准备每周（按40个工时计算）生产空调器、彩电、冰箱共120台，且冰箱至少生产20台. 已知生产这些家电产品每台所需工时和每台产值如下表：‎ 家电名称 空调器 彩电 冰箱 工 时 产值/千元 ‎4‎ ‎3‎ ‎2‎ 问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？（以千元为单位）‎ ‎19．（本小题满分14分）‎ 如图，四棱柱中，^底面ABCD，且. 梯形ABCD的面积为6，且AD//BC，AD=2BC，CD=2. 平面与交于点E. ‎ ‎（1）证明：EC//；‎ ‎（2）求三棱锥的体积；‎ ‎（3）求二面角的大小.‎ ‎20．（本小题满分14分）‎ 设a为常数，且.‎ ‎（1）解关于x的不等式；‎ 高三数学（理科）第 11页 共11页 ‎（2）解关于x的不等式组.‎ 肇庆市2015届高中毕业班第一次统测 数学（理科）参考答案及评分标准 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 C A D B A D B C 二、填空题 ‎9．-2 10．1 11．240 12．[-2，3] 13． 14．1‎ 三、解答题 ‎15．（本小题满分12分）‎ 证明：（1）小李这5天的平均投篮命中率为. （4分）‎ ‎（2）小李这5天打篮球的平均时间（小时） （5分）‎ ‎ （7分）‎ ‎ （9分）‎ 所以 （10分）‎ 当x=6时，，故预测小李该月6号打6小时篮球的投篮命中率为0.53. （12分）‎ ‎16．（本小题满分12分）‎ 高三数学（理科）第 11页 共11页 证明：（1）在DPBC中，E是PC的中点，F是PB的中点，所以EF//BC. （1分）‎ 又BCÌ平面ABC，EFË平面ABC，所以EF//平面ABC. （3分）‎ ‎（2）因为AB是⊙O的直径，所以BC^AC. （4分）‎ 在RtDABC中，AB=2，AC=BC，所以. （5分）‎ 因为在DPCB中，，，，‎ 所以，所以BC^PC. （6分）‎ 又PC∩AC=C，所以BC^平面PAC. （7分）‎ 由（1）知EF//BC，所以EF^平面PAC. （8分）‎ ‎（3）解：由（2）知BC^平面PAC，PAÌ平面PAC，所以PA^BC. （9分）‎ 因为在DPAC中，，，，‎ 所以，所以PA^AC. （10分）‎ 又AC∩BC=C，所以PA^平面ABC.‎ 所以ÐPCA为PC与平面ABC所成角. （11分）‎ 在Rt PAC中，，所以ÐPCA=，即PC与平面ABC所成角的大小为. （12分）‎ ‎17．（本小题满分14分）‎ 解：（1）依据日销售量的频率分布直方图可得众数为. （3分）‎ ‎（2）记事件A1：“日销售量不低于100个”， 事件A2：“日销售量低于50个”，事件B：“在未来连续3天里，有连续2天的日销售量都不低于100个且另1天的日销售量低于50个”.‎ 则， （4分）‎ ‎， （5分）‎ ‎. （7分）‎ 高三数学（理科）第 11页 共11页 ‎（3）X的可能取值为0，1，2，3.‎ ‎， （8分）‎ ‎， （9分）‎ ‎， （10分）‎ ‎， （11分）‎ 分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎0.064‎ ‎0.288‎ ‎0.432‎ ‎0.216‎ 因为X~B（3，0.6），所以期望， （12分）‎ 方差. （14分）‎ ‎18．（本小题满分14分）‎ 解：设每周生产空调器x台、彩电y台，则生产冰箱台，产值为z千元，‎ 则依题意得， （4分）‎ 且x，y满足即 （8分）‎ 可行域如图所示. （10分）‎ 解方程组得 即M（10，90）.‎ ‎ （11分）‎ 让目标函数表示的直线在可行域上平移，‎ 可得在M（10，90）处取得最大值，且 高三数学（理科）第 11页 共11页 ‎（千元）. （13分）‎ 答：每周应生产空调器10台，彩电90台，冰箱20台，才能使产值最高，最高产值是350千元. （14分）‎ ‎19．（本小题满分14分）‎ ‎（1）证明：因为，，‎ ‎，所以. （1分）‎ 因为，，‎ ‎，所以. （2分）‎ 又，，‎ ‎，所以. （3分）‎ 又，，‎ 所以EC//. （4分）‎ ‎（2）解：因为，BC//AD，AD=2BC，所以.‎ ‎ （6分）‎ 所以. （8分）‎ ‎（3）解法一：如图，在中，作于F，连接. （9分）‎ 因为^底面ABCD，，‎ 所以.‎ 又，所以.‎ 又，所以. （10分）‎ 所以为二面角的平面角. （11分）‎ 高三数学（理科）第 11页 共11页 由（2）得，所以. （12分）‎ 所以， （13分）‎ 所以，即二面角的大小为. （14分）‎ 解法二：如图，以D为坐标原点，分别为x轴和z轴正方向建立空间直角坐标系.‎ ‎ （9分）‎ 设，BC=a，则AD=2a.‎ 因为，所以.（10分）‎ 所以，， ‎ 所以，. （11分）‎ 设平面的一个法向量，‎ 由，得，所以.（12分）‎ 又平面ABCD的一个法向量， （13分）‎ 所以，所以二面角的大小为. （14分）‎ ‎20．（本小题满分14分）‎ 解：（1）令，解得，. （1分）‎ ‎①当时，解原不等式，得，即其解集为；‎ ‎ （2分）‎ 高三数学（理科）第 11页 共11页 ‎②当时，解原不等式，得无解，即其解集为f ； （3分）‎ ‎③当时，解原不等式，得，即其解集为.‎ ‎ （4分）‎ ‎（2）依（*），令（**），‎ 可得. （5分）‎ ‎①当时，，此时方程（**）无解，解不等式（*），得，故原不等式组的解集为； （6分）‎ ‎②当时，， 此时方程（**）有两个相等的实根，解不等式（*），得，故原不等式组的解集为； （7分）‎ ‎③当时，，此时方程（**）有两个不等的实根，，且，解不等式（*），得或.‎ ‎ （8分）‎ ‎，‎ ‎ （9分）‎ ‎， （10分）‎ 且，‎ ‎ （11分）‎ 所以当，可得；又当，可得，故，（12分）‎ 高三数学（理科）第 11页 共11页 所以ⅰ）当时，原不等式组的解集为；‎ ‎ （13分）‎ ⅱ）当时，原不等式组的解集为f . （14分）‎ 综上，当时，原不等式组的解集为f ；当时，原不等式组的解集为；当时，原不等式组的解集为；当时，原不等式组的解集为.‎ 高三数学（理科）第 11页 共11页