- 2021-06-10 发布 |
- 37.5 KB |
- 3页


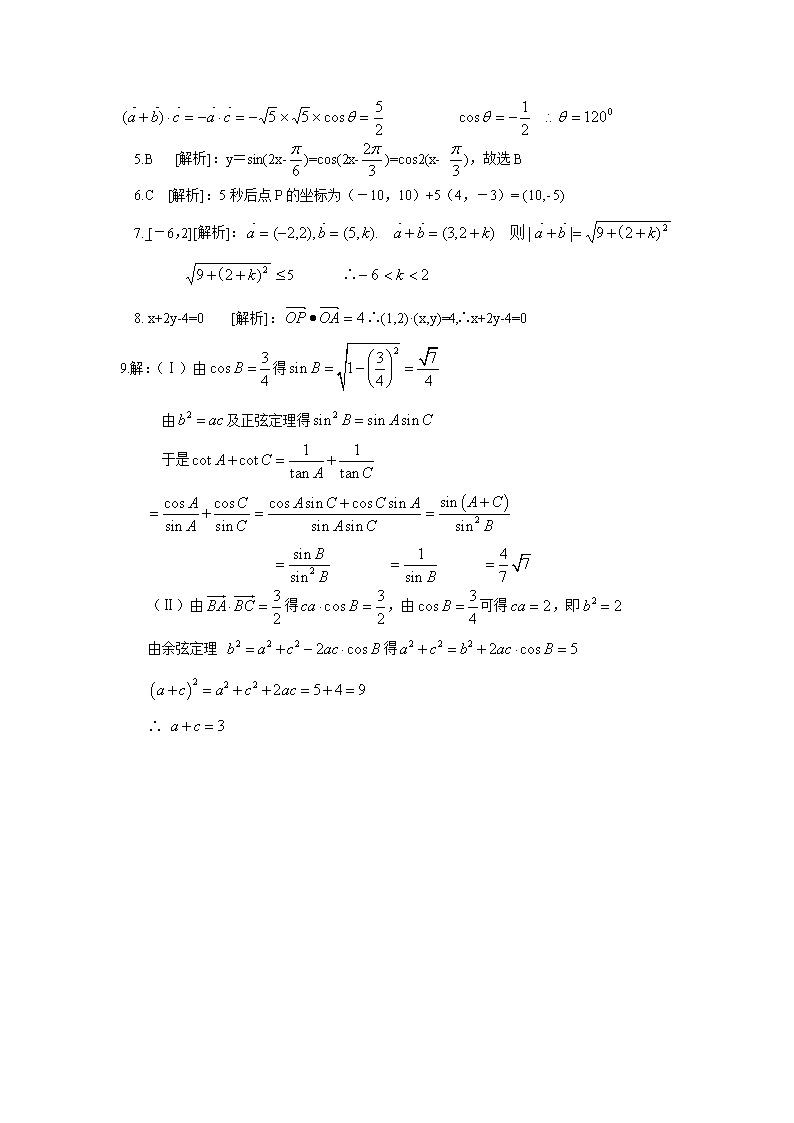
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高三数学复习之30分钟小练习(36)
高三数学复习之 30 分钟小练习(36) 1.若 ,且 ,则向量 与 的夹角为 A 30° B 60° C 120° D 150° 2.P 是△ABC 所在平面上一点,若 ,则 P 是△ABC 的 A 外心 B 内心 C 重心 D 垂心 3.已知平行四边形 ABCD 中, =(3, 7 ), =(-2, 3 ), 对角线 AC, BD 交于 O, 则 的坐标为 A (- , 5) B (- , -5) C ( , -5) D ( , 5) 4. 已知向量 A 30° B 60° C 120° D 150° 5.为了得到函数 y=sin(2x- )的图像,可以将函数 y=cos2x 的图像 A 向右平移 个单位长度 B 向右平移 个单位长度 C 向左平移 个单位长度 D 向左平移 个单位长度 6. 点 P 在平面上作匀速直线运动,速度向量 =(4,-3)(即点 P 的运动方向与 v 相同, 且每秒移动的距离为| |个单位.设开始时点 P 的坐标为(-10,10),则 5 秒后点 P 的坐标 为 A (-2,4) B (-30,25) C (10,-5) D (5,-10) 7.已知向量 不超过 5,则 k 的取值范围是_______ 8.直角坐标平面 中,若定点 与动点 满足 ,则点 P 的轨迹方 程是__________ 9. 中 , 内 角 的 对 边 分 别 是 , 已 知 成 等 比 数 列 , 且 (Ⅰ)求 的值 (Ⅱ)设 ,求 的值。 | | 1,| | 2,a b c a b= = = + c a⊥ a b PAPCPCPBPBPA ⋅=⋅=⋅ AD AB CO 2 1 2 1 2 1 2 1 的夹角为与则若 cacbacba ,2 5)(,5||),4,2(),2,1( =⋅+=−−== 6 π 6 π 3 π 6 π 3 π v v ||).,5(),2,2( bakba +=−= 若 xoy )2,1(A ),( yxP 4=•OAOP ABC∆ A B C、 、 a b c、 、 a b c、 、 3cos 4B = cot cotA C+ 3 2BA BC⋅ = a c+ 参考答案 1.C [解析]:若 ,设向量 与 的夹角为 ∵ ,∴ ,则 ∴ 2.D [ 解 析 ] : ∵ , 则 由 得 同理 ,即 P 是垂心 3.B [ 解 析 ] : =(3, 7 ), =(-2, 3 ), , 则 4.C [ 解 析 ] : , ∵ , ∴ | | 1,| | 2,a b c a b= = = + a b θ c a⊥ 0)( =⋅+ aba 0cos|||||| 2 =⋅+ θbaa 01202 1cos =∴−= θθ PAPCPCPBPBPA ⋅=⋅=⋅ PCPBPBPA ⋅=⋅ ACPBACPBPAPCPB ⊥∴=⋅=−⋅ ,0,0)( 即 ABPCBCPA ⊥⊥ , AD AB )10,1(=+= ADABAC )5,2 1(2 1 −−=−= ACCO θ的夹角为与设 ca )4,2(),2,1( −−== ba ab 2−= 5.B [解析]:y=sin(2x- )=cos(2x- )=cos2(x- ),故选 B 6.C [解析]:5 秒后点 P 的坐标为(-10,10)+5(4,-3)= (10,- 5) 7. [-6,2][解析]: 5 ∴ 8. x+2y-4=0 [解析]: ∴(1,2)·(x,y)=4,∴x+2y-4=0 9.解:(Ⅰ)由 得 由 及正弦定理得 于是 (Ⅱ)由 得 ,由 可得 ,即 由余弦定理 得 ∴ 天 星 教育网(www.tesoon.com) 版权所有 天 星 教育网(www.tesoon.com) 版权所有 天 星 教育网(www.tesoon.com) 版权所有 天 星 教育网(www.tesoon.com) 版权所有 2 5cos55)( =××−=⋅−=⋅+ θcacba 01202 1cos =∴−= θθ 6 π 3 2π 3 π 2)29||)2,3().,5(),2,2( kbakbakba ++=++=+=−= (则 2)29 k++( ≤ 26 <<− k 4=•OAOP 3cos 4B = 23 7sin 1 4 4B = − = 2b ac= 2sin sin sinB A C= 1 1cot cot tan tanA C A C + = + cos cos sin sin A C A C = + cos sin cos sin sin sin A C C A A C += ( ) 2 sin sin A C B += 2 sin sin B B = 1 sin B = 4 77 = 3 2BA BC⋅ = 3cos 2ca B⋅ = 3cos 4B = 2ca = 2 2b = 2 2 2 2 cosb a c ac B= + − ⋅ 2 2 2 2 cos 5a c b ac B+ = + ⋅ = ( )2 2 2 2 5 4 9a c a c ac+ = + + = + = 3a c+ = 天 · 星 o m 权 T e s o o n . c o m 天 星 版 权 t e s o o n 天 · 星 o m 权 天 · 星 o m 权T e s o o n . c o m 天 星 版 权 t e s o o n t e s o o n t e s o o n 天 星查看更多