高中立体几何练习题根据历年高考题改编

高中立体几何练习题根据历年高考题改编

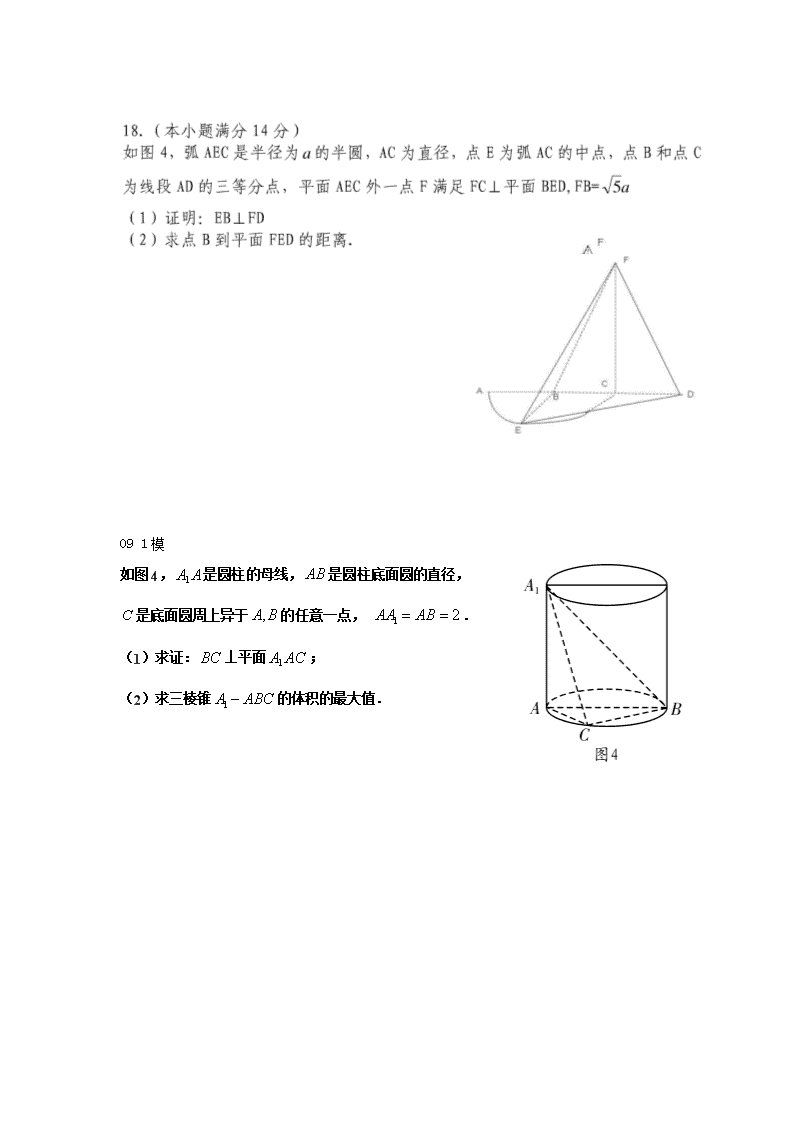
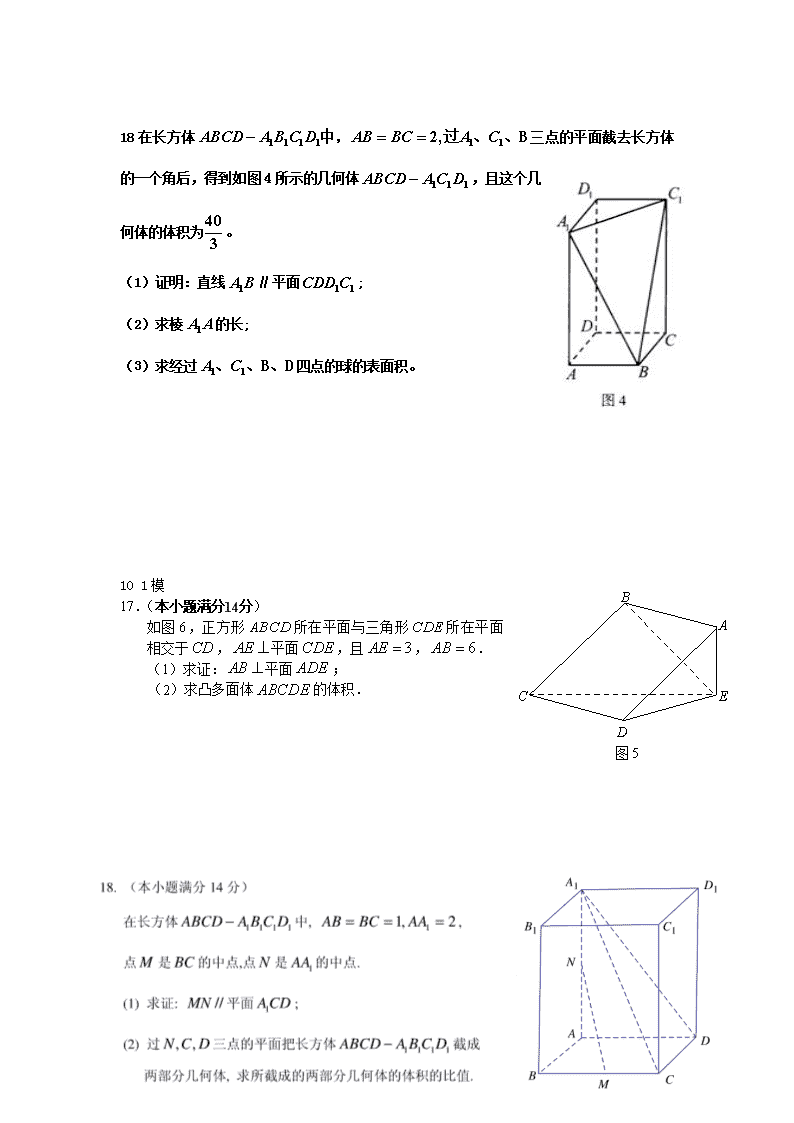
立体几何复习精选 一． 选择 ‎10 1模 ‎5．已知：直线与平面内无数条直线垂直，：直线与平面垂直．则是的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 三． 大题 ‎18．如图5所示，四棱锥的底面是半径为的圆的内接四边形，其中是圆的直径，，，．‎ ‎（1）求线段的长；‎ ‎（2）若，求三棱锥的体积． ‎C P A B 图5‎ D ‎09 1模 如图4，是圆柱的母线，是圆柱底面圆的直径，‎ 是底面圆周上异于的任意一点， ．‎ ‎（1）求证：⊥平面；‎ ‎（2）求三棱锥的体积的最大值．‎ ‎ ‎ ‎18在长方体三点的平面截去长方体的一个角后，得到如图4所示的几何体，且这个几何体的体积为。‎ ‎（1）证明：直线∥平面;‎ ‎（2）求棱的长;‎ ‎（3）求经过四点的球的表面积。‎ A B C D ‎ E ‎ 图5‎ ‎10 1模 ‎17．（本小题满分14分）‎ 如图6，正方形所在平面与三角形所在平面相交于，平面，且，．‎ ‎ （1）求证：平面；‎ ‎（2）求凸多面体的体积．‎ 如图，在四棱锥中，底面是矩形，平面，，．以的中点为球心、为直径的球面交于点．‎ ‎（1）求证：平面⊥平面；‎ ‎（2）求点到平面的距离．‎ ‎ ‎ ‎ ‎ ‎18．解：（1）是圆的直径，又，‎ ‎，；‎ ‎（2）在中，‎ ‎，又底面 三棱锥的体积为 ‎（1）证明：∵是底面圆周上异于、的一点，且为底面圆的直径，‎ ‎∴． …… 2分 ‎∵⊥平面，平面，‎ ‎∴. …… 4分 ‎∵平面,平面,‎ ‎∴平面． …… 6分 ‎（2）解法1:设,在Rt△ 中，（0＜x＜2， ‎ 故（0＜x＜2, ‎ ‎ 即． ‎ ‎　∵,　‎ ‎∴当，即时，三棱锥的体积的最大值为． ‎ ‎ 解法2: 在Rt△ 中，, ‎ ‎ ‎ ‎ . 当且仅当时等号成立，此时 ∴三棱锥的体积的最大值为. ‎ ‎（1）证法1：如图，连结，∵是长方体，‎ ‎∴且．∴四边形是平行四边形．‎ ‎∴．∵平面，平面，‎ ‎∴平面． ‎ ‎（2）解：设，∵几何体的体积为，‎ ‎∴即，‎ 即，解得．∴的长为4． ‎ ‎（3）如图，连结，设的中点为，连 ‎∵是长方体，∴平面．‎ ‎∵平面，∴．‎ ‎∴．同理．‎ ‎∴．‎ ‎∴经过，，，四点的球的球心为点． ‎ ‎∵． ‎ ‎∴．‎ 故经过，，，四点的球的表面积为． ‎ ‎10-1‎ ‎1）证明：∵平面，平面，‎ ‎∴． ‎ 在正方形中，，‎ ‎∵，∴平面．‎ ‎∵，‎ ‎∴平面．‎ A ‎ B ‎ C ‎ D ‎ E ‎ A ‎ B ‎ C ‎ D ‎ E ‎ F ‎ 最后：（1）证：依题设，Ｍ在以ＢＤ为直径的球面上，则ＢＭ⊥ＰＤ.‎ 因为ＰＡ⊥平面ＡＢＣＤ，则ＰＡ⊥ＡＢ，又ＡＢ⊥ＡＤ，‎ 所以ＡＢ⊥平面ＰＡＤ，则ＡＢ⊥ＰＤ，因此有ＰＤ⊥平面ＡＢＭ，所以平面ＡＢＭ⊥‎ 平面ＰＣＤ.‎ ‎（3）因为O是BD的中点，则O点到平面ABM的距离等于D点到平面ABM距离的一半，由（1）知，ＰＤ⊥平面ＡＢＭ于M，则|DM|就是D点到平面ABM距离.‎ 因为在Rt△PAD中，，，所以为中点，，则O点到平面ABM的距离等于。‎ ‎11-1‎