徐州市2015中考撷秀三模数学

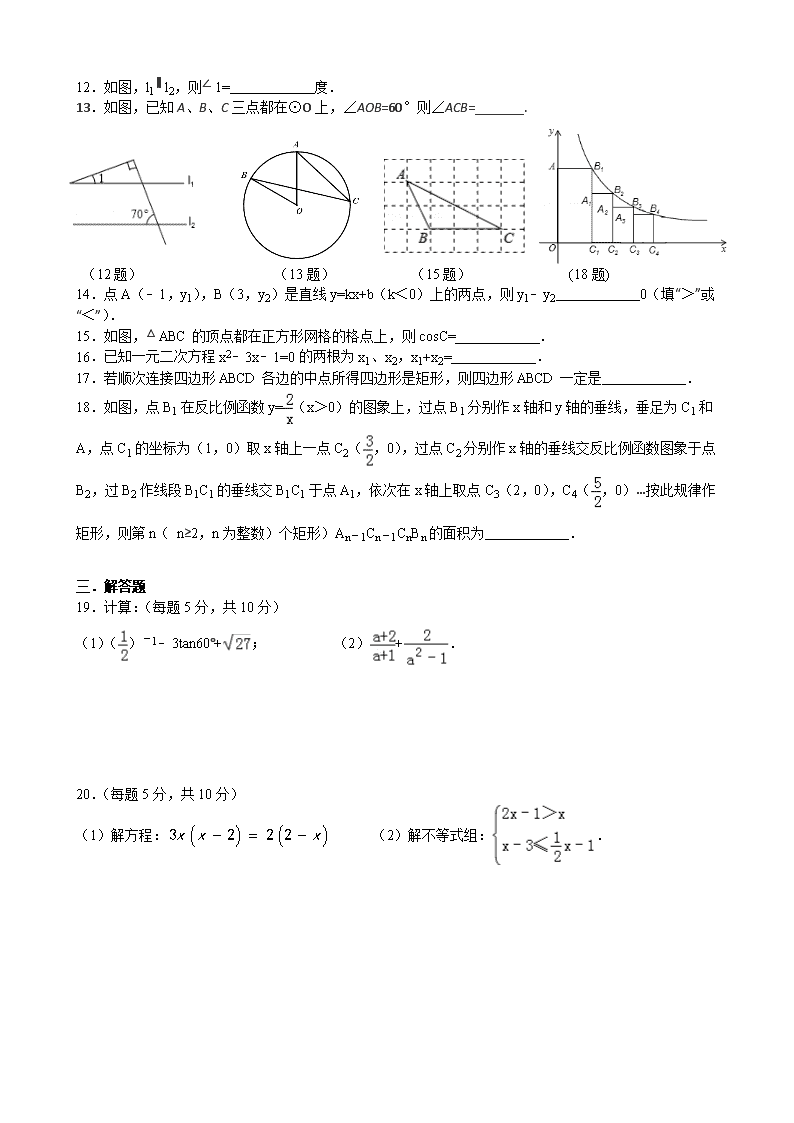
徐州市2015中考撷秀三模数学

撷秀初级中学2014-2015学年度第二学期最后一卷 九年级数学试卷 一．选择题（每题3分，共24分）‎ ‎1．﹣1.5的绝对值是（　　）‎ ‎　‎ A．‎ ‎0‎ B．‎ ‎﹣1.5‎ C．‎ ‎1.5‎ D．‎ ‎2．下列几何体的主视图与众不同的是（　　）‎ A B C D ‎ ‎3．下列运算结果正确的是（　　） （第5题） （第7题）‎ ‎　‎ A．‎ a2•a3=a6‎ B．‎ ‎（a2）3=a5‎ C．‎ x6÷x2=x4‎ D．‎ a2+a5=2a3‎ ‎4．在平面直角坐标系中，反比例函数y=的图象的两支分别在（　　）‎ ‎　‎ A．‎ 第一、三象限 B．‎ 第一、二象限 C．‎ 第二、四象限 D．‎ 第三、四象限 ‎5．如图，圆锥模具的母线长为10cm，底面半径为5cm，则这个圆锥模具的侧面积是（　　）‎ ‎　‎ A．‎ ‎10πcm2‎ B．‎ ‎50πcm2‎ C．‎ ‎100πcm2‎ D．‎ ‎150πcm2‎ ‎6．某销售公司有营销人员15人，销售部为了制定某种商品的月销售量定额，统计了这15人某月的销售量，如下表所示：‎ 每人销售件数 ‎1800‎ ‎510‎ ‎250‎ ‎210‎ ‎150‎ ‎120‎ 人数 ‎1‎ ‎1‎ ‎3‎ ‎5‎ ‎3‎ ‎2‎ 那么这15位销售人员该月销售量的平均数、众数、中位数分别是（　　）‎ ‎　‎ A．‎ ‎320，210，230‎ B．‎ ‎320，210，210‎ C．‎ ‎206，210，210‎ D．‎ ‎206，210，230‎ ‎7．如图，△ABC中，AD、BE是两条中线，则S△EDC：S△ABC=（　　）‎ ‎　‎ A．‎ ‎1：2‎ B．‎ ‎2：3‎ C．‎ ‎1：3‎ D．‎ ‎1：4‎ ‎8．如图，将边长1cm的等边三角形ABC沿直线l向右翻动(不滑动)，点B从开始到结束，所经过的长度为( )‎ A、 B、‎ C、 D、3cm 二．填空题（每题3分，共30分）‎ ‎9．因式分解：a2+2a=　　　　　　．‎ ‎10．震惊世界的MH370失联事件发生后第30天，中国“海巡01”轮在南印度洋海域搜索过程中首次侦听到疑是飞机黑匣子的脉冲信号，探测到的信号所在海域水深4500米左右，其中4500用科学记数法表示为　　　　　　．‎ ‎11.使有意义的x的取值范围是 ．‎ ‎12．如图，l1∥ l2，则∠ 1=　　　　　　度．‎ ‎13．如图，已知A、B、C三点都在⊙O上，∠AOB=60°则∠ACB=_______.‎ ‎　‎ ‎　‎ ‎（12题） （13题） （15题） (18题)‎ ‎14．点A（﹣1，y1），B（3，y2）是直线y=kx+b（k＜0）上的两点，则y1﹣y2　　　　　　0（填“＞”或“＜”）．‎ ‎15．如图，△ ABC的顶点都在正方形网格的格点上，则cosC=　　　　　　．‎ ‎16．已知一元二次方程x2﹣3x﹣1=0的两根为x1、x2，x1+x2=　　　　　　．‎ ‎17．若顺次连接四边形ABCD各边的中点所得四边形是矩形，则四边形ABCD一定是　　　　　　．‎ ‎18．如图，点B1在反比例函数y=（x＞0）的图象上，过点B1分别作x轴和y轴的垂线，垂足为C1和A，点C1的坐标为（1，0）取x轴上一点C2（，0），过点C2分别作x轴的垂线交反比例函数图象于点B2，过B2作线段B1C1的垂线交B1C1于点A1，依次在x轴上取点C3（2，0），C4（，0）…按此规律作矩形，则第n（ n≥2，n为整数）个矩形）An﹣1Cn﹣1CnBn的面积为　　　　　　．‎ 三．解答题 ‎19．计算：（每题5分，共10分）‎ ‎（1）（）﹣1﹣3tan60°+； （2）+．‎ ‎20．（每题5分，共10分）‎ ‎（1）解方程： （2）解不等式组：．‎ ‎21．（本题7分）某校九年级所有学生参加2011年初中毕业英语口语、听力自动化考试，我们从中随机抽取了部分学生的考试成绩，将他们的成绩进行统计后分为A、B、C、D四等，并将统计结果绘制成如下的统计图，请你结合图中所给信息解答下列问题：‎ ‎（说明：A级：25分～30分；B级：20分～24分；C级：15分～19分；D级：15分以下）‎ ‎（1）请把条形统计图补充完整；‎ ‎（2）扇形统计图中D级所占的百分比是　　　　　　；‎ ‎（3）扇形统计图中A级所在的扇形的圆心角度数是　　　　　　；‎ ‎（4）若该校九年级有850名学生，请你估计全年级A级和B级的学生人数共约为　　　　　　人．‎ ‎22．（本题7分）在不透明的布袋中装有1个白球，2个红球，它们除颜色外其余完全相同．‎ ‎（1）从袋中任意摸出两个球，试用树状图或表格列出所有等可能的结果，并求摸出的球恰好是两个红球的概率；‎ ‎（2）若在布袋中再添加x个白球，充分搅匀，从中摸出一个球，使摸到白球的概率为，求添加的白球个数x．‎ ‎23．（本题8分）如图，在□ABCD中，E、F分别为边AB、CD的中点，连接DE、BF、BD．‎ ‎（1）求证：△ADE≌△CBF．‎ ‎（2）当AD⊥BD时，请你判断四边形BFDE的形状，并说明理由．‎ ‎　‎ ‎24. （本题8分）从徐州到某市可乘坐普通列车或高铁．已知高铁的行驶路程是400千米，普通列车的行驶路程是520千米．如果高铁的平均速度是普通列车平均速度的2.5倍，且乘坐高铁比乘坐普通列车少用3小时，求高铁的平均速度是多少千米/时？‎ ‎25．（本题8分）如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°． 已知原传送带AB长为4米．‎ ‎（1）求新传送带AC的长度．‎ ‎（2）如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点5米的货物MNQP是否需要挪走，并说明理由．‎ 参考数据：．‎ ‎　‎ ‎　‎ A B F O G C E D ‎26. （本题8分）如图，在Rt△ABC中，∠A＝90°，O是BC边上一点，以O为圆心的半圆与AB边相切于点D，与AC、BC边分别交于点E、F、G，连结OD．已知BD＝2，AE＝3，tan∠BOD＝．‎ ‎（1）求⊙O的半径OD；‎ ‎（2）求证：AE是⊙O的切线；‎ ‎（3）求图中两部分阴影面积的和．‎ ‎27．（本题10分）如图1，矩形ABCD中，点P从A出发，以3cm/s的速度沿边A→B→C→D→A匀速运动；同时点Q从B出发，沿边B→C→D匀速运动，当其中一个点到达终点时两点同时停止运动，设点P运动的时间为t s．△APQ的面积s（cm2）与t（s）之间函数关系的部分图象由图2中的曲线段OE与线段EF给出．‎ ‎（1）点Q运动的速度为　　　　　　cm/s，a﹦　　　　　　cm2；‎ ‎（2）若BC﹦3cm，‎ ‎①求t＞3时S的函数关系式；‎ ‎②在图（2）中画出①中相应的函数图象．‎ ‎　‎ ‎28．（本题10分）如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，A、C两点的坐标分别为（4，0），（﹣2，3），抛物线W经过O、A、C三点，D是抛物线W的顶点．‎ ‎（1）求抛物线W的解析式及顶点D的坐标；‎ ‎（2）将抛物线W和□OABC一起先向右平移4个单位后，再向下平移m（0＜m＜3）个单位，得到抛物线W′和□O′A′B′C′，在向下平移的过程中，设□O′A′B′C′与□OABC的重叠部分的面积为S，试探究：当m为何值时S有最大值，并求出S的最大值；‎ ‎（3）在（2）的条件下，当S取最大值时，设此时抛物线W′的顶点为F，若点M是x轴上的动点，点N是抛物线W′上的动点，试判断是否存在这样的点M和点N，使得以D、F、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．‎