中考数学压轴题精选测试题12

中考数学压轴题精选测试题12

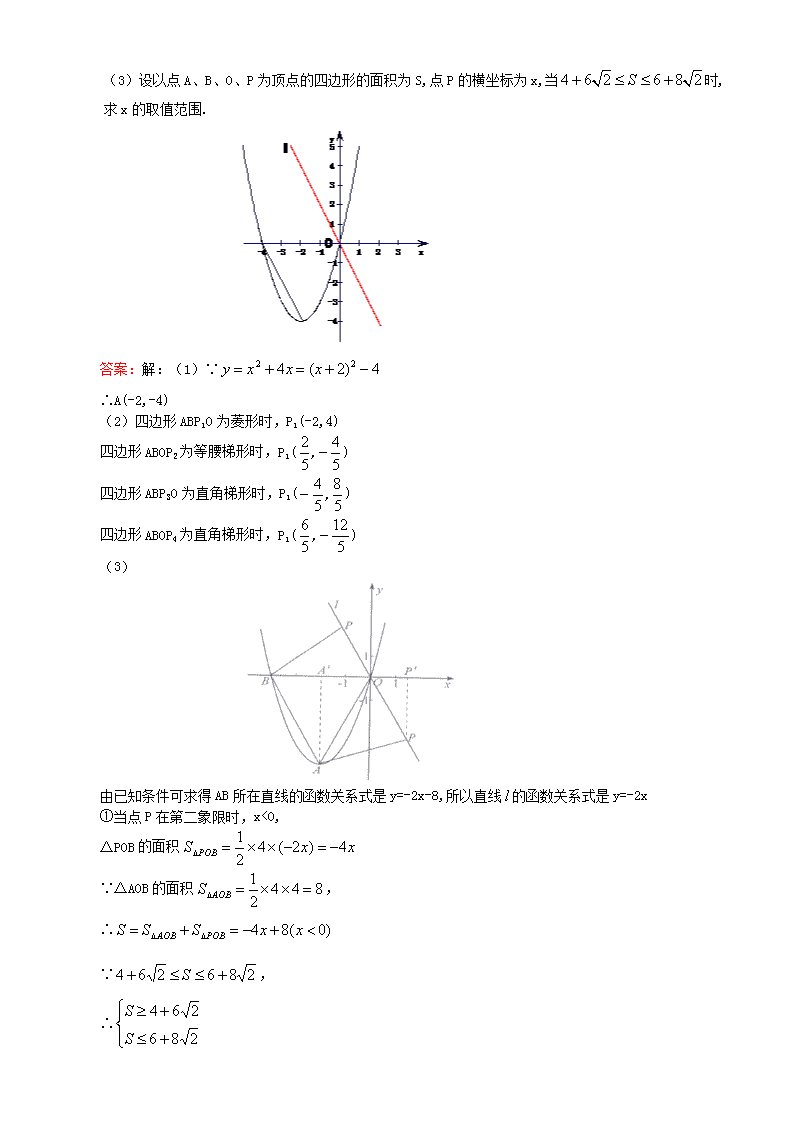
中考数学分类汇编 压轴题(12)‎ ‎1、如图，在平面直角坐标系中，点，点分别在轴，轴的正半轴上，且满足．‎ ‎（1）求点，点的坐标．‎ ‎（2）若点从点出发，以每秒1个单位的速度沿射线运动，连结．设的面积为，点的运动时间为秒，求与的函数关系式，并写出自变量的取值范围．‎ ‎（3）在（2）的条件下，是否存在点，使以点为顶点的三角形与相似？若存在，请直接写出点的坐标；若不存在，请说明理由．‎ 答案：解：（1）‎ ‎，‎ ‎，‎ 点，点分别在轴，轴的正半轴上 ‎（2）求得 ‎（每个解析式各1分，两个取值范围共1分）‎ ‎（3）；；；‎ ‎2、(2008 湖北 天门)如图①，在平面直角坐标系中，A点坐标为(3，0)，B点坐标为(0，4)．动点M从点O出发，沿OA方向以每秒1个单位长度的速度向终点A运动；同时，动点N从点A出发沿AB方向以每秒个单位长度的速度向终点B运动．设运动了x秒．‎ ‎(1)点N的坐标为(________________，________________)；(用含x的代数式表示)‎ ‎(2)当x为何值时，△AMN为等腰三角形？‎ ‎(3)如图②，连结ON得△OMN，△OMN可能为正三角形吗？若不能，点M的运动速度不变，试改变点N的运动速度，使△OMN为正三角形，并求出点N的运动速度和此时x的值．‎ O M A x N B y 图①‎ O Maaaaa A x N B y 图②‎ 答案：解：(1)N()‎ ‎(2)①AM=AN ‎,,,‎ ‎②MN=AM ‎ ‎ ‎(舍去)或 ‎③MN=AN ‎,‎ ‎(3)不能 当N()时，△OMN为正三角形 由题意可得：,解得：‎ 点N的速度为：‎ ‎3、(2008江苏常州)如图,抛物线与x轴分别相交于点B、O,它的顶点为A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.‎ ‎（1）求点A的坐标;‎ ‎（2）以点A、B、O、P为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P的坐标;‎ ‎（3）设以点A、B、O、P为顶点的四边形的面积为S,点P的横坐标为x,当时,求x的取值范围. ‎ ‎ ‎ 答案：解：（1）∵‎ ‎∴A(-2,-4)‎ ‎（2）四边形ABP1O为菱形时，P1(-2,4)‎ 四边形ABOP2为等腰梯形时，P1()‎ 四边形ABP3O为直角梯形时，P1()‎ 四边形ABOP4为直角梯形时，P1()‎ ‎（3）‎ ‎ ‎ 由已知条件可求得AB所在直线的函数关系式是y=-2x-8,所以直线的函数关系式是y=-2x ‎①当点P在第二象限时，x<0,‎ ‎△POB的面积 ‎∵△AOB的面积，‎ ‎∴‎ ‎∵，‎ ‎∴‎ 即 ∴‎ ‎∴x的取值范围是 ‎②当点P在第四象限是，x>0,‎ 过点A、P分别作x轴的垂线，垂足为A′、P′‎ 则四边形POA′A的面积 ‎∵△AA′B的面积 ‎∴‎ ‎∵，‎ ‎∴ 即 ∴‎ ‎∴x的取值范围是 ‎4、（2008广西南宁）随着绿城南宁近几年城市建设的快速发展，对花木的需求量逐年提高。某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润与投资量成正比例关系，如图①所示；种植花卉的利润与投资量成二次函数关系，如图②所示（注：利润与投资量的单位：万元）‎ ‎（1）分别求出利润与关于投资量的函数关系式；‎ ‎（2）如果这位专业户以8万元资金投入种植花卉和树木，他至少获得多少利润？他能获取的最大利润是多少？‎ ‎（注意：在试题卷上作答无效）‎ 答案：解：（1）设=,由图①所示，函数=的图像过（1，2），所以2=，‎ 故利润关于投资量的函数关系式是=；‎ 因为该抛物线的顶点是原点，所以设=，由图12-②所示，函数=的图像过（2，2），‎ 所以，‎ 故利润关于投资量的函数关系式是；‎ ‎（2）设这位专业户投入种植花卉万元（），‎ 则投入种植树木（）万元，他获得的利润是万元，根据题意，得 ‎=+==‎ 当时，的最小值是14；‎ 因为，所以 所以 所以 所以，即，此时 当时，的最大值是32.‎ ‎5、（2008安徽芜湖）如图，已知 ，，现以A点为位似中心，相似比为9:4，将OB向右侧放大，B点的对应点为C．‎ ‎（1）求C点坐标及直线BC的解析式;‎ ‎（2）一抛物线经过B、C两点，且顶点落在x轴正半轴上，求该抛物线的解析式并画出函数图象;‎ ‎（3）现将直线BC绕B点旋转与抛物线相交与另一点P，请找出抛物线上所有满足到直线AB距离为的点P．‎ ‎ ‎ 答案：解:‎ ‎（1）过C点向x轴作垂线，垂足为D，由位似图形性质可知：‎ ‎△ABO∽△ACD， ∴．‎ 由已知，可知： ．‎ ‎∴．∴C点坐标为．‎ ‎ 直线BC的解析是为： ‎ 化简得： ‎ ‎（2）设抛物线解析式为，由题意得： ， ‎ 解得： ‎ ‎∴解得抛物线解析式为或．‎ 又∵的顶点在x轴负半轴上，不合题意，故舍去．‎ ‎∴满足条件的抛物线解析式为 ‎（准确画出函数图象）‎ ‎（3） 将直线BC绕B点旋转与抛物线相交与另一点P，设P到 直线AB的距离为h，‎ 故P点应在与直线AB平行，且相距的上下两条平行直线和上．‎ 由平行线的性质可得：两条平行直线与y轴的交点到直线BC的距离也为．‎ 如图，设与y轴交于E点，过E作EF⊥BC于F点，‎ 在Rt△BEF中，，‎ ‎∴．∴可以求得直线与y轴交点坐标为 同理可求得直线与y轴交点坐标为 ‎∴两直线解析式；．‎ 根据题意列出方程组： ⑴；⑵‎ ‎∴解得：；；；‎ ‎∴满足条件的点P有四个，它们分别是，，，.‎ ‎6、 （2008山东烟台）如图，抛物线交轴于A、B两点，交轴于M点.抛物线向右平移2个单位后得到抛物线，交轴于C、D两点.‎ ‎（1）求抛物线对应的函数表达式；‎ ‎（2）抛物线或在轴上方的部分是否存在点N，使以A，C，M，N为顶点的四边形是平行四边形.若存在，求出点N的坐标；若不存在，请说明理由；‎ ‎（3）若点P是抛物线上的一个动点（P不与点A、B重合），那么点P关于原点的对称点Q是否在抛物线上，请说明理由.‎ ‎ ‎ 答案：‎ ‎7、（2008浙江台州）如图，在矩形中，，，点是边上的动点（点不与点，点重合），过点作直线，交边于点，再把沿着动直线对折，点的对应点是点，设的长度为，与矩形重叠部分的面积为．‎ ‎（1）求的度数；‎ ‎（2）当取何值时，点落在矩形的边上？‎ ‎（3）①求与之间的函数关系式；‎ ‎②当取何值时，重叠部分的面积等于矩形面积的？‎ D Q C B P R A B A D C ‎（备用图1）‎ B A D C ‎（备用图2）‎ 答案：解：（1）如图，四边形是矩形，．‎ 又，，，‎ ‎，．‎ ‎，．‎ ‎，．‎ D Q C B P R A ‎（图1）‎ ‎（2）如图1，由轴对称的性质可知，，‎ ‎，．‎ 由（1）知，，‎ ‎，．‎ ‎，，．‎ 在中，根据题意得：，‎ 解这个方程得：．‎ ‎（3）①当点在矩形的内部或边上时，‎ ‎，，‎ ‎，当时，‎ 当在矩形的外部时（如图2），，‎ D Q C B P R A ‎（图2）‎ F E 在中，，‎ ‎，‎ 又，，‎ 在中，‎ ‎，．‎ ‎，‎ ‎，‎ 当时，．‎ 综上所述，与之间的函数解析式是：．‎ ‎②矩形面积，当时，函数随自变量的增大而增大，所以的最大值是，而矩形面积的的值，‎ 而，所以，当时，的值不可能是矩形面积的；‎ 当时，根据题意，得：‎ ‎，解这个方程，得，因为，‎ 所以不合题意，舍去．‎ 所以．‎ 综上所述，当时，与矩形重叠部分的面积等于矩形面积的．‎ ‎8、（2008四川自贡）抛物线的顶点为M，与轴的交点为A、B（点 B在点A的右侧），△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b.若关 于的一元二次方程有两个相等的实数根.‎ ‎（1）判断△ABM的形状，并说明理由.‎ ‎（2）当顶点M的坐标为（－2，－1）时，求抛物线的解析式，并画出该抛物线的大致图形.‎ ‎（3）若平行于轴的直线与抛物线交于C、D两点，以CD为直径的圆恰好与轴相切，求该圆的圆心坐标.‎ 答案：解：（1）令，得 由勾股定理的逆定理和抛物线的对称性知△ABM是一个以、为直角边的等腰直角三角形 ‎（2）设 ‎∵△ABM是等腰直角三角形 ‎∴斜边上的中线等于斜边的一半 又顶点M(－2，－1)‎ ‎∴，即AB＝2‎ ‎∴A(－3，0)，B(－1，0)‎ 将B(－1，0) 代入中得 ‎∴抛物线的解析式为，即 图略 ‎（3）设平行于轴的直线为 解方程组 得， （‎ ‎∴线段CD的长为 ‎∵以CD为直径的圆与轴相切 据题意得 ‎∴‎ 解得 ‎ ‎∴圆心坐标为和 ‎9、（2008海南）如图，已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C，直线y=-2x-1经过抛物线上一点B(-2,m)，且与y轴、直线x=2分别交于点D、E.‎ ‎（1）求m的值及该抛物线对应的函数关系式；‎ ‎（2）求证：① CB=CE ；② D是BE的中点；‎ ‎（3）若P(x，y)是该抛物线上的一个动点，是否存在这样的点P,使得PB=PE,若存在，试求出所有符合条件的点P的坐标；若不存在，请说明理由 ‎ ‎A B C O D E x y x=2‎ 答案：解：（1）∵ 点B(-2,m)在直线y=-2x-1上，‎ ‎∴m=-2×(-2)-1=3. ∴ B(-2,3)‎ ‎∵ 抛物线经过原点O和点A，对称轴为x=2，‎ ‎∴ 点A的坐标为(4,0) . ‎ 设所求的抛物线对应函数关系式为y=a(x-0)(x-4). ‎ 将点B(-2,3)代入上式，得3=a(-2-0)(-2-4)，∴ .‎ ‎∴ 所求的抛物线对应的函数关系式为，即.‎ ‎（2）①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1) E(2,-5).‎ ‎ 过点B作BG∥x轴，与y轴交于F、直线x=2交于G，‎ ‎ 则BG⊥直线x=2，BG=4.‎ 在Rt△BGC中，BC=.‎ ‎∵ CE=5，‎ A B C O D E x y x=2‎ G F H ‎∴ CB=CE=5. ‎ ‎②过点E作EH∥x轴，交y轴于H，‎ 则点H的坐标为H(0,-5).‎ 又点F、D的坐标为F(0,3)、D(0,-1)，‎ ‎∴ FD=DH=4，BF=EH=2，∠BFD=∠EHD=90°.‎ ‎∴ △DFB≌△DHE （SAS），‎ ‎∴ BD=DE.‎ 即D是BE的中点. ‎ ‎（3）存在. ‎ 由于PB=PE，∴ 点P在直线CD上，‎ ‎∴ 符合条件的点P是直线CD与该抛物线的交点.‎ 设直线CD对应的函数关系式为y=kx+b.‎ 将D(0,-1) C(2,0)代入，得. 解得 .‎ ‎∴ 直线CD对应的函数关系式为y=x-1.‎ ‎∵ 动点P的坐标为(x，)，‎ ‎∴ x-1=. ‎ 解得 ，. ∴ ，.‎ ‎∴ 符合条件的点P的坐标为(，)或(，).‎ ‎10、（2008甘肃兰州）如图1，是一张放在平面直角坐标系中的矩形纸片，为原点，点在轴的正半轴上，点在轴的正半轴上，，．‎ ‎（1）在边上取一点，将纸片沿翻折，使点落在边上的点处，求两点的坐标；‎ ‎（2）如图2，若上有一动点（不与重合）自点沿方向向点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为秒（），过点作的平行线交于点，过点作的平行线交于点．求四边形的面积与时间之间的函数关系式；当取何值时，有最大值？最大值是多少？‎ y x B C O A D E 图1‎ y x B C O A D E 图2‎ P M N ‎（3）在（2）的条件下，当为何值时，以为顶点的三角形为等腰三角形，并求出相应的时刻点的坐标．‎ 答案：解：（1）依题意可知，折痕是四边形的对称轴，‎ 在中，，．‎ ‎．．‎ 点坐标为（2，4）．‎ 在中，， 又．‎ ‎ ． 解得：．‎ 点坐标为 ‎（2）如图①，．‎ ‎，又知，，‎ ‎， 又．‎ 而显然四边形为矩形．‎ ‎，又 当时，有最大值．‎ ‎（3）（i）若以为等腰三角形的底，则（如图①）‎ 在中，，，为的中点，‎ y x B C O A D E 图①‎ P M N F ‎．‎ 又，为的中点．‎ 过点作，垂足为，则是的中位线，‎ ‎，，‎ 当时，，为等腰三角形．‎ 此时点坐标为．‎ ‎（ii）若以为等腰三角形的腰，则（如图②）‎ y x B C O A D E 图②‎ P M N F 在中，．‎ 过点作，垂足为．‎ ‎，．‎ ‎．‎ ‎，．‎ ‎，，‎ 当时，（），此时点坐标为．‎ 综合（i）（ii）可知，或时，以为顶点的三角形为等腰三角形，相应点的坐标为或．‎ ‎11、（2008广东中山）将两块大小一样含30°角的直角三角板，叠放在一起，使得它们的斜边 AB重合，直角边不重合，已知AB=8，BC=AD=4，AC与BD相交于点E，连结CD．‎ ‎（1）填空：如图1，AC= ，BD= ；四边形ABCD是 梯形.‎ ‎（2）请写出图9中所有的相似三角形（不含全等三角形）.‎ ‎（3）如图2若以AB所在直线为轴，过点A垂直于AB的直线为轴建立如图10的平面直角坐标系，保持ΔABD不动，将ΔABC向轴的正方向平移到ΔFGH的位置，FH与BD相交于点P，设AF=t，ΔFBP面积为S，求S与t之间的函数关系式，并写出t的取值值范围.‎ D C B A E 图1‎ ‎ ‎E D C H F G B A P y x 图10‎ ‎2‎ 答案：解：（1），，等腰；‎ ‎ （2）共有9对相似三角形.‎ ‎①△DCE、△ABE与△ACD或△BDC两两相似，分别是：△DCE∽△ABE，△DCE∽△ACD，△DCE∽△BDC，△ABE∽△ACD，△ABE∽△BDC；(有5对)‎ ‎②△ABD∽△EAD，△ABD∽△EBC；(有2对)‎ ‎③△BAC∽△EAD，△BAC∽△EBC；(有2对)‎ 所以，一共有9对相似三角形.‎ ‎（3）由题意知，FP∥AE，‎ ‎ ∴ ∠1＝∠PFB，‎ 又∵ ∠1＝∠2＝30°，‎ ‎ ∴ ∠PFB＝∠2＝30°,‎ ‎∴ FP＝BP.‎ 过点P作PK⊥FB于点K，则.‎ ‎ ‎ ‎∵ AF＝t，AB＝8，‎ ‎∴ FB＝8－t，.‎ 在Rt△BPK中，. ‎ ‎∴ △FBP的面积，‎ ‎∴ S与t之间的函数关系式为：‎ ‎ ，或. ‎ t的取值范围为：.‎ ‎12、（2008山东东营、菏泽）在△ABC中，∠A＝90°，AB＝4，AC＝3，M是AB上的动点（不与A，B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN．令AM＝x． ‎ ‎（1）用含x的代数式表示△ＭNP的面积S； ‎ ‎（2）当x为何值时，⊙O与直线BC相切？ ‎ ‎（3）在动点M的运动过程中，记△ＭNP与梯形BCNM重合的面积为y，试求y关于x的函数表达式，并求x为何值时，y的值最大，最大值是多少？‎ A B C M N P 图 1‎ O A B C M N D 图 2‎ O A B C M N P 图 3‎ O 答案：解：（1）∵MN∥BC，∴∠AMN=∠B，∠ANM＝∠C． ‎ A B C M N P 图 1‎ O ‎∴ △AMN ∽ △ABC．‎ ‎∴ ，即．‎ ‎∴ AN＝x． ‎ ‎∴ =．（0＜＜4） ‎ ‎（2）如图2，设直线BC与⊙O相切于点D，连结AO，OD，则AO =OD =MN．‎ ‎ ‎A B C M N D 图 2‎ O Q 在Rt△ABC中，BC ＝=5．‎ 由（1）知 △AMN ∽ △ABC． ‎ ‎∴ ，即． ‎ ‎∴ ，‎ ‎∴ ．‎ 过M点作MQ⊥BC 于Q，则． ‎ 在Rt△BMQ与Rt△BCA中，∠B是公共角，‎ ‎∴ △BMQ∽△BCA．‎ ‎∴ ．‎ ‎∴ ，． ‎ ‎∴ x＝． ‎ ‎∴ 当x＝时，⊙O与直线BC相切． ‎ A B C M N P 图 3‎ O ‎（3）随点M的运动，当P点落在直线BC上时，连结AP，则O点为AP的中点．‎ ‎∵ MN∥BC，∴ ∠AMN=∠B，∠AOM＝∠APC．‎ ‎∴ △AMO ∽ △ABP． ‎ ‎∴ ． AM＝MB＝2． ‎ 故以下分两种情况讨论： ‎ ① 当0＜≤2时，． ‎ ‎∴ 当＝2时， ‎ ‎ ② 当2＜＜4时，设PM，PN分别交BC于E，F．‎ A B C M N P 图 4‎ O E F ‎∵ 四边形AMPN是矩形， ‎ ‎∴ PN∥AM，PN＝AM＝x． ‎ 又∵ MN∥BC， ‎ ‎∴ 四边形MBFN是平行四边形． ‎ ‎∴ FN＝BM＝4－x． ‎ ‎∴ ． ‎ 又△PEF ∽ △ACB． ‎ ‎∴ ．‎ ‎∴ ． ‎ ‎＝.‎ 当2＜＜4时，． ‎ ‎∴ 当时，满足2＜＜4，．‎ 综上所述，当时，值最大，最大值是2．‎ ‎13、 （2008新疆建设兵团）某工厂要赶制一批抗震救灾用的大型活动板房．如图，板房一面 的形状是由矩形和抛物线的一部分组成，矩形长为12m，抛物线拱高为5.6m．‎ ‎（1）在如图所示的平面直角坐标系中，求抛物线的表达式．‎ ‎（2）现需在抛物线AOB的区域内安装几扇窗户，窗户的底边在AB上，每扇窗户宽1.5m，高1.6m，相邻窗户之间的间距均为0.8m，左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m．请计算最多可安装几扇这样的窗户？‎ ‎ ‎ 答案：解：（1）设抛物线的表达式为 ‎ 点在抛物线的图象上．‎ ‎∴‎ ‎ ‎ ‎∴抛物线的表达式为 ‎ ‎（2）设窗户上边所在直线交抛物线于C、D两点，D点坐标为（k，t）‎ 已知窗户高1.6m，∴‎ ‎（舍去）‎ ‎∴（m）‎ 又设最多可安装n扇窗户 ‎∴ ‎ ‎．‎ 答：最多可安装4扇窗户．‎ ‎（本题不要求学生画出4个表示窗户的小矩形）‎ ‎14、(2008江苏镇江)理解发现 阅读以下材料：‎ 对于三个数，用表示这三个数的平均数，用表示这三个数中最小的数．例如：‎ ‎；；‎ 解决下列问题：‎ ‎（1）填空： ；‎ 如果，则的取值范围为．‎ ‎（2）①如果，求；‎ ‎②根据①，你发现了结论“如果，那么 （填的大小关系）”．证明你发现的结论；‎ ‎③运用②的结论，填空：‎ 若，则 ．‎ x y O ‎（3）在同一直角坐标系中作出函数，，的图象（不需列表描点）．通过观察图象，填空：的最大值为 ．‎ 答案：（1），.‎ ‎（2）①．‎ 法一：．‎ 当时，则，则，．‎ 当时，则，则，（舍去）．‎ 综上所述：．‎ 法二：，‎ ‎ ．‎ ‎②‎ 证明：，‎ 如果，则，．‎ 则有，即．‎ ‎．‎ 又，．且．‎ ‎．‎ 其他情况同理可证，故．‎ ‎③‎ ‎（3）作出图象．‎ x y O P ‎1‎ ‎15、(2008江苏镇江)探索研究 如图，在直角坐标系中，点为函数在第一象限内的图象上的任一点，点的坐标为，直线过且与轴平行，过作轴的平行线分别交轴，于，连结交轴于，直线交轴于．‎ ‎（1）求证：点为线段的中点；‎ ‎（2）求证：①四边形为平行四边形；‎ ‎②平行四边形为菱形；‎ ‎（3）除点外，直线与抛物线有无其它公共点？并说明理由．‎ ‎ ‎x l Q C P A O B H R y 答案：‎ ‎（1）法一：由题可知．‎ ‎，，‎ ‎．‎ ‎，即为的中点．‎ 法二：，，．‎ 又轴，．‎ ‎（2）①由（1）可知，，‎ ‎，，‎ ‎．‎ ‎，‎ 又，四边形为平行四边形．‎ ‎②设，轴，则，则．‎ 过作轴，垂足为，在中，‎ ‎．‎ 平行四边形为菱形．‎ ‎（3）设直线为，由，得，代入得：‎ ‎ 直线为．‎ 设直线与抛物线的公共点为，代入直线关系式得：‎ ‎，，解得．得公共点为．‎ 所以直线与抛物线只有一个公共点． ‎ ‎16、(2008浙江金华) 如图1，在平面直角坐标系中，己知ΔAOB是等边三角形，点A的坐标是(0，4)，点B在第一象限，点P是x轴上的一个动点，连结AP，并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD.‎ ‎（1）求直线AB的解析式；‎ ‎（2）当点P运动到点（，0）时，求此时DP的长及点D的坐标；‎ ‎（3）是否存在点P，使ΔOPD的面积等于，若存在，请求出符合条件的点P的坐标；若不存在，请说明理由。‎ ‎ ‎ 答案：解：（1）作BE⊥OA，‎ ‎ ∴ΔAOB是等边三角形 ‎∴BE=OB·sin60o=，‎ ‎∴B(,2)‎ ‎∵A(0,4),设AB的解析式为,所以,解得,的以直线AB的解析式为 ‎（2）由旋转知，AP=AD, ∠PAD=60o,‎ ‎∴ΔAPD是等边三角形，PD=PA=‎ ‎ ‎ 如图，作BE⊥AO,DH⊥OA,GB⊥DH,显然ΔGBD中∠GBD=30°‎ ‎∴GD=BD=,DH=GH+GD=+=,‎ ‎∴GB=BD=,OH=OE+HE=OE+BG=‎ ‎∴D(,)‎ ‎(3)设OP=x,则由（2）可得D()‎ 若ΔOPD的面积为：‎ 解得：‎ 所以P(,0)‎ O C x A C1‎ F1‎ E1‎ B1‎ B F E y ‎17、（2008湖北荆州）如图，等腰直角三角形纸片ABC中，AC＝BC＝4，∠ACB＝90º，直角边AC在x轴上，B点在第二象限，A（1，0），AB交y轴于E，将纸片过E点折叠使BE与EA所在直线重合，得到折痕EF（F在x轴上），再展开还原沿EF剪开得到四边形BCFE，然后把四边形BCFE从E点开始沿射线EA平移，至B点到达A点停止.设平移时间为t（s），移动速度为每秒1个单位长度，平移中四边形BCFE与△AEF重叠的面积为S.‎ ‎ （1）求折痕EF的长；‎ ‎（2）是否存在某一时刻t使平移中直角顶点C经过抛物线的顶点？若存在，求出t值；若不存在，请说明理由；‎ ‎ （3）直接写出S与t的函数关系式及自变量t的取值范围.‎ ‎ ‎ 答案：‎ ‎ ‎ ‎∥BA 交Y轴于P，‎ P ‎18、（2008上海）已知，，（如图）．是射线 上的动点（点与点不重合），是线段的中点．‎ ‎（1）设，的面积为，求关于的函数解析式，并写出函数的定义域；‎ ‎（2）如果以线段为直径的圆与以线段为直径的圆外切，求线段的长；‎ ‎（3）联结，交线段于点，如果以为顶点的三角形与相似，求线段的长．‎ B A D M E C B A D C 备用图 答案：解：（1）取中点，联结，‎ 为的中点，，．‎ 又，．‎ ‎，得；‎ ‎（2）由已知得．‎ 以线段为直径的圆与以线段为直径的圆外切，‎ ‎，即．‎ 解得，即线段的长为；‎ ‎（3）由已知，以为顶点的三角形与相似，‎ 又易证得．‎ 由此可知，另一对对应角相等有两种情况：①；②．‎ ‎①当时，，．．‎ ‎，易得．得；‎ ‎②当时，，．‎ ‎．又，．‎ ‎，即，得．‎ 解得，（舍去）．即线段的长为2．‎ 综上所述，所求线段的长为8或2．‎ ‎19.（本题满分12分）‎ 如图，直角梯形中，∥,为坐标原点，点在轴正半轴上，点在轴正半轴上，点坐标为（2，2），∠= 60°，于点.动点从点出发，沿线段向点运动，动点从点出发，沿线段向点运动，两点同时出发，速度都为每秒1个单位长度.设点运动的时间为秒.‎ （1） 求的长；‎ （2） 若的面积为（平方单位）. 求与之间的函数关系式.并求为何值时，‎ 的面积最大，最大值是多少？‎ （1） 设与交于点.①当△为等腰三角形时，求（2）中的值.‎ ‎ ②探究线段长度的最大值是多少，直接写出结论.‎ 答案:‎ 解：（1）∵∥‎ ‎ ∴ ‎ ‎ 在中， ,‎ ‎ ∴， ‎ ‎∴ 而 ‎ ∴为等边三角形 ‎ ∴…（3分）‎ ‎（2）∵‎ ‎∴ ‎ ‎∴‎ ‎= （）…………………………（6分）‎ 即 ‎∴当时，………………………………………（7分）‎ ‎（3）①若为等腰三角形，则：‎ ‎（i）若， ‎ ‎ ∴∥ ‎ ‎∴ 即 解得：‎ 此时………………………………（8分）‎ ‎（ii）若，‎ ‎ ∴‎ 过点作，垂足为，则有：‎ 即 解得：‎ 此时……………………………………（9分）‎ ‎（iii）若，‎ ‎∴∥‎ 此时在上，不满足题意.……………………………………………（10分）‎ ‎ ②线段长的最大值为……………………………………………………(12分)‎ ‎20、如图，在中，是的中点，以为直径的交的三边，交点分别是点．的交点为，且，．‎ ‎（1）求证：．‎ ‎（2）求的直径的长．‎ ‎（3）若，以为坐标原点，所在的直线分别为轴和轴，建立平面直角坐标系，求直线的函数表达式．‎ E A D G B F C O M 答案：（1）连接DF ‎ ‎∵CD是圆直径 ∴∠CFD=90°即DF⊥BC ‎ ‎∵∠ACB=90°∴DF ∥AC ‎∴∠BDF=∠A ‎∵在⊙O中∠BDF=∠GEF ∴∠GEF=∠A ‎(2) ∵D是Rt△ABC斜边AB的中点, ‎ ‎∴DC=DA ‎ ‎ ∴∠DCA=∠A 又由(1)知∠GEF=∠A ∴∠DCA=∠GEF 又∵∠OME=∠EMC ∴△OME与△EMC相似 ‎∴ ∴ ‎ 又∵= ∴==96 ‎ ‎∵MD：CO=2:5 ∴OM：MD=3：2 ∴ OM：MC=3：8‎ 设OM=3 MC=8 ∴ ∴=2‎ 直径CD=10x=20‎ ‎(3) ∵Rt△ABC斜边AB的中线CD=20 ∴AB=40‎ ‎ ∵在Rt△ABC中,cos∠B=0.6= ∴BC=24 ∴ AC=32‎ 设直线AB的函数表达式为 根据题意得 A (32,0) B(0,24)‎ ‎ 解得 ‎ ‎∴ ‎ ‎ ‎ ‎∴直线AB的函数解析式为 ‎ ‎21、 (2008台湾) 如图，圆O1、圆O2、圆O3三圆两两相切，为圆O1、圆O2的公切线，为半圆，且分别与三圆各切于一点。若圆O1、圆O2的半径均为1，则圆O3的半径为何？( ) ‎ A B O1‎ O2‎ O3‎ ‎ ‎ A. 1 B. C. －1 D. ＋1‎ 答案：C