2020年中考数学专题复习：三大几何变换

2020年中考数学专题复习：三大几何变换

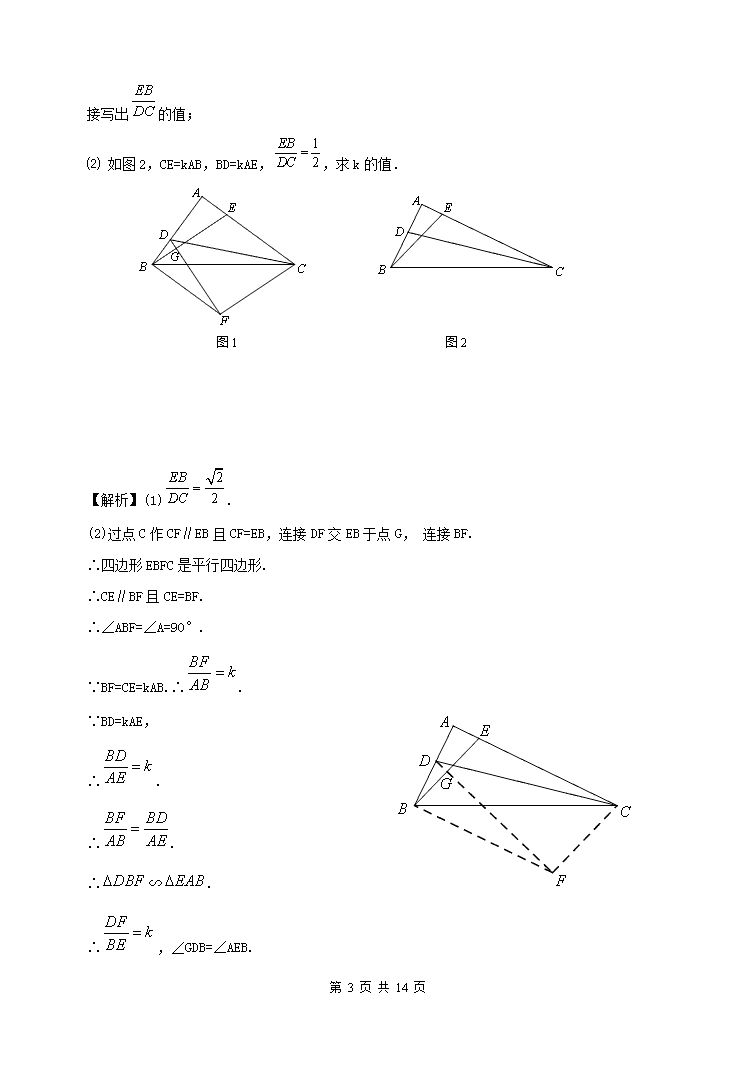
‎ ‎ ‎ ‎ 三大几何变换 知识互联网 ‎[来^%&源@:中#教网]‎ 题型一：平移变换 思路导航 平移一般是在需要同时移动两条线段或元素的时候，才考虑的方法．‎ 典题精练 ‎[来源:zzst%^ep#*.c~om]‎ 已知：如图，正方形中，是上一点，于点．⑴ 求证：．‎ ‎⑵ 求证：．‎ 第 13 页 共 14 页 ‎ ‎ 延长到点，使得，连接、．‎ ‎⑴ ∵，‎ ‎∴四边形为平行四边形[中国#@*教~育出&版网]‎ ‎∴，‎ 又∵，∴‎ ‎∴‎ 在和中 ‎∴‎ ‎∴‎ ‎⑵ 由⑴知道为等腰直角三角形 ‎∴‎ 在中，‎ 当时，取到等号．‎ ‎[ww^w#*.~zzste@p.com]‎ 在Rt△ABC中，∠A=90°，D.E分别为AB.AC上的点．[来源:zzst&ep%#.c^o@m]‎ ‎⑴ 如图1，CE=AB，BD=AE，过点C作CF∥‎ 第 13 页 共 14 页 EB，且CF=EB，连接DF交EB于点G，连接BF，请你直接写出的值；‎ ‎⑵ 如图2，CE=kAB，BD=kAE，，求k的值．‎ 图2‎ 图1‎ ‎[中国教育出*@&%^版网]‎ ‎[来源:中%^教&网@#]‎ ‎[来源*:中^教%网@#]‎ ‎【解析】(1).‎ ‎(2)过点C作CF∥EB且CF=EB，连接DF交EB于点G， 连接BF.‎ ‎∴四边形EBFC是平行四边形.‎ ‎∴CE∥BF且CE=BF.‎ ‎∴∠ABF=∠A=90°.[www.z&^zs#tep.c*o~m]‎ ‎∵BF=CE=kAB.∴.‎ ‎∵BD=kAE，‎ ‎∴.‎ ‎∴.‎ ‎∴∽.[来源~:zzs^*te%@p.com]‎ ‎∴，∠GDB=∠AEB.[来源^:&*@中~教网]‎ 第 13 页 共 14 页 ‎∴∠DGB=∠A=90°.‎ ‎∴∠GFC=∠BGF=90°.[来@&源#:~中*教网]‎ ‎∵.[来源#:^中国教%育出~*版网]‎ ‎∴.‎ ‎∴k=.‎ 题型二：轴对称变换 典题精练 ‎⑴如图，已知正方形纸片的边长为，的半径为，圆心在正方形的中心上，将纸片按图示方式折叠，使恰好与相切于点（与除切点外无重叠部分），延长交边于点，则的长是 ．‎ ‎⑵将弧沿弦折叠交直径于点，若，则的长是______________．‎ ‎⑴ 过点作于．‎ 则四边形是矩形，∴，‎ 设，则根据对称性可知 ‎∴，[www.z^z&@ste*p.co~m]‎ 在中，，‎ ‎∴，即，[来#&%^源:@中教网]‎ 第 13 页 共 14 页 解得，∴．‎ ‎⑵ 将半圆还原，点关于的对称点为，‎ 作于．‎ 根据“翻折”的性质可知，‎ 则 ‎∵，‎ 则，‎ BC2=BH·AB ‎∴．‎ 把正方形沿着折叠使点落在上，交于点，已知正方形的边长为，求的周长．‎ ‎[来%*源:中@教网~&]‎ 在上取点，使，连接．‎ ‎∵，∴‎ 由翻折得对称性可知 ‎∴[来%源:#z~&zstep@.com]‎ 在和中 第 13 页 共 14 页 ‎∴[中&国教育#*~出^版网]‎ ‎∴，‎ 在和中 ‎[来源:z&zstep^.com~@#]‎ ‎∴‎ ‎∴‎ ‎∴的周长为．‎ 题型三：旋转变换 典题精练 在Rt△ABC中，AB=BC，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，将三角板绕点O旋转．‎ ‎⑴ 当点O为AC中点时，[w^ww.zz&ste@p%.com*]‎ ‎①如图1， 三角板的两直角边分别交AB，BC于E.F两点，连接EF，猜想线段AE.CF与EF之间存在的等量关系（无需证明）；[来@^%~源#:中国教育出版网]‎ ‎②如图2， 三角板的两直角边分别交AB，BC延长线于E.F两点，连接EF，判断①中的猜想是否成立．若成立，请证明；若不成立，请说明理由；‎ ‎⑵ 当点O不是AC中点时，如图3，，三角板的两直角边分别交AB，BC于E.F两点，若 第 13 页 共 14 页 ‎，求的值．‎ C O B A O E 图1‎ F B A O C E F ‎ ‎ A B C E F 图2‎ 图3‎ ‎[来^源:中国教育出#~*版%网]‎ C B A O E F ‎【解析】（1）[来源:z#@zs%tep.^com*]‎ 猜想：.‎ 成立.‎ 证明：连结OB.[来@源:中#&%~国教育出版网]‎ ‎∵AB=BC ， ∠ABC=90°，O点为AC的中点，‎ ‎∴，∠BOC=90°，∠ABO=∠BCO=45°.[来源:中国教育出版&^@网*~]‎ ‎∵∠EOF=90°，∴∠EOB=∠FOC. 又∵∠EBO=∠FCO，‎ ‎∴△OEB≌△OFC（ASA）.∴BE=CF.‎ 又∵BA=BC， ∴AE=BF.‎ 在RtΔEBF中，∵∠EBF=90°， ..[www%.@^zzst&#ep.com]‎ ‎（2）解：如图，过点O作OM⊥AB于M，ON⊥BC于N.‎ A O ‎ ‎ B C E F M N ‎∵∠B=90°， ∴∠MON=90°.‎ ‎∵∠EOF=90°，‎ ‎∴∠EOM=∠FON.‎ ‎∵∠EMO=∠FNO=90°，∴△OME∽△ONF.‎ ‎∴‎ ‎∵△AOM和△OCN为等腰直角三角形，‎ 第 13 页 共 14 页 ‎∴△AOM∽△OCN ∴.‎ ‎∵， ∴.‎ ‎[来源@:^zz&st*ep#.com]‎ 和是绕点旋转的两个相似三角形，其中与、与为对应角．‎ ‎⑴如图1，若和分别是以与为顶角的等腰直角三角形，且两三角形旋转到使点、、在同一条直线上的位置时，请直接写出线段与线段的关系；[中&国教育出版#*@%网]‎ ‎⑵若和为含有角的直角三角形，且两个三角形旋转到如图2的位置时，试确定线段与线段的关系，并说明理由；[ww~w.zz@st^ep&.#com]‎ ‎⑶若和为如图3的两个三角形，且，，在绕点旋转的过程中，直线与夹角的度数是否改变？若不改变，直接用含、的式子表示夹角的度数；若改变，请说明理由．‎ ‎⑴ 线段与线段的关系是．‎ ‎⑵ 如图2，连接、并延长，设交点为点．‎ ‎∵ ，∴，∴．‎ ‎∵，∴，．∴ ．‎ ‎∴ ．∴．[www.zz#%&step^@.com]‎ 在中，，‎ 第 13 页 共 14 页 ‎∵，∴．‎ 又∵∴，‎ ‎∴．‎ ‎∵，∴，‎ ‎∴， ∴，∴．[来&%源:中教网~@^]‎ 即．‎ ‎⑶ 在绕点旋转的过程中，直线与夹角度数不改变，度．‎ 复习巩固 题型一 平移变换 巩固练习 如图，已知，，若，则的度数为______．‎ ‎. 通过作平行线平移角，使角与角之间联系起来．‎ A 如下图，两条长度为的线段和相交于点，且，求证：．‎ 第 13 页 共 14 页 ‎ ‎ 考虑将、和集中到同一个三角形中，以便运用三角形的不等关系．‎ 作且，则四边形是平行四边形，从而．‎ ‎（教师可告诉学生：一组对边平行且相等的四边形是平行四边形），‎ 在中可得，‎ 即．‎ 由于，，‎ 所以是等边三角形，故，所以．‎ ‎[来~*源:中&国教育出版网#@]‎ 题型二 轴对称变换 巩固练习 如图矩形纸片，，，上有一 点，，上有一点，，过作 交于，将纸片折叠，使点与点重合，折 痕与交于点，则的长是________cm．‎ ‎. 解法：过Q作QM⊥DC，设QP=x，∴QE=x，∵DE=2，∴[来源:中国教育^%#出版&网@]‎ ‎∴在Rt△QME中，，∴‎ 题型三 旋转变换 巩固练习 已知正方形中，点在边上，，（如图所示） 把线段绕 点旋转，使点落在直线上的点 第 13 页 共 14 页 处，则、两点的距离为 ．‎ 或．[来源:&中%国教育^出版~网@]‎ 题目里只说“旋转”，并没有说顺时针还是逆时针，而且说的是“直线上的点”，所以有两种情况如图所示：顺时针旋转得到点，则，逆时针旋转得到点，则，．‎ 在平面直角坐标系中，矩形的顶点、的坐标分别为和．将矩形 绕点顺时针旋转度，得到四边形，使得边与轴交于点，此时边、分别与边所在的直线相交于点、．‎ ‎⑴ 如图1，当点与点重合时，求点的坐标；‎ ‎⑵ 在⑴的条件下，求的值；‎ ‎⑶ 如图2，若点与点不重合，则的值是否发生变化？若不变，试证明你的结论；若有变化，请说明理由．‎ ‎（图1）‎ ‎（图2）‎ ‎（北京东城期末）‎ ‎[来源:z#zstep&.%^~com]‎ 第 13 页 共 14 页 ‎⑴ ∵将矩形绕点顺时针旋转度，得到四边形，[来源*:#中%国~教@育出版网]‎ 且、的坐标分别为和，‎ ‎∴，．‎ ‎（图1）‎ ‎∴．‎ ‎∴点的坐标为．[来@源:中国教育出&^*%版网]‎ ‎⑵ ∵，，‎ ‎∴．‎ ‎∵，且，‎ ‎∴．同理．[中国%#教&育出^版*网]‎ ‎∴，∴．[中^国教育~@出*版网#]‎ ‎（或：∵．∴．）‎ ‎⑶ 如图2所示，作交于点，‎ ‎∵，且，‎ ‎∴四边形是平行四边形．‎ ‎（图2）‎ ‎∴．‎ ‎∵，‎ ‎∴．‎ ‎∴．‎ 又∵，‎ ‎∴．‎ ‎∴．‎ 第 13 页 共 14 页 ‎∴的值不会发生改变．‎ 课后测 ‎【测试1】在四边形中，，，和的长度分别为和，那么的长为________．‎ ‎【解析】自点作交于，‎ 则四边形是平行四边形，，．又．‎ 所以，是等腰三角形．‎ ‎，[来源:%中@国教~育#出&版网]‎ 所以．‎ ‎【测试2】如图，已知中，，，点在边上，把沿翻折使与重合，得，则与重叠部分的面积为（　　）‎ A． B． C． D．‎ ‎【解析】A[来源:中@国教^育~出版*网%]‎ ‎[中国教育@出~^版*网&]‎ ‎【测试3】如图，正方形与正三角形的顶点重合，将绕顶点 第 13 页 共 14 页 旋转，在旋转过程中，当时，的大小可以是________．‎ ‎【解析】或 第 13 页 共 14 页