2019届中考数学 基础训练（2） 新版 苏科版

2019届中考数学 基础训练（2） 新版 苏科版

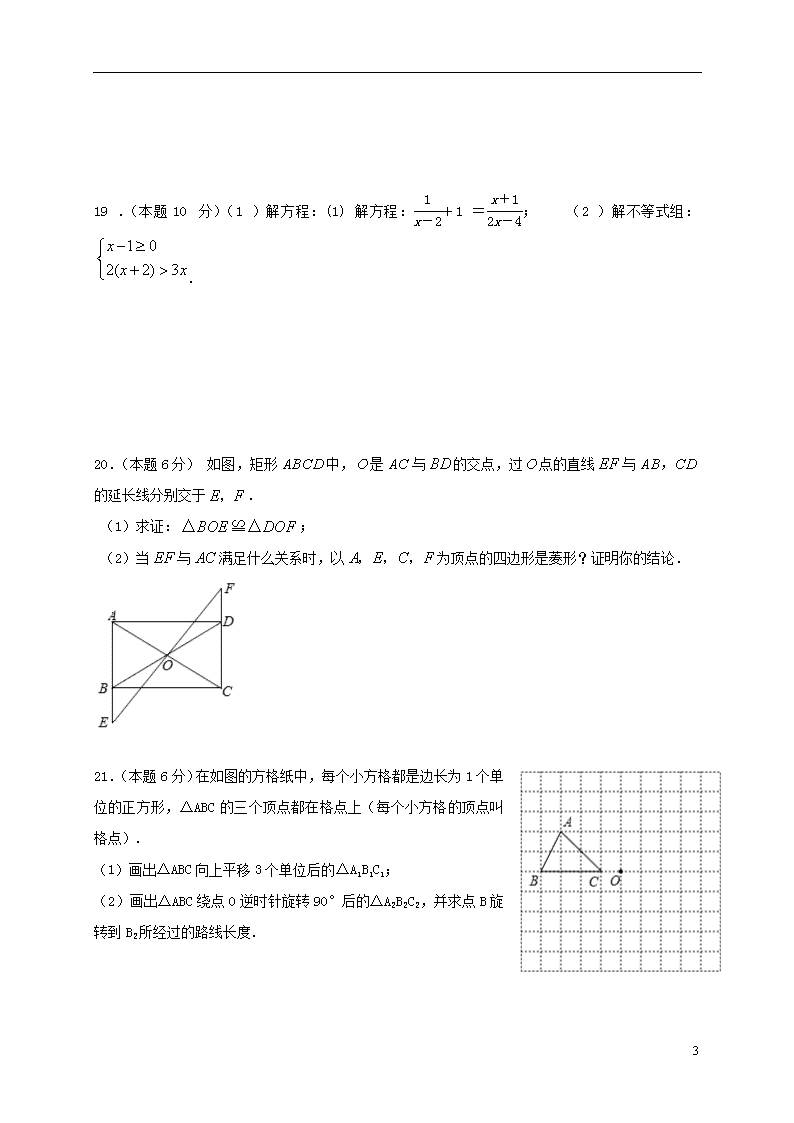
中考基础训练（2）‎ 一、填空题：（每小题2分，共24分）‎ ‎1．的相反数是 . 2． 函数中，自变量x的取值范围是 . ‎ ‎3．我们知道，1纳米=10—‎9米，一种花粉直径为35000纳米，那么这种花粉的直径用科学记数法可记为 米. ‎ ‎4．已知y是x的一次函数，下表列出了部分对应值，则m= . ‎ ‎5.如图，A、B、C为⊙0上三点，∠ACB＝20○,则∠BAO的度数为 °. ‎ ‎6. 如图，△ABC的外接圆的圆心坐标为　　　　　　　.‎ ‎7．如图，用一张长方形纸条折成一个图形，如果∠2=60°，那么∠1= °.‎ ‎8.若分式方程+=2无解，则m= .‎ ‎9．如图，用同样规格的黑白两色的正方形瓷砖铺设矩形地面，请观察图形并解答下列问题.在第n个图中，共有 白块瓷砖。（用含n的代数式表示）.‎ ‎10.在平面直角坐标系中，以点P（3，4）为圆心，r为半径的圆与两坐标轴恰有四个公共点，则r的值或范围是 .‎ ‎11．如图，在△ABC中，AC=BC=2，∠ACB=90°，D是BC边的中点，E是AB边上一动点，则EC+ED的最小值是 . ‎ ‎12．如图的平面直角坐标系中有一个正六边形ABCDEF，其中C．D的坐标分别为（1，0）和（2，0）．若在无滑动的情况下，将这个六边形沿着x轴向右滚动，则在滚动过程中，这个六边形的顶点A．B．C．D．E、F中，会过点（2013，2）的是点　 　．‎ 8‎ 二、选择题（每小题3分，共15分）‎ ‎13．下列运算正确的是 【 】‎ A． B． C． D ．‎ ‎14．若∠A的余角为60°，则sinA等于 【 】‎ ‎ A． B． C． D． ‎ ‎15．若一个圆锥的母线长是它底面圆半径的2倍，则它的侧面展开图的圆心角等于 【 】 ‎ A． B． C． D． ‎ ‎16．已知点A是双曲线在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为一边作等边三角形ABC，点C在第四象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式是 【 】‎ A．（x>0） B． （x>0） ‎ C． （x>0） D ．（x>0） ‎ ‎17．已知二次函数()的图象如图所示，有下列结论：①；②；③；④．其中，正确结论的个数是 【 】‎ A.1 B ‎.2 ‎C. 3 D. 4‎ 三、解答题（共计81分）‎ ‎18（本题8分）（1）计算：； （2）化简：.‎ 8‎ ‎ ‎ ‎ ‎ ‎19．（本题10分）（1）解方程：(1)解方程：＋1＝； （2）解不等式组：.‎ ‎20．（本题6分） 如图，矩形中，是与的交点，过点的直线与的延长线分别交于．‎ ‎（1）求证：；‎ ‎（2）当与满足什么关系时，以为顶点的四边形是菱形？证明你的结论．‎ ‎21．（本题6分）在如图的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点）.‎ ‎（1）画出△ABC向上平移3个单位后的△A1B‎1C1；‎ ‎（2）画出△ABC绕点O逆时针旋转90°后的△A2B‎2C2，并求点B旋转到B2所经过的路线长度.‎ 8‎ ‎22．（本题6分）某中学为促进课堂教学，提高教学质量，对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查．根据收回的问卷，学校绘制了“频数分布表”和“频数分布条形图”．请你根据图表中提供的信息，解答下列问题．‎ ‎（1）补全“频数分布表”；‎ ‎（2）在“频数分布条形图”中，将代号为“4”的部分补充完整；‎ ‎（3）四种方式中哪种教学方式喜欢的人最少？请你给老师的教学提一条有价值的建议. ‎ ‎23． (本题5分)小明骑自行车从家去学校，途经装有红、绿灯的三个路口．假没他在每个路口遇到红灯和绿灯的概率均为，则小明经过这三个路口时，恰有一次遇到绿灯的慨率是多少? 请用画树状图的方法加以说明．‎ 8‎ ‎24. (本题6分) 如图所示，A、B两地之间有一条河，原来从A地到B地需要经过桥DC，沿折线A→D→C→B到达，现在新建了桥EF，可直接沿直线AB从A地到达B地．已知BC=‎12km，∠A=45°，∠B=37°．桥DC和AB平行，则现在从A地到达B地可比原来少走多少路程？（结果精确到‎0.1km．参考数据：，sin37°≈0.60，cos37°≈0.80）‎ ‎25．(本题6分) 如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD.‎ ‎(1)求证:CD是⊙O的切线;‎ ‎(2)过点B作⊙O的切线交CD的延长线于点E,若CD=4,tan∠CDA= ,求BE的长.‎ 8‎ ‎26．（本题8分）某商场购进一批L型服装（数量足够多），进价为40元/件，以60元/件销售，每天销售20件。根据市场调研，若每件每降1元，则每天销售数量比原来多3件。现商场决定对L型服装开展降价促销活动，每件降价x元（x为正整数）。在促销期间，商场要想每天获得最大销售利润，每件降价多少元？每天最大销售毛利润为多少？（注：每件服装销售毛利润指每件服装的销售价与进货价的差）.‎ 答案 一、填空题（每题２分，共２４分）‎ ‎1. ； 2. ； 3. ； 4. 3 ； 5. 70°； 6. （6，2） ； ‎ ‎7. 120°； 8.1 ；　 9. n2+n ； 10. ； 11. ； 12. B 二、选择题 （每题３分，共１５分） ‎ ‎13. B 14 . A 15. D 16. C 17 . D 三、解答题 ‎18. （1）原式 　 ．．．．．．．．．．．．．．．．．．2分 ‎ ‎ = -2.5 ．．．．．．．．．．．．．．．．．．4分 　　　‎ ‎（2）原式= ．．．．．．．．．．．．．．．．．．6分 ‎ ‎ = ．．．．．．．．．．．．．．．．．．8分 ‎19．（1）解：2+2x－4=x+1 ．．．．．．．．．．．．．．．．．．2分 8‎ ‎ x=3 ．．．．．．．．．．．．．．．．．．3分 ‎ ‎ 经检验：当x=3时，，．．．．．．．．．．．．．．．．．．4分 所以x=3是原方程的解　　　　．．．．．．．．．．．．．．．．．．５分 ‎（2）解： ．．．．．．．．．．．．．．．．．．7分 ‎∴该不等式的解集为 1≤x＜4 ．．．．．．．．．．．．．．．．．．10分 ‎ ‎20．（1）略 ．．．．．．．．．．．．．．．．． 3分 ‎ （2）EF⊥AC 略 ．．．．．．．．．．．．．．．．． 3分 ‎　　　　‎ ‎21．（1）略　．．．．．．．．．２分 （2）画图 ．．．．．．．．４分 ．．．．．６分 ‎22、（1）频率 0.50 频数 50 ．．．．．． 2分 ‎（2）略 ．．．．．．．4分 ‎（3）答:代号1（老师讲，学生听）； ‎ 建议： 略 。 ．．．．．．．６分 ‎ ‎ 8‎ ‎23.‎ 画树状图 3分 P（一次绿色）= 5分 ‎24．辅助线-------------1分 ‎ 解出约5.4km． ．．．．．．．．．．6分 ‎25．（１）相切； ．．．．．3分 ‎（２）6　　　　　　　　　　　　　　　　　　．．．．．．．．．．．．．．．．．．6分 ‎ 26. 解：根据题意，商场每天的销售毛利润Z=（60－40－x）（20＋3x）=－3x2＋40x+400‎ ‎ ．．．．．3分 ‎ ∴当时，函数Z取得最大值。 ‎ ‎∵x为正整数，且， ．．．．．6分 ‎∴当x=7时，商场每天的销售毛利润最大，最大销售毛利润为－3·72＋40·7+400=533。 ．．．．．7分 答：商场要想每天获得最大销售利润，每件降价7元，每天最大销售毛利润为533元。．．．．8分 8‎