中考数学三大变换平移变换专训七学生用卷

中考数学三大变换平移变换专训七学生用卷

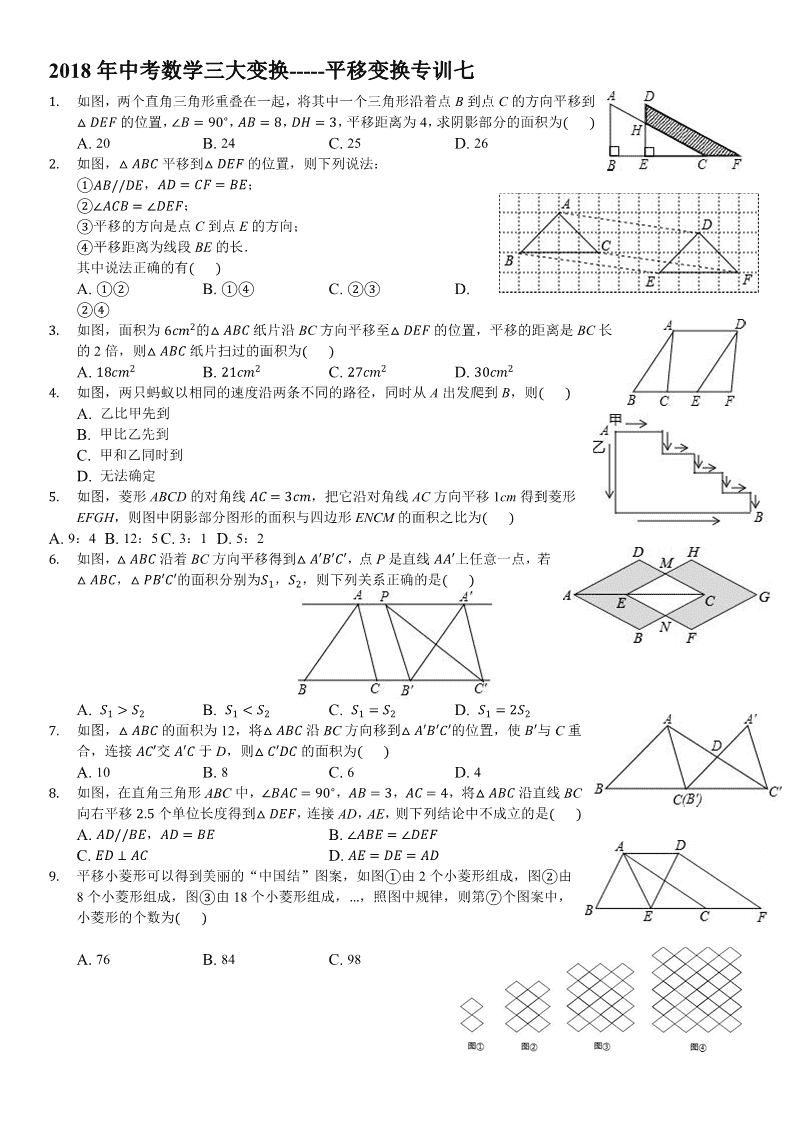
‎2018年中考数学三大变换-----平移变换专训七 1. 如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到‎△DEF的位置，‎∠B=‎‎90‎‎∘‎，AB=8‎，DH=3‎，平移距离为4，求阴影部分的面积为‎(‎　　‎‎)‎ A. 20 B. 24 C. 25 D. 26‎ 2. 如图，‎△ABC平移到‎△DEF的位置，则下列说法： ‎①AB//DE，AD=CF=BE； ‎②∠ACB=∠DEF； ‎③‎平移的方向是点C到点E的方向； ‎④‎平移距离为线段BE的长． 其中说法正确的有‎(‎　　‎‎)‎ A. ‎①②‎ B. ‎①④‎ C. ‎②③‎ D. ‎‎②④‎ 3. 如图，面积为‎6cm‎2‎的‎△ABC纸片沿BC方向平移至‎△DEF的位置，平移的距离是BC长的2倍，则‎△ABC纸片扫过的面积为‎(‎　　‎‎)‎ A. ‎18cm‎2‎ B. ‎21cm‎2‎ C. ‎27cm‎2‎ D. ‎‎30cm‎2‎ 4. 如图，两只蚂蚁以相同的速度沿两条不同的路径，同时从A出发爬到B，则‎(‎　　‎‎)‎ A. 乙比甲先到 B. 甲比乙先到 C. 甲和乙同时到 D. 无法确定 5. 如图，菱形ABCD的对角线AC=3cm，把它沿对角线AC方向平移1cm得到菱形EFGH，则图中阴影部分图形的面积与四边形ENCM的面积之比为‎(‎　　‎‎)‎ A. 9：4 B. 12：5 C. 3：1 D. 5：2‎ 6. 如图，‎△ABC沿着BC方向平移得到‎△A′B′C′‎，点P是直线AA′‎上任意一点，若‎△ABC，‎△PB′C′‎的面积分别为S‎1‎，S‎2‎，则下列关系正确的是‎(‎　　‎‎)‎ A. S‎1‎‎>‎S‎2‎ B. S‎1‎‎<‎S‎2‎ C. S‎1‎‎=‎S‎2‎ D. ‎S‎1‎‎=2‎S‎2‎ 7. 如图，‎△ABC的面积为12，将‎△ABC沿BC方向移到‎△A′B′C′‎的位置，使B′‎与C重合，连接AC′‎交A′C于D，则‎△C′DC的面积为‎(‎　　‎‎)‎ A. 10 B. 8 C. 6 D. 4‎ 8. 如图，在直角三角形ABC中，‎∠BAC=‎‎90‎‎∘‎，AB=3‎，AC=4‎，将‎△ABC沿直线BC向右平移‎2.5‎个单位长度得到‎△DEF，连接AD，AE，则下列结论中不成立的是‎(‎　　‎‎)‎ A. AD//BE，AD=BE B. ‎∠ABE=∠DEF C. ED⊥AC D. ‎AE=DE=AD 9. 平移小菱形可以得到美丽的“中国结”图案，如图‎①‎由2个小菱形组成，图‎②‎由8个小菱形组成，图‎③‎由18个小菱形组成，‎…‎，照图中规律，则第‎⑦‎个图案中，小菱形的个数为‎(‎　　‎)‎ ‎ A. 76 B. 84 C. 98 D. 102‎ 1. 如图，将‎△ABE向右平移2cm得到‎△DCF，如果‎△ABE的周长是16cm，那么四边形ABFD的周长是______ ． ‎ 2. 如图，AD是‎△ABC的中线，将‎△ABC沿射线BC方向平移2cm得到‎△EDF，则DC的长为______cm． ‎ 3. 如图，将边长为12的正方形ABCD沿其对角线AC剪开，再把‎△ABC沿着AD方向平移，得到‎△A′B′C′‎，当两个三角形重叠部分的面积为32时，它移动的距离AA′‎等于______ ．‎ 4. 如图，直角‎△ABC中，AC=3‎，BC=4‎，AB=5‎，则内部五个小直角三角形的周长为______．‎ 5. 如图，当半径为12cm的转动轮按顺时针方向转过‎150‎‎∘‎角时，传送带上的物体A平移的距离______cm． ‎ 6. 如图，将边长为3cm的正方形ABCD向上平移2个单位，再向右平移x个单位，重叠部分矩形周长为6，则x=‎ ______ ． ‎ 7. 如图，直线y=x−4‎与x轴、y轴分别交于M、N两点，‎⊙O的半径为2，将‎⊙O以每秒1个单位的速度向右作平移运动，当移动时间______ 秒时，直线MN恰好与圆相切．‎ 8. 如图所示，矩形ABCD的两条对角线相交于点O，AD=8‎，AB=6‎，将‎△ABO向右平移得到‎△DCE，则‎△ABO向右平移过程扫过的面积是______ ．‎ 9. 如图，‎△ABC中，AB=4‎，BC=6‎，‎∠B=‎‎60‎‎∘‎，将‎△ABC沿射线BC的方向平移，得到‎△A′B′C′‎，再将‎△A′B′C′‎绕点A′‎逆时针旋转一定角度后，点B′‎恰好与点C重合，则平移的距离为______ ，旋转角的度数为______ ．‎ 10. 如图，在边长为1个单位长度的小正方形组成的网格中，‎△ABC的位置如图所示‎(‎顶点是网格线的交点‎)‎ ‎(1)‎请画出‎△ABC向右平移2单位再向下平移3个单位的格点‎△‎A‎1‎B‎1‎C‎1‎； ‎(2)‎画出‎△ABC绕点O逆时针方向旋转‎90‎‎∘‎得到的‎△‎A‎2‎B‎2‎C‎2‎并求出旋转过程中点B到B‎2‎所经过的路径长． ‎ 1. 如图，将‎△ABC沿着射线BC方向平移至，使点落在‎∠ACB的外角平分线CD上，连结． ‎(1)‎判断四边形的形状，并说明理由； ‎(2)‎在‎△ABC中，‎∠B=‎‎90‎‎∘‎，AB=24‎，cos∠BAC=‎‎12‎‎13‎，求的长． ‎ 2. 如图，‎△ABC在直角坐标系中， ‎(1)‎请写出‎△ABC各点的坐标． ‎(2)‎若把‎△ABC向上平移2个单位，再向左平移1个单位得到‎△A′B′C′‎，写出 A′‎、B′‎、C′‎的坐标，并在图中画出平移后图形． ‎(3)‎求出三角形ABC的面积．‎ ‎ ‎ 3. 如图，在平面直角坐标系中，已知‎△ABC三个顶点的坐标分别是A(2,2)‎，B(4,0)‎，C(4,−4)‎． ‎(1)‎请在图中，画出‎△ABC向左平移6个单位长度后得到的‎△‎A‎1‎B‎1‎C‎1‎； ‎(2)‎以点O为位似中心，将‎△ABC缩小为原来的‎1‎‎2‎，得到‎△‎A‎2‎B‎2‎C‎2‎，请在图中y轴右侧，画出‎△‎A‎2‎B‎2‎C‎2‎，并求出‎∠‎A‎2‎B‎2‎C‎2‎的正弦值．‎ ‎ ‎