九年级数学中考复习二次函数实际应用利润问题教学设计

九年级数学中考复习二次函数实际应用利润问题教学设计

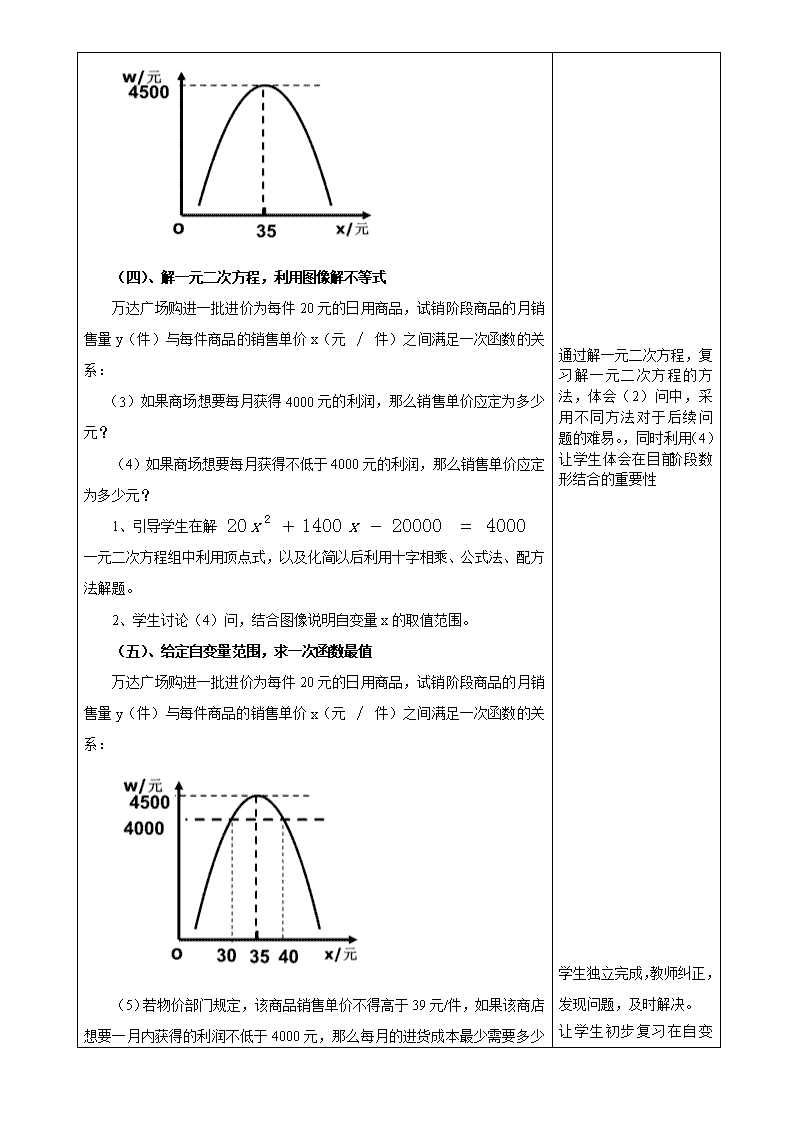
‎《《二次函数的实际应用—利润问题》教学设计 青岛第六十一中学 胡大海 教学目标 1．对本题的要求，通过实际问题背景考察学生构建数学模型，探究利用函数的图像与性质解决实际问题的能力，关注学生对变量间关系的刻画和数形结合的思想方法的运用，体现初、高中数学知识的衔接 ‎2. 利用所学的二次函数知识解决与利润相关的实际问题，发展学生应用数学解决问题的能力，是学生体会数学与生活的密切联系，并进一步感受数学的应用价值。‎ 重点 列函数关系式、二次函数的实际应用、利用二次函数求最值 难点 二次函数的实际应用、利用二次函数求最值 教学过程及设计思路：‎ 教学过程 设计思路 ‎（一）复习引入 ‎ 提问一次函数、二次函数相关知识以及一元二次方程的基本解法。‎ ‎（二）创设情境，列一次函数 万达广场购进一批进价为每件20元的日用商品，试销阶段每件商品的销售单价x（元 ∕ 件）与月销售量y（件）之间满足的关系如下如果月销售量是销售单价的一次函数。‎ x（元 ∕ 件）‎ ‎……‎ ‎30‎ ‎31‎ ‎32‎ ‎33‎ ‎34‎ ‎……‎ y（件）‎ ‎……‎ ‎400‎ ‎380‎ ‎360‎ ‎340‎ ‎320‎ ‎……‎ ‎（1）求y与x的函数关系式？‎ 学生审题思考，让学生回答以下三个问题：‎ ‎①x,y 各代表什么含义？‎ ‎②20代表什么含义？‎ ‎③y与x的是什么函数关系？‎ 学生口述解题思路，完成本题。‎ 变式（一）去掉“如果月销售量是销售单价的一次函数”，该如何求解，请同学口述解题思路。‎ 学生口述解题思路 变式（二）‎ 回顾所学函数的概念及类型，为解决二次函数实际应用利润问题学习提供知识储备。‎ 初步让学生感受二次函数实际应用中一次函数的数学模型 变式（一）、（二）、（三）。‎ 让学生感受一次函数不同的表示方式 万达广场购进一批进价为每件20元的日用商品，试销阶段商品的月销售量y（件）与每件商品的销售单价x（元 ∕ 件）之间满足的关系如图：‎ ‎30‎ ‎320‎ ‎400‎ ‎32‎ ‎（1）求y与x的函数关系式？‎ 学生思考后口述解题思路 变式（三）万达广场购进一批进价为每件20元的日用商品，试销阶段若以每件30元的价格销售，每月可以售出400件，经调查发现，如果单价每上涨2元，该商品每月的销量就减少40件。‎ ‎(1) 设每月获得销售量为y(件)，当销售单价为x（元），y与x的函数关系？‎ 学生思考后口述解题思路 ‎（三）、列二次函数关系式，并求最大值 万达广场购进一批进价为每件20元的日用商品，试销阶段商品的月销售量y（件）与每件商品的销售单价x（元 ∕ 件）之间满足一次函数的关系：‎ ‎ ‎ ‎(2)设每月获得利润为w(元)，当销售单价x定为多少元时，每月获得利润最大？最大利润是多少？‎ ‎1、从问题（2）中得出函数关系式为 ‎2、并引导学生利用三种方法求出最大利润：‎ ‎①化成顶点式。‎ ‎②利用顶点公式 ‎③求出顶点横坐标带入 ‎3、引导学生画出二次函数的草图。‎ 在第一问基础上，列出w与x的函数关系，并求出最大值，让学生感受二次函数在利润问题的应用，同时让学生初步体会求二次函数最大值的三种方法。复习二次函数草图画法。‎ ‎（四）、解一元二次方程，利用图像解不等式 万达广场购进一批进价为每件20元的日用商品，试销阶段商品的月销售量y（件）与每件商品的销售单价x（元 ∕ 件）之间满足一次函数的关系：‎ ‎（3）如果商场想要每月获得4000元的利润，那么销售单价应定为多少元？‎ ‎（4）如果商场想要每月获得不低于4000元的利润，那么销售单价应定为多少元？‎ ‎1、引导学生在解 一元二次方程组中利用顶点式，以及化简以后利用十字相乘、公式法、配方法解题。‎ ‎2、学生讨论（4）问，结合图像说明自变量x的取值范围。‎ ‎（五）、给定自变量范围，求一次函数最值 万达广场购进一批进价为每件20元的日用商品，试销阶段商品的月销售量y（件）与每件商品的销售单价x（元 ∕ 件）之间满足一次函数的关系：‎ 通过解一元二次方程，复习解一元二次方程的方法，体会（2）问中，采用不同方法对于后续问题的难易。，同时利用（4）让学生体会在目前阶段数形结合的重要性 学生独立完成，教师纠正，发现问题，及时解决。‎ ‎（5）若物价部门规定，该商品销售单价不得高于39元/件，如果该商店想要一月内获得的利润不低于4000元，那么每月的进货成本最少需要多少元？‎ 提问：进货成本怎么表示？‎ 销售单价不得高于39元/件，如果该商店想要一月内获得的利润不低于4000元能够求出什么？‎ 学生在讨论基础上口述解题思路，并完成。教师订正步骤。‎ ‎（六）、给定自变量范围，求二次函数最值 万达广场购进一批进价为每件20元的日用商品，试销阶段商品的月销售量y（件）与每件商品的销售单价x（元 ∕ 件）之间满足一次函数的关系： ‎ ‎（6）若物价部门规定，该商品销售单价不得高于39元/件，如果该商店每月的进货成本不超过5600元，那么售价定为多少元，每月获得的利润最大？最大利润是多少？‎ 提问：商品销售单价不得高于39元/件，如果该商店每月的进货成本不超过5600元能够求出什么？‎ 学生在讨论基础上口述解题思路，并完成。教师订正步骤。‎ 六、总结归纳 七、布置作业 让学生初步复习在自变量限制范围内，根据一次函数增减性确定函数因变量最值 学生独立完成，教师纠正，发现问题，及时解决。‎ 让学生初步复习在自变量限制范围内，根据二次函数增减性确定函数因变量最值