00053中考数学压轴题01

00053中考数学压轴题01

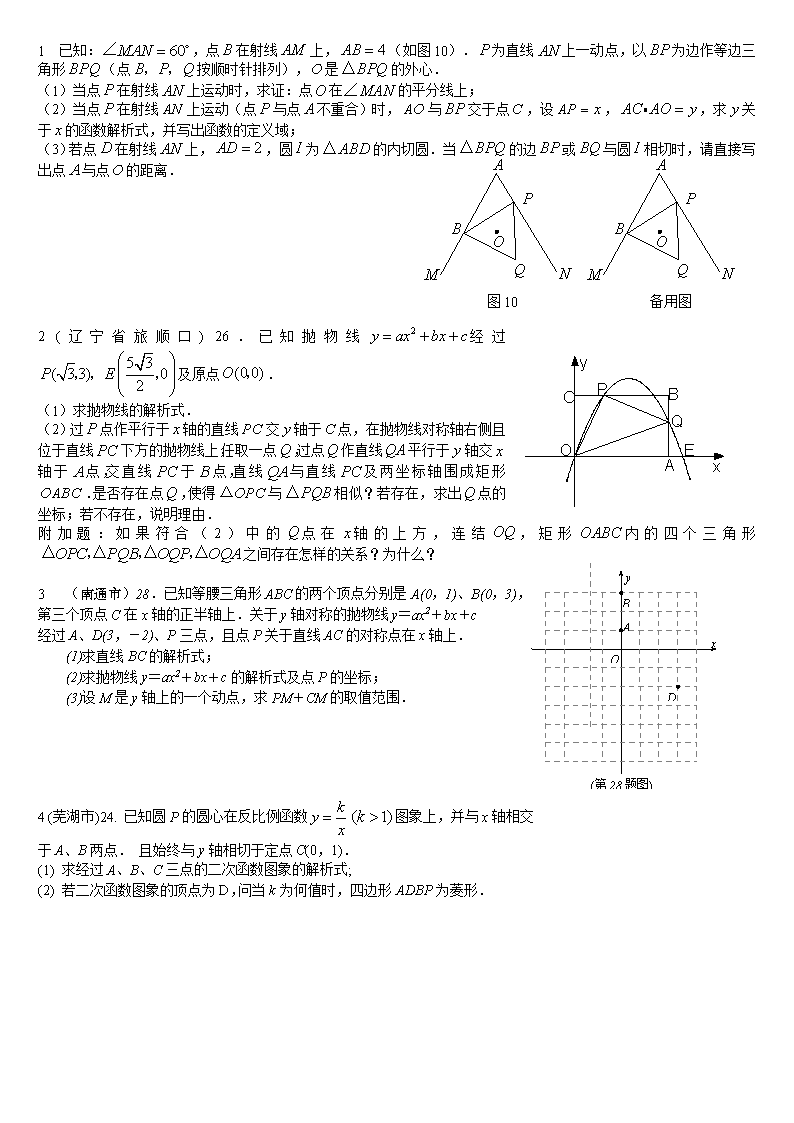
‎1 已知：，点在射线上，（如图10）．为直线上一动点，以为边作等边三角形（点按顺时针排列），是的外心．‎ ‎（1）当点在射线上运动时，求证：点在的平分线上；‎ ‎（2）当点在射线上运动（点与点不重合）时，与交于点，设，，求关于的函数解析式，并写出函数的定义域；‎ 图10‎ 备用图 ‎（3）若点在射线上，，圆为的内切圆．当的边或与圆相切时，请直接写出点与点的距离．‎ ‎2 (辽宁省旅顺口) 26．已知抛物线经过及原点．‎ ‎（1）求抛物线的解析式．‎ ‎（2）过点作平行于轴的直线交轴于点，在抛物线对称轴右侧且位于直线下方的抛物线上，任取一点，过点作直线平行于轴交轴于点，交直线于点，直线与直线及两坐标轴围成矩形．是否存在点，使得与相似？若存在，求出点的坐标；若不存在，说明理由．‎ A B O ‎(第28题图)‎ D x y 附加题：如果符合（2）中的点在轴的上方，连结，矩形内的四个三角形之间存在怎样的关系？为什么？‎ ‎3 （南通市）28．已知等腰三角形ABC的两个顶点分别是A(0，1)、B(0，3)，‎ 第三个顶点C在x轴的正半轴上．关于y轴对称的抛物线y＝ax2＋bx＋c 经过A、D(3，－2)、P三点，且点P关于直线AC的对称点在x轴上．‎ ‎(1)求直线BC的解析式；‎ ‎(2)求抛物线y＝ax2＋bx＋c的解析式及点P的坐标；‎ ‎(3)设M是y轴上的一个动点，求PM＋CM的取值范围．‎ ‎4 (芜湖市)24. 已知圆P的圆心在反比例函数图象上，并与x轴相交 于A、B两点． 且始终与y轴相切于定点C(0，1)．‎ (1) 求经过A、B、C三点的二次函数图象的解析式;‎ (2) 若二次函数图象的顶点为D，问当k为何值时，四边形ADBP为菱形．‎ ‎5 .(湖南省株洲市)25. 已知Rt△ABC，∠ACB＝90o，AC＝4，BC＝3，‎ CD⊥AB于点D，以D为坐标原点，CD所在直线为y轴建立如图所示平面直角坐标系.‎ ‎（1）求A、B、C三点的坐标；‎ ‎（2）若⊙O1、⊙O2分别为△ACD、△BCD的内切圆，‎ 求直线的解析式；‎ ‎（3）若直线分别交AC、BC于点M、N，判断CM与CN 的大小关系，并证明你的结论.‎ ‎6 （绵阳市）25.如图，已知抛物线y = ax2 + bx－3与x轴交于 A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心 M（1，m）恰好在此抛物线的对称轴上，⊙M的半径为．‎ 设⊙M与y轴交于D，抛物线的顶点为E．‎ ‎（1）求m的值及抛物线的解析式；‎ ‎（2）设∠DBC = a，∠CBE = b，求sin（a－b）的值；‎ ‎（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形 与△BCE相似？若存在，请指出点P的位置，并直接写出点P的坐标；‎ 若不存在，请说明理由．‎ ‎(第26题图)‎ A B C x O y l P P1‎ Q Q1‎ ‎7 (湖北省襄樊市非课改区)26. 如图，在平面直角坐标系中，以点 C(0，4)为圆心，半径为4的圆交y轴正半轴于点A，AB是⊙C的切线．‎ 动点P从点A开始沿AB方向以每秒1个单位长度的速度运动，点Q从O 点开始沿x轴正方向以每秒4个单位长度的速度运动，且动点P、Q从点A 和点O同时出发，设运动时间为t(秒)．‎ ‎(1)当t＝1时，得到P1、Q1两点，求经过A、P1、Q1三点的抛物线解析式 及对称轴l；‎ ‎(2)当t为何值时，直线PQ与⊙C相切？并写出此时点P和点Q的坐标；‎ ‎(3)在(2)的条件下，抛物线对称轴l上存在一点N，使NP＋NQ最小，求出点N的坐标并说明理由．‎ ‎2 解：（1）由已知可得：‎ ‎ ‎ 解之得，．‎ 因而得，抛物线的解析式为：．‎ ‎（2）存在．‎ 设点的坐标为，则，‎ 要使，则有，即 解之得，．‎ 当时，，即为点，所以得 要使，则有，即 解之得，，当时，即为点，‎ 当时，，所以得．‎ 故存在两个点使得与相似．‎ 点的坐标为．‎ 附加题：在中，因为．所以．‎ 当点的坐标为时，．‎ 所以．‎ 因此，都是直角三角形．‎ 又在中，因为．所以．‎ 即有．‎ 所以，‎ 又因为，‎ 所以．‎ ‎3 解：（1），，，‎ 是等腰三角形，且点在轴的正半轴上，，‎ ‎．．‎ 设直线的解析式为，，．‎ 直线的解析式为．‎ ‎（2）抛物线关于轴对称，．‎ y x A B D O ‎（第28题）‎ C P M Q 又抛物线经过，两点．‎ 解得 抛物线的解析式是．‎ 在中，，易得．‎ 在中，，，易得．‎ 是的角平分线．‎ 直线与轴关于直线对称．‎ 点关于直线的对称点在轴上，则符合条件的点就是直线与抛物线的交点．‎ 点在直线：上，‎ 故设点的坐标是．‎ 又点在抛物线上，‎ ‎．解得，．‎ 故所求的点的坐标是，．‎ ‎（3）要求的取值范围，可先求的最小值．‎ I）当点的坐标是时，点与点重合，故．‎ 显然的最小值就是点到轴的距离为，‎ 点是轴上的动点，无最大值，．‎ II）当点的坐标是时，由点关于轴的对称点，故只要求的最小值，显然线段最短．易求得．‎ 的最小值是6．‎ 同理没有最大值，的取值范围是．‎ 综上所述，当点的坐标是时，，‎ 当点的坐标是时， ．‎ ‎5 解: （1）在中，‎ M A D B N E C y x ‎ ‎ 同理 ‎（2）设的半径为的半径为，‎ 则有 ‎ 同理 ‎ 由此可求得直线的解析式为： ‎ ‎（3）与的大小关系是相等．‎ 证明如下：法一：由（1）易得直线的解析式为：，‎ 联立直线的解析式，求得点的纵坐标为，‎ 过点作轴于点，‎ ‎，由，得，‎ 解得： 同理，‎ 法二：由 由此可推理：‎ ‎6 解：（1）由题意可知C（0，－3），，‎ ‎∴ 抛物线的解析式为y = ax2－2ax－3（a＞0），‎ 过M作MN⊥y轴于N，连结CM，则MN = 1，，‎ ‎∴ CN = 2，于是m =－1．‎ 同理可求得B（3，0），‎ ‎∴ a×32－2－‎2a×3－3 = 0，得 a = 1，‎ ‎∴ 抛物线的解析式为y = x2－2x－3． ‎ ‎（2）由（1）得 A（－1，0），E（1，－4），D（0，1）．‎ ‎∴ 在Rt△BCE中，，，‎ ‎∴ ，，∴ ，即 ，‎ ‎∴ Rt△BOD∽Rt△BCE，得 ∠CBE =∠OBD =b，‎ 因此 sin（a－b）= sin（∠DBC－∠OBD）= sin∠OBC =．‎ ‎（3）显然 Rt△COA∽Rt△BCE，此时点P1（0，0）．‎ 过A作AP2⊥AC交y正半轴于P2，由Rt△CAP2 ∽Rt△BCE，得．‎ 过C作CP3⊥AC交x正半轴于P3，由Rt△P3CA∽Rt△BCE，得P3（9，0）．‎ 故在坐标轴上存在三个点P1（0，0），P2（0，1∕3），P3（9，0），使得以P、A、C为顶点的三角形与BCE相似．‎