2013年杭州市中考数学卷

2013年杭州市中考数学卷

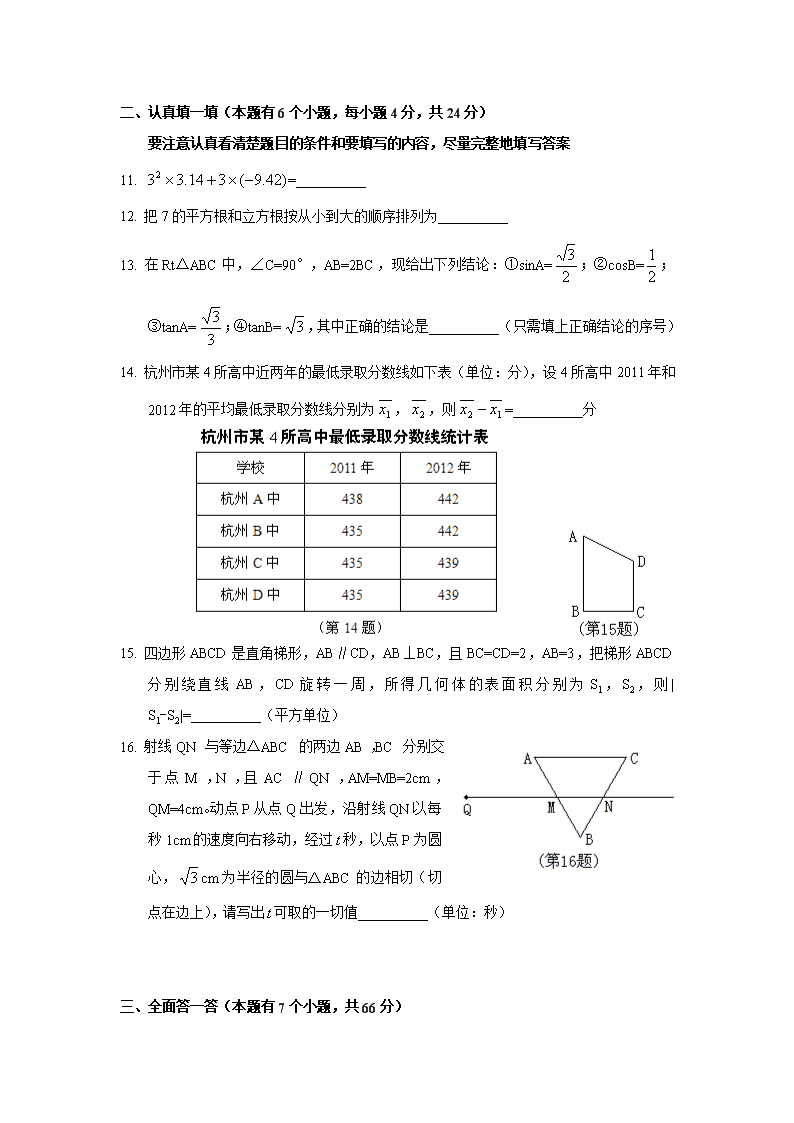
‎2013年杭州市各类高中招生文化考试 数 学 满分120分，考试时间100分钟 参考公式：‎ 直棱柱的体积公式：（S为底面积，为高）；‎ 圆锥的全面积（表面积）公式：（为底面半径，为母线长）；‎ 圆柱的全面积（表面积）公式：（为底面半径，为高）‎ 一、仔细选一选（本题有10个小题，每小题3分，共30分）‎ 下面每小题给出的四个选项中，只有一个是正确的。注意可以用多种不同的方法来选取正确答案。‎ ‎1. 下列“表情图”中，属于轴对称图形的是 ‎2. 下列计算正确的是 ‎ A. B. ‎ C. D. ‎ ‎3. 在□ABCD中，下列结论一定正确的是 A. AC⊥BD B. ∠A+∠B=180°‎ C. AB=AD D. ∠A≠∠C ‎4. 若，，则=‎ A. -10 B. ‎-40 C. 10 D. 40‎ ‎5. 根据2008~2012年杭州市实现地区生产总值（简称GDP，单位：亿元）统计图所提供的信息，下列判断正确的是 A. 2010~2012年杭州市每年GDP增长率相同 B. 2012年杭州市的GDP比2008年翻一番 C. 2010年杭州市的GDP未达到5500亿元 D. 2008~2012年杭州市的GDP逐年增长 ‎6. 如图，设（），则有 A. B. ‎ C. D. ‎ ‎7. 在一个圆中，给出下列命题，其中正确的是 A. 若圆心到两条直线的距离都等于圆的半径，则这两条直线不可能垂直 B. 若圆心到两条直线的距离都小于圆的半径，则这两条直线与圆一定有4个公共点 C. 若两条弦所在直线不平行，则这两条弦可能在圆内有公共点 D. 若两条弦平行，则这两条弦之间的距离一定小于圆的半径 ‎8. 如图是某几何体的三视图，则该几何体的体积是 A. B. ‎ C. D. ‎ ‎9. 在Rt△ABC中，∠C=90°，若AB=4，sinA=，则斜边上的高等于 A. B. C. D. ‎ ‎10. 给出下列命题及函数，和的图象 ‎①如果，那么；‎ ‎②如果，那么；‎ ‎③如果，那么；‎ ‎④如果时，那么。‎ 则 A. 正确的命题是①④ B. 错误的命题是②③④‎ C. 正确的命题是①② D. 错误的命题只有③‎ 二、认真填一填（本题有6个小题，每小题4分，共24分）‎ 要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案 ‎11. =__________‎ ‎12. 把7的平方根和立方根按从小到大的顺序排列为__________ ‎ ‎13. 在Rt△ABC中，∠C=90°，AB=2BC，现给出下列结论：①sinA=；②cosB=；③tanA=；④tanB=，其中正确的结论是__________（只需填上正确结论的序号）‎ ‎14. 杭州市某4所高中近两年的最低录取分数线如下表（单位：分），设4所高中2011年和2012年的平均最低录取分数线分别为，，则=__________分 ‎15. 四边形ABCD是直角梯形，AB∥CD，AB⊥BC，且BC=CD=2，AB=3，把梯形ABCD分别绕直线AB，CD旋转一周，所得几何体的表面积分别为S1，S2，则| S1-S2|=__________（平方单位）‎ ‎16. 射线QN与等边△ABC的两边AB，BC分别交于点M，N，且AC∥QN，AM=MB=‎2cm，QM=‎4cm。动点P从点Q出发，沿射线QN以每秒‎1cm的速度向右移动，经过秒，以点P为圆心，cm为半径的圆与△ABC的边相切（切点在边上），请写出可取的一切值__________（单位：秒）‎ 三、全面答一答（本题有7个小题，共66分）‎ 解答应写出文字说明，证明过程或推演步骤。如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以。‎ ‎17.（本小题满分6分）‎ 如图，四边形ABCD是矩形，用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q（不写作法，保留作图痕迹）。连结QD，在新图形中，你发现了什么？请写出一条。‎ ‎18.（本小题满分8分）‎ 当满足条件时，求出方程的根 ‎19.（本小题满分8分）‎ 如图，在等腰梯形ABCD中，AB∥DC，线段AG，BG分别交CD于点E，F，DE=CF。‎ 求证：△GAB是等腰三角形。‎ ‎20.（本小题满分10分）‎ 已知抛物线与轴相交于点A，B（点A，B在原点O两侧），与轴相交于点C，且点A，C在一次函数的图象上，线段AB长为16，线段OC长为8，当随着的增大而减小时，求自变量的取值范围。‎ ‎21.（本小题满分10分）‎ 某班有50位学生，每位学生都有一个序号，将50张编有学生序号（从1号到50号）的卡片（除序号不同外其它均相同打乱顺序重新排列，从中任意抽取1张卡片 ‎（1）在序号中，是20的倍数的有：20，40，能整除20的有：1，2，4，5，10（为了不重复计数，20只计一次），求取到的卡片上序号是20的倍数或能整除20的概率 ‎（2）若规定：取到的卡片上序号是（是满足1≤≤50的整数），则序号是的倍数或能整除（不重复计数）的学生能参加某项活动，这一规定是否公平？请说明理由；‎ ‎（3）请你设计一个规定，能公平地选出10位学生参加某项活动，并说明你的规定是符合要求的。‎ ‎22.（本小题满分12分）‎ ‎（1）先求解下列两题：‎ ‎①如图①，点B，D在射线AM上，点C，E在射线AN上，且AB=BC=CD=DE，已知∠EDM=84°，求∠A的度数；‎ ‎②如图②，在直角坐标系中，点A在轴正半轴上，AC∥轴，点B，C的横坐标都是3，且BC=2，点D在AC上，且横坐标为1，若反比例函数的图象经过点B，D，求的值。‎ ‎（2）解题后，你发现以上两小题有什么共同点？请简单地写出。‎ ‎23.（本小题满分12分）‎ 如图，已知正方形ABCD的边长为4，对称中心为点P，点F为BC边上一个动点，点E在AB边上，且满足条件∠EPF=45°，图中两块阴影部分图形关于直线AC成轴对称，设它们的面积和为S1。‎ ‎（1）求证：∠APE=∠CFP；‎ ‎（2）设四边形CMPF的面积为S2，CF=，。‎ ‎①求关于的函数解析式和自变量的取值范围，并求出的最大值； ‎ ‎②当图中两块阴影部分图形关于点P成中心对称时，求的值。‎