最新中考数学模拟试卷
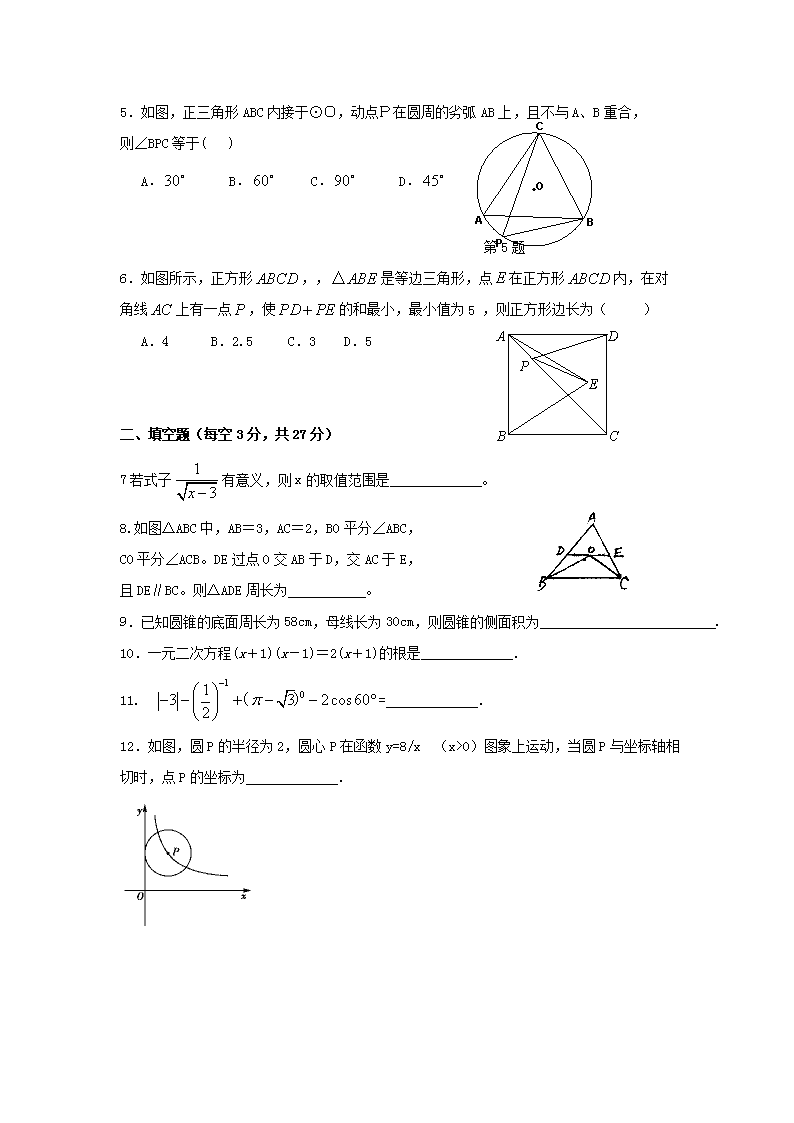
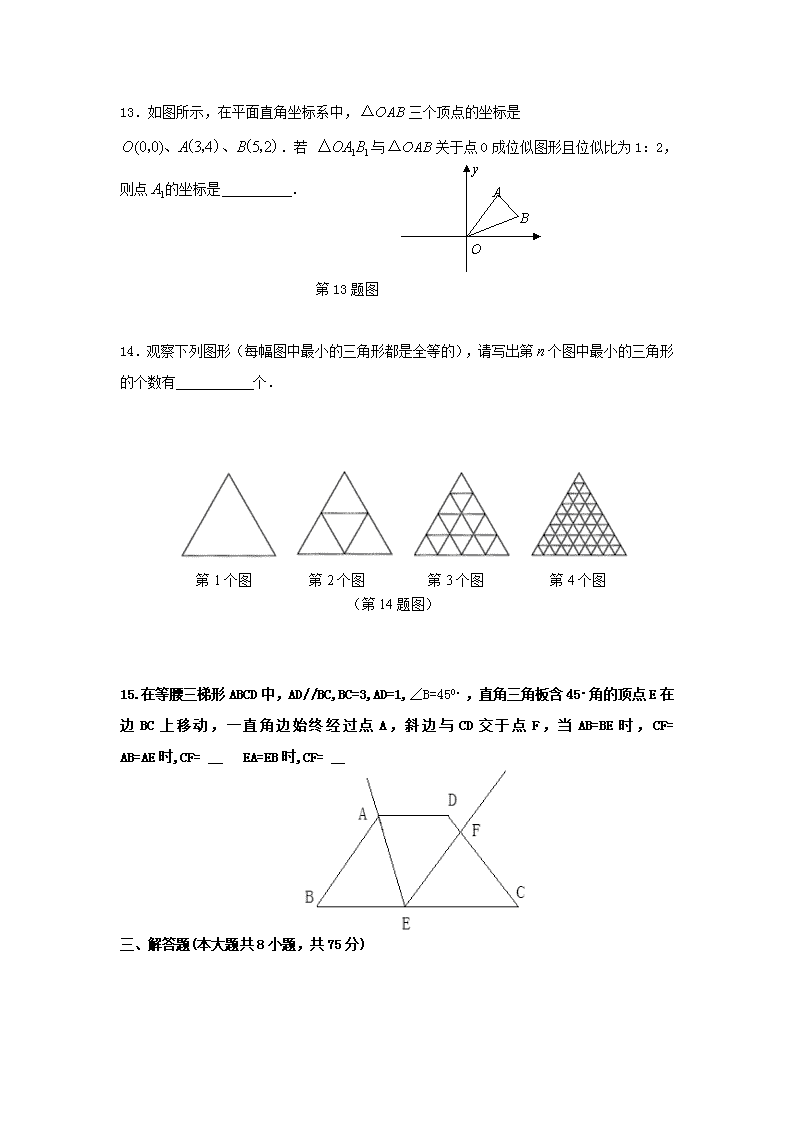
2011年最新中考数学模拟试卷（51）
温馨提示：
1． 本试卷共三道大题，23个小题。满分120分，考试时间100分钟．
2． 请用钢笔或圆珠笔直接答在试卷上。
3. 如缺页，考生须声明。
一、选择题（每小题3分，共18分）
下列各小题均有四个答案，其中只有一个正确答案，请把正确答案写在题后的括号内
1．下列计算中，正确的是（ ）
A． B．
C． D．
2．漯河市高度重视科技创新工作，全市科技投入从“十一五”初期的3.01亿元，增加到2010年的6.48亿元．请将6.48亿用科学记数法（保留两个有效数字）记为（ ）
A． B． C． D．
3.京剧是我国的国粹，剪纸是流传已久的民间艺术，这两者的结合无疑是最能代表中国特色的艺术形式之一．图中京剧脸谱剪纸中是轴对称图形的个数是（ ）
A．1个 B．2个 C．3个 D．4个
4．如图是由七个相同的小正方体堆成的物体，这个物体的俯视图是（ ）A． B． C． D．
5．如图，正三角形ABC内接于⊙Ｏ，动点Ｐ在圆周的劣弧AB上，且不与A、B重合，则∠BPC等于( )
A． B． C． D．
第5题
A
D
E
P
B
C
6．如图所示，正方形，，是等边三角形，点在正方形内，在对角线上有一点，使的和最小，最小值为5 ，则正方形边长为（ ）
A．4 B．2.5 C．3 D．5
二、填空题（每空3分，共27分）
7若式子有意义，则x的取值范围是 。
8.如图△ABC中，AB＝3，AC＝2，BO平分∠ABC，
CO平分∠ACB。DE过点O交AB于D，交AC于E，
且DE∥BC。则△ADE周长为 。
9．已知圆锥的底面周长为58cm，母线长为30cm，则圆锥的侧面积为 .
10．一元二次方程(x＋1)(x－1)＝2(x＋1)的根是 ．
11. = ．
12．如图，圆P的半径为2，圆心P在函数y=8/x （x>0）图象上运动，当圆P与坐标轴相切时，点P的坐标为 ．
Ob
Bb
Ab
yb
13．如图所示，在平面直角坐标系中，三个顶点的坐标是．若 与关于点O成位似图形且位似比为1：2，则点的坐标是 ．
第13题图
14．观察下列图形（每幅图中最小的三角形都是全等的），请写出第个图中最小的三角形的个数有 个．
第1个图
第2个图
第3个图
第4个图
（第14题图）
15.在等腰三梯形ABCD中，AD//BC,BC=3,AD=1, ∠B=450。 ，直角三角板含45。角的顶点E在边BC上移动，一直角边始终经过点A，斜边与CD交于点F，当AB=BE时，CF= AB=AE时,CF= EA=EB时,CF=
三、解答题(本大题共8小题，共75分)
16.（本小题6分）解分式方程：
17．（本小题8分）如图在RT△OAB中，∠OAB=90 º，OA=AB=6cm，将△AOB绕点O沿逆时针方向旋转
90 º得到△A1OB1 .
(1)线段O A1的长是 ，∠AOB1= 。
(2)连结AA1 ，求证四边形OAA1B1是平行四边形。
（3）求四边形OAA1B1的面积。
18. （本小题9分）在北半球某地有一间房子面向正南，假定房檐离地面BD=3m，
窗台高CD80cm，如果冬天太阳最低时，正午阳光光线与水平面的交点是32º，夏天太阳最高时，正午阳光光线与水平面的交角
是角76º，如果你是一名建筑师，请你帮忙设计房檐多宽，才能
正好在夏天使阳光进不了房子，而在冬天让太阳光线最大可能
地照进屋里？并计算冬天可照进屋里的最大深度。（参考数据：
Sin32º≈0.53, COS32º≈0.85,tan32º≈0.63
Sin58º≈0.85, COS58º≈0.53,tan58º≈1.60
Sin14º≈0.24,COS14º≈097,tan14º≈0.25，结果保留小数点后一位）
19．（本小题10分）为了美化我市，绿化环境，某中学七年级一班同学都积极参加了植树活动，今年四月该班同学的植树情况部分统计图如下图所示：
（1）请你根据以上统计图中的信息，填写下表：
该班人数
植树株数的中位数
植树株数的众数
（2）请你将扇形统计图和条形统计图补充完整。
（3）求从该班参加植树的学生中任意抽取一名，其植树株数超过该班植树株数的平均数的概率。
20．（本小题8分）早晨小娟与妈妈同时从家里出发，步行与自行车向相反方向的两地上学与上班，如图是他们离家的路程（米）与时间（分钟）之间的函数图象，妈妈骑车走了10分钟时接到小娟的电话，立即以原速度返回并前往学校，若已知小娟步行的速度为50米/分钟，并且妈妈与小娟同时到达学校，则小娟早晨上学需要的时间是多少，小娟家与学校的距离是多少？
21．（10分）如图，正方形ABCD中，E是AD边上一点，且BE=CE，BE与对角线AC交于点F，连接DF，交EC于点G．
（1）求证：∠ABF =∠ADF；
（2）求证：DF⊥EC．
22．(本小题10分）某人在再就业中心的扶持下，创办了“亦杨”报刊零售点，对经营的某种晚报，并提供了如下信息：
① 买进每份0．3元，卖出每份0．5元；
② 一个月内（以30天计），有20天每天可以卖出200份，其余10天每天只能卖出120份；
③ 一个月内，每天从报社买进的报纸份数必须相同，当天卖不掉的报纸以每份0.2元退回给报社：
（1）填表：
一个月内每天买进该种晚报的份数
100
150
当月利润（单位:元）
（2）设每天从报社买进该种晚报x份（120≤x≤200）时，月利润为y元，试求出y于x的函数关系式，并求月利润的最大值．
23．(本小题14分）已知：如图所示，关于的抛物线与轴交于点、点，与轴交于点．
（1）求出此抛物线的解析式，并写出顶点坐标；
（2）在抛物线上有一点，使四边形为等腰梯形，写出点的坐标，并求出直线的解析式；
B
A
O
C
y
x
（第23题图）
（3）在（2）中的直线交抛物线的对称轴于点，抛物线上有一动点，轴上有一动点．是否存在以为顶点的平行四边形？如果存在，请直接写出点的坐标；如果不存在，请说明理由．
2011年最新中考数学模拟试卷（51）
参考答案：
一、选择题(本大题有6小题，每小题3分，共18分)
题号
1
2
3
4
5
6
选项
C
D
C
C
B
D
二、填空题(本大题有9小题，每小题3分，共27分)
7. ＞3 8. 5 9. 870cm2 10. 11. 1
12. (2,4)(4,2) 13. (,-2)( ,2) 14. 4n-1 15 1
三、解答题(本大题有9小题，共75分)
16.解：1=2（X-3）-X （ 2分）
1=2X-6-X （3分）
X=7 （4分）
检验：把 X=7代入X-3 不等于0 （5分）
则X=7是原分式方程的解 （ 6分）
17．（1）6cm2 1350（一空1分）
(2)证明：由旋转900可知：∠A1OA=900
∠OA1B1= ∠OAB= 900
∴ A1B1 ∥OA
又∵A1B1 = OA
四边形OAA1B1是平行四边形 （3分）
（3）（3分）四边形的面积为18 cm2
18．(1)如图：中，∠ACB=140, （1分）
(3-0.8) 0.25 ≈ 0.6（米） （3分）
当房檐约0。6米时正好夏天使阳光进不了房子，冬天光线也很大 （4分）
设AE。BD交于点F ，则∠BAE=∠E=320 （5分）
，BF =O。60 ≈ 0.6 × O.63 ≈
O.38（ 米 ） （6分）
DF =3-O。38=2。62（ 米 ）
中 ， ∠ EBD=582 （7分）
ED =2。62× ≈2．62 ×1．60 ≈ 4.2 （米） （9分）
19．(1)50 3 2 （各一分） (2)图略 （4分） （3）0．5（3分）
20解：设妈妈追上小娟用了x分钟,则 （1分）
（250-50）x=2500+500 （4分）
x=15 （5分）
1. 15+10=25（分钟） （6分）
25+50=1250（米） （7分）
答：小娟早晨上学需要25分钟，小娟家离学校距离1250米 （8分）
21．（1）证明：∵四边形ABCD为正方形
∠BAC= ∠DAC AB = AD
又 ∵ AF = AF
≌
∠ADF=∠ABF （5分）
（2）证明： 和 中，
BE =CE
AB =CD
≌
∠AEB= ∠DEC
由（1）知
∠ABE= ∠ADF
∠ABE+∠AEB=900
∠ADF+∠DEC=900
∠DGE=1800-900=900
（5分）
22．（1）600 840（一空2分） （ 4分）
（2）由题意
Y=0.2(20x+10 120)-0.2(x-120) 10 （ 3分）
=2x+480（120≤x≤200） （ 4分）
2大于0
Y随x增大而增大
当x=200时 ＞ （ 5分）
Y最大 值680元 （ 6分）
23．解：（1）根据题意，得
B
A
O
C
y
x
第26题图
Q4
Q3
Q1
Q2
P3
P1
P2
D
C
P4
1分
解得 3分
抛物线的解析式为 4分
顶点坐标是（2，4） 5分
（2） 6分
设直线的解析式为
直线经过点点
7分
8分
9分
（3）存在． 10分
11分
12分
13分
14分
2011年最新中考数学模拟试卷（52）
一、选择题（共12小题，每小题3分，共36分）
1．－5的相反数是
A． B． C．5 D．－5
2．函数中自变量x的取值范围是
A． B． C． D．
3.不等式组的解集表示在数轴上正确的是
4. 下列说法正确的是
A．一颗质地均匀的骰子已连续抛掷了2000次，其中，抛掷出5点的次数最少，则第2001 次一定抛掷出5点．
B．可能性很小的事件在一次实验中一定不会发生．
C．天气预报说明天下雨的概率是50％，意思是说明天将有一半时间在下雨．
D．抛掷一枚图钉，钉尖触地和钉尖朝上的概率不相等．
5． A
B
D
O
C
第6题图
玉树地震后，各界爱心如潮，4月20日 搜索“玉树捐款”获得约7940000条结果，其中7940000用科学记数法表示应为
A． 79.4×104 B． 79.4×105
C． 7.94×105 D． 7.94×106
6． 如图，四边形ABCD中，∠A＋∠B＝200°，∠ADC、
∠DCB的平分线相交于点O，则∠COD的度数是
A.80° B．90° C．100° D．110°
7.分别由5个大小相同的正方体组成的甲、乙两个几何体如图所示，它们的三视图中完全一致的是
甲
乙
第7题图
A．主视图 B．俯视图
C．左视图 D．三视图
8．若是一元二次方程x2－3x－4＝0的两个根，则的值是
A． B．3 C．—3 D．—4
9．正整数按如图所示的规律排列．则第10行，第11列的数字是
第一行
第二行
第三行
第四行
第五行
第一列
第二列
第三列
第四列
第五列
1
2
5
10
17
…
4
3
6
11
18
…
9
8
7
12
19
…
16
15
14
13
20
…
25
24
23
22
21
…
……
第9题图
O
A
B
C
D
第10题图
A．98 B．106 C．110 D．118
10．如图，⊙O的直径AB＝4，BC切⊙O于点B，OC平行于弦AD，
OC＝5，则AD的长为
A． B． C． D．
11．百步亭社区调查某组居民双休日的学习状况，采取了下列调查方式：a
:从一幢高层住宅楼中选取200名居民；b:从不同住宅楼中随机选取200名居民；c:选取该组内的200名在校学生．并将最合理的调查方式得到的数据制成扇形统计图和部分数据的频数分布直方图。以下结论：①上述调查方式最合理的是b；②在这次调查的200名居民中，在家学习的有60人；③估计该组2000名居民中双休日学习时间不少于4小时的人数是1420人；④小明的叔叔住在该组，那么双休日他去叔叔家时，正好叔叔不学习的概率是0.1．
图①
在图书馆等场所学习
30％
60％
10％
在家学习
不学习
0
2
4
6
8
36
24
16
14
10
50
6
图②
在图书馆等场所学习
在家学习
时间(小时)
人数(人)
其中正确的结论是
A．①③ B．②④ C．①③④． D．①②③④．
12．如图，Rt△ABC中，AC⊥BC，AD平分∠BAC交BC于点D，DE⊥AD交AB于点E，M为AE的中点，BF⊥BC交CM的延长线于点F，BD＝4，CD＝3．下列结论：①∠AED＝∠ADC；②＝；③AC·BE＝12；④3BF＝4AC，其中结论正确的个数有
A．1个 B．2个 C．3个 D．4个
二.填空题（共4小题，每小题3分，共12分）
13．计算：sin60°＝________，＝________， ＝_____________．
14．小明等五名同学四月份参加某次数学测验的成绩如下：100、100、x、x、80．已知这组数据的中位数和平均数相等，那么整数x的值为 ．
yY
xX
O
A
B
第15题图
15．如图，直线经过A（0，4）和B（－2，0）两点，则不等式组 的解集为 ．
第16题图
y
x
Oo
A
D
M
C
B
16．如图，A、M是反比例函数图象上的两点，过点M作直线MB∥x轴，交轴于点B；过点作直线轴交轴于点，交直线MB于点D．BM:DM＝8:9，当四边形OADM的面积为时，k＝ ．
三.解答下列各题
17.（本题6分）解方程：
18．（本题6分）先化简，再求值：，其中
19．（本题6分）如图，点E和点C在线段BF上，AB∥DE，AC∥DF，BC＝EF，求证：AB＝DE．
FC
D
A
B
C
ED
20．（本题7分）一布袋中放有红、黄、白、黑四种颜色的球各一个，它们除颜色外其他都一样，小菲从布袋中摸出一球后放回去摇匀，再摸出一个球，请你利用列举法（列表或画树状图）分析并求出小菲两次都能摸到同色球的概率．
21.（本题7分）已知每个网格中小正方形的边长都是1，图中的图案是由三段以格点（每个小正方形的顶点叫格点）为圆心，半径分别为1、2、3的圆弧围成．
（1）填空：图中三段圆弧所围成的封闭图形的面积是 （结果保留）；
（2）请你在图中以（1）中的图为基本图案，借助轴对称变换和旋转变换设计一个完整的图案．
22．如图，△ABC内接于⊙O，AB是⊙O的直径，CD平分∠ACB交⊙O于点D，交AB于点F，弦AE⊥CD于点H，连接CE、OH．
（1）求证：△ACE∽△CFB；
（2）若AC＝6，BC＝4，求OH的长．
23．（本题10分）某商品的进价为每件40元，售价每件不低于50元且不高于80元．售价为每件60元时，每个月可卖出100件；如果每件商品的售价每上涨1元，则每个月少卖2件．如果每件商品的售价每降价1元，则每个月多卖1件．设每件商品的售价为元（为正整数），每个月的销售利润为元．
（1）求与的函数关系式并直接写出自变量的取值范围；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
（3）当每件商品的售价高于60元时，定价为多少元使得每个月的利润恰为2250元？
24．（本题10分）如图，已知点D为等腰直角△ABC内一点，∠CAD＝∠CBD＝15°．
（1）求证：AD＝BD；
（2）E为AD延长线上的一点，且CE＝CA，求证：AD+CD＝DE；
（3）当BD＝2时，AC的长为______．（直接填出结果，不要求写过程）
DC
ED
A
B
C
25. （本题12分） 在平面直角坐标系xOy中，已知抛物线与x轴交于A、B两点（点A在点B的左侧），交y轴的正半轴于点C，其顶点为M，MH⊥x轴于点H，MA交y轴于点N，sin∠MOH＝.
（1）求此抛物线的函数表达式；
（2）过H的直线与y轴相交于点P，过O，M两点作直线PH的垂线，垂足分别为E，F，若 ＝时，求点P的坐标；
（3）将（1）中的抛物线沿y轴折叠，使点A落在点D处，连接MD，Q为（1）中的抛物线上的一动点，直线NQ交x轴于点G，当Q点在抛物线上运动时，是否存在点Q，使△ANG 与△ADM相似？若存在，求出所有符合条件的直线QG的解析式；若不存在，请说明理由．
y
x
O
HC
ND
A
B
C
MD
2011年最新中考数学模拟试卷（52）
参考答案：
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
C
B
A
D
D
C
C
B
C
B
C
C
；﹣9a6 ；3；
60或110
-2＜x≤-1
6
17.解：a＝1，b＝2，c＝﹣2．
b2－4ac＝22－4×1×（﹣2）＝4＋8＝12．
x＝． ∴ x＝．∴ x1＝，x2＝ ．
18. 解：原式＝＝ ＝2—x．
当时，原式＝．
19． 证明：∵AB∥DE，AC∥DF，∴∠B＝∠DEF，∠ACB＝∠F．
在△ABC和△DEF中，
∵
∴△ABC≌△DEF．
∴AB＝DE．
20．解：列表如下：
红
黄
白
黑
红
红，红
黄，红
白，红
黑，红
黄
红，黄
黄，黄
白，黄
黑，黄
白
红，白
黄，白
白，白
黑，白
黑
红，黑
黄，黑
白，黑
黑，黑
第一次摸球
第二次摸球
结果
红球
红球
黄球
白球
黑球
红，红
红，黄
红，白
红，黑
黄球
红球
黄球
白球
黑球
黄，红
黄，黄
黄，白
黄，黑
第一次摸球
第二次摸球
结果
白球
红球
黄球
白球
黑球
白，红
白，黄
白，白
白，黑
黑球
红球
黄球
白球
黑球
黑，红
黑，黄
黑，白
黑，黑
由表或图可知，共有16种可能的结果，其中小菲两次都能摸到同色球出现4次，
故P（小菲两次都能摸到白球）＝＝
21．解：（1）3—6；
[来源:Www.zk5u.com]
（2）答案不唯一，以下提供两种图案．
22．（1）证明：
∵AB是⊙O的直径， ∴∠ACB＝90°．
∵CD平分∠ACB，∴∠ACD＝∠FCB＝45°．
∵AE⊥CD，∴∠CAE＝45°＝∠FCB．
在△ACE与△BCF中，
∠CAE＝∠FCB，∠ E＝∠B，∴△ACE∽△CFB．
（2）解：延长AE、CB交于点M．
∵∠FCB＝45°，∠CHM＝90°，
∴∠M＝45°＝∠CAE．
∴HA＝HC＝HM，CM＝CA＝6．
∵CB＝4 ，∴BM＝2．
∵OA＝OB，∴OH＝BM＝1．
23． 解：（1）当50≤≤60时，；
当60＜≤80时，；
∴ （50≤≤60且为整数）
＝
（60＜≤80且为整数）
（2）当50≤≤60时，；
∵a＝-1＜0，且x的取值在对称轴的左侧，∴y随x的增大而增大，
∴当x＝60时，有最大值2000；
当60＜≤80时，；
∵a＝-2＜0，∴当＝75时，有最大值2450．
综上所述，每件商品的售价定为75元时，每个月可获得最大利润，最大的月利润是2450元．
（3）当60<≤80时，．
当y＝2250元时，，解得：
其中，x＝85不符合题意，舍去．
∴当每件商品的售价为65元时，每个月的利润恰为2250元．
24．（1）证明：∵AC＝BC，∠ACB＝90°，
∴∠CAB＝∠ABC＝45°．
∵∠CAD＝∠CBD＝15°，
∴∠BAD＝∠ABD＝30°．
MD
DC
ED
A
B
C
∴ AD＝BD．
（2） 证明：在DE上截取DM＝DC，连接CM．
∵AD＝BD，AC＝BC，DC＝DC，
∴△ACD≌△BCD，
∴∠ACD＝∠BCD＝ 45°．
∵∠CAD＝15°，
∴∠EDC＝60°．
∵DM＝DC，
∴△CMD是等边三角形．
∴∠CDA＝∠CME＝120°，
∵CE＝CA，
DC
A
B
C
H
∴∠E＝∠CAD．
∴△CAD≌△CEM，
∴ME＝AD．
∴DA+DC＝ME+MD＝DE．
即AD+CD＝DE．
（2） 延长CD交AB于点H．则CH⊥AB．
∵∠HBD＝30°，BD＝2，
∴BH＝BD·cos30°＝．
∴AC＝BC＝BH÷sin45°＝．
25解：（1）∵ M为抛物线的顶点，
∴M（2，c）．∴OH＝2，MH＝|c|．∵a<0，且抛物线与x轴有交点，∴c＞0，∴MH＝c．
∵sin∠MOH＝，∴．∴OM＝，∵，∴MH＝c＝4．∴M（2，4）．∴抛物线的函数表达式为：．
（2）如图1，∵OE⊥PH，MF⊥PH，MH⊥OH．
∴∠EHO＝∠FMH，∠OEH＝∠HFM．∴△OEH∽△HFM．
∴＝＝．∵＝，∴MF＝HF．
∴∠OHP＝∠FHM＝45°．∴OP＝OH＝2，∴P（0，2）．
如图2，同理可得，P（0，﹣2）．
y
x
O
HC
ND
A
B
P
MD
EA
FB
CPD
图1
y
x
O
HC
ND
A
B
C
MD
EA
FB
PCPD
图2
（3）∵A（-1，0），∴D（1，0）．
∵M（2，4），D（1，0），∴MD：．∵ON∥MH，∴△AON∽△AHM，∴，∴AN＝，ON＝，N（0，）．
如图3，若△ANG ∽ △AMD，可得NG∥MD，∴QG：．
如图4，若△ANG ∽ △ADM，可得，．
∴AG＝，∴G（，0），∴QG：；
综上所述，符合条件的所有直线QG的解析式为：或．
y
D
x
O
HC
ND
A
B
C
MD
QFB
GCPD
图4
图3
y
D
x
O
HC
ND
A
B
C
MD
QFB
GCPD
2011年最新中考数学模拟试卷（53）
（满分120分，考试时间120分钟）
一． 填空：（8╳3，=24，）
1．-5的绝对值是———————。
2．函数y=中自变量x的取值范围是————————————————。
3．地球上海洋面积约为361 000 000平方千米，用科学记数法可以表示为————————————
平方千米。
4．一位同学画出的如图所示的几何体的三视图如下，其中错误的是——————————（填序号）
（1）主视图 （2）左视图 （3）俯视图
5．若a,b,c是△ABC的三条边，且a:b:c=2:3:4,则a,b,c这三条边上的对应高之比为
6．方程 (m-1)x2+2mx+m+3=0 有两个不相等的实数根，则m的取值范围是 。
7．在4张小卡片上分别写有实数0、、0.05、3/8，从中任取一张卡片，抽到有理数的概率是———— 。
8．一个扇形的圆心角是600，半径是10cm，则此扇形对应的弧长是——————————————cm。
二．选择（8╳3，=24，）
请将你认为正确的选择支的代号填在下面的表格里：
题号
9
10
11
12
13
14
15
16
答案
9．下列运算正确的是
A.（X-1）2=X2-1 B.3x2•x3=3x5 C.=-3 D.(-X3)2=-X6
10.若a,b,c分别是△ABC的三个角的对边，且满足(a-b)2+∣b-c∣=0,则△ABC是
A．等腰钝角三角形 B.直角三角形
C. 等腰直角三角形 D.等边三角形
11．教练员对射击运动员赛前的5次训练成绩进行统计分析，要了解运动员成绩是否稳定，需要知道运动员这5次训练成绩的
A．平均数或中位数 B.方差 C.众数或频率 D.众数或中位数
12．下列结论中，正确的是
A．2‹2‹3 B.数轴上的每一个点都表示一个有理数
C．（-35）0=0 D.是无理数
13．如果自变量x增加时，直线y=kx+b (k≠0,b≠0)先后经过第二、三、四象限，那么
A．k>O,b>0 B．k>0,b
o D．k100，所以一定超过全校平均次数． …………………4分
（2）这个学生的跳绳成绩在该班是中位数，由4+13+19=36，所以中位数一定在100～120范围内． …………………………………………4分
（3）该班60秒跳绳成绩大于或等于100次的有：19+7+5+2=33（人），
……………………………………………………………………………10分
所以，从该班任选一人，跳绳成绩达到或超过校平均次数的概率为0.66． ………………………………………………………… 12分
A
C
D
E
B
O
（第26题图）
l
26.解（1）在△AOC中，AC=2，
∵ AO＝OC＝2，
∴ △AOC是等边三角形．………2分
∴ ∠AOC＝60°，
∴∠AEC＝30°．…………………4分
（2）证明：∵OC⊥l，BD⊥l．
∴ OC∥BD． ……………………6分
∴ ∠ABD＝∠AOC＝60°．
∵ AB为⊙O的直径，
∴ △AEB为直角三角形，∠EAB＝30°． …………………………8分
∴∠EAB＝∠AEC．
∴ 四边形OBEC 为平行四边形． …………………………………9分
又∵ OB＝OC＝2．
∴ 四边形OBEC是菱形． …………………………………………12分
27.解：（1）∵四边形ABCD和四边形AEFG是正方形
M
B
E
A
C
N
D
F
G
图（1）
H
∴AB=AD，AE=AG，∠BAD＝∠EAG＝90º
∴∠BAE＋∠EAD＝∠DAG＋∠EAD
∴∠BAE＝∠DAG
M
B
E
A
C
N
D
F
G
图（2）
H
∴△ BAE≌△DAG …………4分
（2）∠FCN＝45º …………5分
理由是：作FH⊥MN于H
∵∠AEF＝∠ABE＝90º
∴∠BAE +∠AEB＝90º，∠FEH+∠AEB＝90º
∴∠FEH＝∠BAE
又∵AE=EF，∠EHF＝∠EBA＝90º
∴△EFH≌△ABE …………8分
∴FH＝BE，EH＝AB＝BC，∴CH＝BE＝FH
∵∠FHC＝90º，∴∠FCH＝45º …………9分
（3）当点E由B向C运动时，∠FCN的大小总保持不变，…………10分
理由是：作FH⊥MN于H
由已知可得∠EAG＝∠BAD＝∠AEF＝90º
结合（1）（2）得∠FEH＝∠BAE＝∠DAG
又∵G在射线CD上
∠GDA＝∠EHF＝∠EBA＝90º
∴△EFH≌△GAD，△EFH∽△ABE ……12分[来源:中.考.资.源.网]
∴EH＝AD＝BC＝b，∴CH＝BE，
∴＝＝
∴在Rt△FEH中，tan∠FCN＝＝＝ …………14分
2011年最新中考数学模拟试卷（58）
B
A
C
D
第5题图
O
注意事项：
1．本试卷共6页．全卷满分150分．考试时间为120分钟．考生答题全部答在答题卡上，答在本试卷上无效．
2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上．
3．答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案．答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置答题一律无效．
第8题图
2
4
4
H
E
D
G
C
F
B
A
4．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．
一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．-2的倒数是
A．2 B． -2 C． D．
2．下列运算中正确的是
A． B． C． D．
3．在“上海世博” 工程施工建设中，使用了我国科研人员自主研制的强度为460000000帕的钢材，那么数据460000000用科学记数法表示为
A． B． C． D．
4．下列四副图案中，不是轴对称图形的是
A． B． C． D．
5．如图，矩形的两条对角线的一个交角为60 o，两条对角线的长度的和为20cm，则这个矩形的一条较短边的长度为
A．10cm B．8 cm C．6 cm D．5 cm
6．如图，量角器外缘上有A，B两点，所表示的读数分别是80°，50°，则∠ACB应为
A．15° B． 25° C．30° D．40°
7．小明正在玩飞镖游戏，如果小明将飞镖随意投中如图所示的正方体木框中，那么投中阴影部分的概率为
A． B． C． D．
第7题图
第6题图
O
8．如图，直线是菱形ABCD和矩形EFGH的对称轴，C点在EF边上，若菱形ABCD沿直线
从左向右匀速运动，运动到C在GH边上为止,在整个运动的过程中,菱形与矩形重叠部分的面积（S）与运动的路程（x）之间的函数关系的图象大致是
D
O
S
X
2
4
A
O
S
X
2
4
B
O
S
X
2
4
C
O
S
X
2
4
二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
9． 在函数中，自变量x的取值范围是 ▲ .
10．分解因式： ▲ .[来源:学.科.网]
11．写出一个解为1，－2的一元二次方程： ▲ .
12．某班学生理化生实验操作测试成绩的统计结果如下表：
成绩/分
3
4
5
6
7
8
9
10
人数
1
1
2
2
8
9
15
12
则这些学生成绩的众数为 ▲ ．
第17题图
13．如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=128°,则∠DBC的度数为 ▲ °.
第13题图
原价： 元
五一8折优惠，现价：160元
第14题图
14．五一节期间，佳明眼镜店开展优惠学生配镜的活动，某款式眼镜的广告如图，请你为广告牌补上原价： ▲ 元．
15．将点A（4，0）绕着原点顺时针方向旋转45°角得到点B，则点B的坐标关系式是
▲ ．
16．反比例函数 y＝ 的图象与正比例函数y＝3x的图象交于点P(m，6)，则反比例函数的关系式是 ▲ ．
M
O
P
N
B
A
第18题图
17．如图，一个空间几何体的主视图和左视图都是边长为1
的正三角形，俯视图是一个圆，那么这个几何体的侧面积
是 ▲ ．
18．如图，是⊙O的直径，，点在⊙O上，
，为弧AN的中点，是直径上
一动点，则的最小值为 ▲ .
三、解答题（本大题共有9小题，共96分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19． ①(6分)计算：．
．
②(6分)解不等式组：
20．(8分)先化简：再选择一个合适的数代入求值.
21．(8分)观看了60周年国庆阅兵大典后，我们知道：中国人民解放军由陆军、海军、空军、二炮四个兵种组成.现将四个兵咱的现役兵力情况绘制成如下扇形和条形统计图，请根据不完整的统计图提供的信息，解答下列问题：
（1）中国人民解放军现役兵力共 万人.
（2）在扇形统计图中, ,= .
（3）补全条形统计图.
第21题图
第22题图
A
B
C
D
E
F
22．(8分)矩形ABCD中，以点B为圆心、BC长为半径画弧，交AD边于点E，连接BE，过C点作CF⊥BE，垂足为F．猜想线段BF与图中现有的哪一条线段相等？
先将你猜想出的结论填写在下面的横线上，然后再加以证明．
结论：BF=_______________．
证明：
23． (10分)在物理试验中，当电流在一定时间段内正常通过电子元件“ ”时，每P
Q
a
b
个电子元件的状态有两种可能：通电或断开，并且这两种状态的可能性相等．
是 ▲ ．
图1
P
Q
（1）如图1，当只有一个电子元件时，之
图2
间电流通过的概率是 ．
P
Q
图3
（2）如图2，当有两个电子元件并联时，请你用树状图（或列表法）表示图中 之间电流能否通过的所有可能情况，求出之间电流通过的概率.
（3）如图3，当有三个电子元件并联时，请你猜想之间电流通过的概率是 ．
24．(12分)如图，在由边长为1的小正方形组成的网格中，的三个顶点均在格点上，请按要求完成下列问题：
（1）画AD∥BC（D为格点），连接CD；
（2）线段CD的长为 , AC的长为 ；
（3）请你在的三个内角中任选一个锐角，若
你所选的锐角是 ，则它所对应的正弦函数
第24题图
值是 ；
第24题图
（4）若E为BC中点，F为AD中点．则tan∠CAE的值是 ,四边形AECF的形状为 ， 面积为 ．
25．（12分）甲乙两人同时登山，甲、乙两人距地面的高度（米）与登山时间
（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：
（1）甲登山的速度是每分钟 米，乙在地提速时距地面的高度为 米．
（2）若乙提速后，乙的速度是甲登山速度的3倍，请分别求出甲、乙二人登山全过程
中，登山时距地面的高度（米）与登山时间（分）之间的函数关系式．
（3）登山多长时间时，乙追上了甲？此时乙距地的高度为多少米？
第25题图
26．(12分)为了加强视力保护意识，小明想在长为3.2m，宽为4.3m的书房里挂一张测试距离为5m的视力表．在一次课题学习课上，小明向全班同学征集“解决空间过小，如何放置视力表问题”的方案，其中甲、乙、丙三位同学设计方案新颖，构思巧妙．[来源:学,科,网]
①甲生的方案：如图1，将视力表挂在墙ABEF和墙ADGF的夹角处(视力表与墙角之间的距离忽略不计)，被测试人站立在对角线AC上．问：甲生的设计方案是否可行？请说明理由．
②乙生的方案：如图2，将视力表挂在墙CDGH上，在墙ABEF上挂一面足够大的平面镜，根据平面镜成像原理可计算得到：测试线应画在距离墙ABEF m处．
③丙生的方案：如图3，根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表．如果大视力表中“E”的长是3.5cm，那么小视力表中相应“E”的长是多少cm？
H
H
（图1）
（图2）
（图3）
3.5㎝
A
C
F
3m
B
5m
D
第26题图
27．（14分）已知抛物线（m为常数）经过点（0，4）.
（1）求m的值；
（2）将该抛物线先向右、再向下平移得到另一条抛物线.已知这条平移后的抛物线满足下述两个条件：它的对称轴（设为直线l2）与平移前的抛物线的对称轴（设为l1）关于y轴对称；它所对应的函数的最小值为－8.
①试求平移后的抛物线所对应的函数关系式；
②试问在平移后的抛物线上是否存在着点P，使得以3为半径的⊙P既与x轴相切，又与直线l2相交？若存在，请求出点P的坐标，并求出直线l2被⊙P所截得的弦AB的长度；若不存在，请说明理由.
2011年最新中考数学模拟试卷（58）
参考答案
1-8： DBCA DADD 9. 10. 11. 答案不唯一，如 12. 9分 13. 52° 14. 200元 15. 16. 17. ； 18.
说明：选择题和填空题每小题都是3分，共54分.
19.（1）解：原式= …………4分 （注：每个运算正确得1分）
= …………6分
（2）解：由①得： …………………………1分
由②得： …………………………4分
∴不等式组的解集为: …………………………6分
20．解：原式= …………2分
…………………………4分
= ……………………………6分
代入求值正确的给2分，共8分.(代入的数不能是2和1)
21．① 250 ； ② 17% ，70%； ③ 略.（每空2分，补全统计图2分，共8分）
22．BF=AE ………2分
证明：矩形ABCD中，AD∥BC，∴∠AEB=∠CBF且∠A=90°……………………4分
又CF⊥BE ∴∠CFB=∠A=90°.又∵半径BC=BE ……………………… 6分
∴△ABE≌△FCB ………………………………………………………… 7分
∴BF=AE ……………………………………………………………………8分
23．（1） …………………………………………………………2分
（2）用树状图表示是：
通电
断开
通电
断开
通电
断开
a
b
或用列表法表示为：
通电
断开
通电
（通电，通电）
（通电，断开）
断开
（断开，通电）
（断开，断开）
……………………6分
从上可以看到之间电流通过的概率是．……………………………… 8分
（3） ……………………………………………10分
24.①图略（图中只有一个符合条件的格点） ；…………………………………3分
②5，；……………………………………………………………………5分
③，或，；……8分（第一空1分，第二空2分）
④，菱形，5；………………………12分（第一、二空各1分，第二空2分）
25.（1）10，30……………………2分
（2）由图知： …………………3分
，∴线段的解析式：…………5分
，，∴折线的解析式为：…8分
（3）由解得………………………………………10分
∴登山6.5分钟时乙追上甲．此时乙距地高度为（米）.………12分
26．（1）甲生的设计方案可行．…………1分
根据勾股定理，得．………3分
∴．∴甲生的设计方案可行．………………5分
（2）米．…………………8分
（3）∵∥ ∴△∽△． ∴． ………10分
∴． ∴（）．
答：小视力表中相应“”的长是．…………………………12分
27．解：（1）依题意得：02+4×0 + = 4，解得= 4…………………………3分
（2）①由（1）得： ∴对称轴为直线:…4分
依题意平移后的抛物线的对称轴为直线:………………………5分
故设平移后的抛物线所对应的函数关系式为………6分
∵此函数最小值为－8，∴
即平移后的抛物线所对应的函数关系式为…7分
②存在. 理由如下： 由①知平移后的抛物线的对称轴为直线:
当点P在轴上方时，∵⊙P与轴相切，故令= 3，
解得= 2±…………………………………………………………………9分
此时点P1（2+，3），P2（2－，3）与直线= 2之距均为，
∵＞3，∴⊙P1、⊙P2均与直线:= 2相离.
故点P1、P2不合题意，应舍去. …………………………………………………10分
当点P在轴下方时，∵⊙P与x轴相切，故令= -3，
解得= 2±…………………………………………………………………11分
此时点P3（2+，－3），P4（2，－3）与直线x = 2之距均为，
∵＜3，∴⊙P3、⊙P4均与直线:x = 2相交,故点P3、P4符合题意. ……12分
此时弦
综上，点P的坐标为（2+，－3）或（2，－3）
直线被⊙P所截得的弦AB长为4. …………………………………………14分
（备注：全卷各题若有其他解法，只要正确请参照给分）
2011年最新中考数学模拟试卷（59）
得分
评卷人
（满分150分，答卷时间120分钟）
一、选择题：本大题共8小题；每小题3分，共24分。下列各题都有代号为A、B、C、D的四个结论供选择，其中只有一个结论是正确的。请将正确选项的代号填在左边的括号里。
【 】1．的值是
A．—6 B．6 C． D．9
【 】2．下列运算正确的是
A． B．
C． D．
【 】3．小华拿一个矩形木框在阳光下玩，矩形木框在地面上形成的投影不可能是
A B C D
【 】4．如图，在等边三角形中，为的中点，，则和（不包含）相似的三角形有（ ）
A．1个 B．2个 C．3个 D．4个
【 】5．如图，已知O是四边形ABCD内一点，OA=OB=OC，∠ABC =∠ADC =65°，
则∠DAO +∠DCO的度数是
A
O
D
C
B
A．130° B．230° C．262.5° D．165°
第4题图 第5题图
【 】6．实数在数轴上对应点的位置如图所示，则必有
A． B．
C． D．
时间（分钟）
o
路程
5
7
0
a
1
0
b
第6题图
第8题图
【 】7．已知某反比例函数的图象经过点，则它一定也经过点
A． B． C． D．
【 】8．一名考生步行前往考场，5分钟走了总路程的，估计步行不能准时到达，于是他改乘出租车赶往考场，他的行程与时间关系如图所示（假定总路程为1，出租车匀速），则他到达考场所花的时间比一直步行提前了
A．18分钟 Ｂ．20分钟 Ｃ．24分钟 D．28分钟
得分
评卷人
二、填空题：本题共10小题；每小题3分，共30分。不需要写解答过程，请把最后结果填在横线上。
9．写出一个大于的负无理数： .
10.截至2010年，南通市绿化总面积达到4103.7万平方米。这个数据用科学记数法表示为
_________________平方米.
11.二次函数取得最大值时，= ．
12.将点M向左平移3个单位，再向下平移2个单位得到M′(—2,—3),则点M的坐标
是 ．
13.若等腰三角形的一个外角为150°，则它的底角为 度．
主视图
左视图
2
2
5
3
14.数学家发明了一个魔术盒，当任意实数对进入其中时，会得到一个新的实数：．例如把放入其中，就会得到．现将实数对（）放入其中得到实数4，则= ．
15.如图，长方体的主视图和左视图如图所示
（单位：cm）,则其俯视图的面积为 cm2．
第15题图
B
O
B1
y
C1
B4
B3
B2
C3
C2
C
x
16.在中，边不动，改变点的位置，使得减少度，增加度， 增加度，则三者之间的等量关系是 ．
A
C
B
45°
第17题图 第18题图
17.如图，，，要使惟一确定，那么的长度满足的条件是 ．
18.如图，点O (0,0)，B (0,1)是正方形OBB1C的两个顶点，以对角线OB1为一边作正方形OB1B2C1，再以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2……，依次下去，则点B7的坐标是 ．
得分
评卷人
三、解答题：本大题共10小题，共96分。解答时应写出文字说明、证明过程或演算步骤。
19．（本题6分）计算：
20．（本题8分）先化简：，再取一个你喜爱的的值代入求值．
得分
评卷人
21．（本题8分）解不等式组并把解集在数轴上表示出来．
22．（本题9分）已知直线及外一点，分别按下列要求画图，并写出画法，保留作图痕迹．
（1）在图1中，只用圆规在直线上画出两点，使得点
是一个等腰三角形的三个顶点；
（2）在图2中，只用圆规在直线外画出一点，使得点所在直线与直线平行．
Ａ
l
图1
Ａ
l
图2
得分
评卷人
23．（本题9分）如图，已知在平面直角坐标系中，平行四边形顶点，，直线将平行四边形分成面积相等的两部分，求的值．
关注50%
一般
15%
不关心
%
A、B、C三个小区共计
50
100
150
人数
态度
关注
一般
不关心
24．（本题10分）随着科学发展观的深入贯彻落实和环境保护、节能减排以及生态文明建设的全面推进，公众环境意识有了普遍提高。3月的某一天，小明和小刚在本市的A、B、C三个小区，对“低碳生活、节能减排”的态度，进行了一次随机调查．结果如下面的图表：
小区
态度
A
B
C
合计
关注
20
75
55
150
一般
23
17
不关心
57
20
28
105
（1）请将图表补充完整；
（2）此次共调查了多少人？
（3）用你所学过的统计知识来说明哪个小区的调查结果更能反映老百姓的态度．请写出一句关于倡导“节能减排”的宣传语。
得分
评卷人
A
B
M
北
东
S
W
25．（本题10分）如图，一艘船以每小时40海里的速度向西南方向航行，在A处观测灯塔M在船的南偏西75°的方向，航行9分钟后到达B处，这时灯塔M恰好在船的正西方向。已知距离此灯塔9海里以内的海区有暗礁，这艘船继续沿西南方向航行是否有触礁的危险？为什么？（参考数据：，）
26．（本题10分）一枚均匀的正方体骰子，六个面分别标有数字1、2、3、4、5、6，连续抛掷两次，朝上的数字分别为m、n，若把m、n作为点P的横、纵坐标，那么点P（）在函数的图像上的概率是多少？写出解答过程．
得分
评卷人
27．（本题12分）2010年5月1日，第41届世界博览会在上海市举行，本次世博会的主题是“城市，让生活更美好”（Better City, Better Life）。主办机构预计吸引世界各地7000万人次参观者前往，总投资达450亿人民币，是世界博览会史上最大规模．世博园某馆前有一块边长为8米的正方形花圃，如图AE=AF，点G、H、I分别是EF、CE、CF的中点，计划在△GHI内放置吉祥物“海宝”塑像，在阴影部分种植江苏荷花，其余部分种植广西茉莉。原来种植1平方米荷花和1平方米茉莉的总成本为200元，受季节和气候的影响，经核算荷花的种植成本提高了2成，茉莉的种植成本降低了1成，使每平方米荷花和每平方米茉莉的种植总成本提高了8%．
⑴试求出实际1平方米荷花和1平方米茉莉种植成本分别是多少元？
⑵若此花圃实际种植总成本为7956元，请求出AE的长度．
A
C
D
G
B
I
E
F
H
得分
评卷人
28．（本题14分）如图，在平面直角坐标系中，已知点B（）、
A（）（），以AB为边在x轴下方作正方形ABCD，点E是线段OD与正方形ABCD的外接圆的交点，连接BE与AD相交于点F．
(1)求证：BF=DO；
(2)若AE=DE
，试求经过B、F、O三点的抛物线l的解析式；
O
A
B
C
D
E
F
y
x
(3)在(2)的条件下，将抛物线l在x轴下方的部分沿x轴翻折，图像的其余部分保持不变，得到一个新图像，若直线BE向上平移t个单位与新图像有两个公共点，试求t的取值范围．
2011年最新中考数学模拟试卷（59）
答案
一、选择题(本大题共8小题；每小题3分，共24分)
题号
1
2
3
4
5
6
7
8
答案
C
B
A
C
D
D
A
B
二、填空题(本大题共10小题；每小题3分，共30分)
9．答案不唯一 10． 11． 12． 13．30或75 14．－1或3 15．15 16． 17． 或 18．
三、解答题（本大题共10小题，共96分）
19．（本题6分）解：原式＝…………………3分
＝…………………………5分
＝……………………………………6分
20．（本题8分）解：原式＝………………2分
＝…………………4分
＝
＝……………………………………6分
x的值不能为3、2、－2，过程略…………………………………………8分
21．（本题8分）解：
…………………①
…………………②
由①得： …………………………………………………………2分
由②得：
……………………………………………4分
∴不等式组的解集为…………………………………………6分
用数轴表示如下：
-3 -2 -1 0 1 2 3
…………………8分
22．（本题9分）解：（1）本题有2种画法，画对其中1种即可。
画法一：以点为圆心，大于点到直线的距离长为半径画弧，与直线交于两点，则点即为所求．…………………………………1分
画图正确．……………………………………………………………………3分
画法二：在直线上任取一点，以点为圆心，长为半径画弧，与直线交于点，则点即为所求．…………………………………………………………………………1分
画图正确．……………………………………………………………………3分
（2）画法：
在直线上任取两点，以点为圆心，长为半径画弧，以点为圆心，长为半径画弧，两弧交于点．则点即为所求．…………6分
画图正确．…………………………………………………………………9分
23．（本题9分）
解：连接AC、BD，AC与BD相交于点M，过点M作
ME⊥x轴于点E，过点C作CF⊥x轴于点F．
∵
∴AF=10，CF=4…………………………… …………………………2分
∵四边形为平行四边形．
∴EM=CM
∵ME⊥x轴，CF⊥x轴
∴∠MEA=∠CFA=90°
∴ME∥CF
∴ME∥CF，EM=CM
∴ME为△AFC的中位线．…………………………………………………4分
∴AE=AF=5, ME=CF=2
∴M（5，2）…………………………………………………………………6分
∵直线将平行四边形分成面积相等的两部分．
∴直线经过点M…………………………………………8分
将M（5，2）代入得：……………………………9分
24．（本题10分）
（1）5， 45， 35， 图略…………………………………………………5分
（2）150÷50%=300（人）……………………………………………6分
（3）C小区 ……………………………………………………………7分
可以从平均数或中位数等方面说明，说理合理就行。………………9分
宣传语通顺，有环保之意即可。……………………………………10分
A
B
M
北
东
C
S
W
1
2
25．（本题10分）
解：这艘船继续沿西南方向航行有触礁的危险．
理由如下：过点M作MC⊥AB于C．
由题意得：∠WAC=∠SAC=45°，∠SAM=75°
∴∠1=∠SAM-∠SAC=30°………………2分
设MC=x（海里），
在Rt△MAC中
AC=（海里）…………4分
∵灯塔M恰好在船的正西方向．
∴MB∥WA
∴∠2=∠WAC=45°
∴在Rt△MAC中 BC=MC=x（海里）…………………………5分
∵AB=40×=6（海里）
∵AC=AB+BC
∴…………………………………………………………7分
解得：……………………………………………………8分
∵MC=海里< 9海里．
∴有触礁的危险．……………………………………………………10分
26．（本题10分）
解：连续2次抛掷正方体骰子有36种情况，如下表，他们出现的可能性相同。………………………………………………………………………3分
二次函数化成顶点式：
∵、均为正整数
∴为奇数，可为1、3、5
当=1时，=4
当=3时，=6
当=5时，=4
∴满足条件的P点有3个即（1,4）、（3,6）、（5,4） ………………7分
∴点P（）在函数的图像上的概率是……………………………………………………………………10分
27．（本题12分）
解：（1）设1平方米荷花种植成本为x元，1平方米茉莉种植成本为y元．列方程组得：
………………………3分
解得: ………………………………………………………4分
∴
∴1平方米荷花种植成本为144元，
1平方米茉莉种植成本为72元．……………………………………5分
（2）设AE=AF=x米
则荷花的种植面积为：平方米．………………5分
∵点G、H、I分别是EF、CE、CF的中点．
∴HI、GH、GI均为△CEF的中位线
易证△GHI∽△CEF，且相似比为1：2
∴茉莉的种植面积为：平方米．……7分
可得方程：
×144+×72=7956……………………………………………………………………10分
整理得： 解得：（不合题意舍去）
∴AE的长度为2米．…………………………………………………12分
28．（本题14分）
解：（1）∵四边形ABCD是正方形 ∴AB=AD，∠BAF=∠DAO=90°
在△ABF和△ADO中 ∵∠ABF=∠ADO，AB=AD，∠BAF=∠DAO
∴△ABF≌△ADO ∴BF=DO…………………………………………4分
（2）∵A（）,B（）∴AO=m , BO=,AB=m
∵AE=DE
∴∠EBO=∠EBD
∵∠DAB=90°∴BD为直径∴∠BEO=∠BED=90°
又∵BE=BE∴△BEO≌△BED
∴BD=BO=
O
A
B
C
D
E
F
y
x
G
在Rt△BCD中BD=AB
∴=
∴m=
∵△ABF≌△ADO
∴AF=AO=m=
∴F点的坐标为……8分
∵抛物线l经过O，B（）
设l的解析式为
将F代入得：
∴抛物线l的解析式为…………………………………8分
（3）①如图，设直线BE与y轴相交于G，向上平移直线BE使平移后的直线经过原点O，由图像知，在平移前直线BE与新图像有1个公共点，平移到经过点O时与新图像有3个公共点.∴
设直线BE的解析式为，将B（），F代入易求出：…………………………………10分
当时， ∴
此时t的取值范围是：…………………………………11分
②如图，当直线BE向上平移至于抛物线相切后再向上平移时，直线BE与图象的交点又变为两个，设相切时直线BE的解析式为，则方程组有一个解，…………………………………12分
于是方程有两个相等的实数根，求出，
此时直线BE的解析式为，
直线BE与y轴的交点为（，）
∴此时t的取值范围是：…………………………………13分
综上所述：t的取值范围为：或………14分
2011年最新中考数学模拟试卷（60）
(考试时间：120分钟 总分：150 分)
注意事项：
1．本试卷共分两部分，第Ⅰ卷为选择题，第Ⅱ卷为非选择题．
2．所有试题的答案均填写在答题卡上，答案写在试卷上无效．
第Ⅰ卷 选择题（共24分）
一、选择题（下列各题所给答案中，只有一个答案是正确的，每小题3分，共24分）
1．的相反数是（ ▲ ）
A． B． C． D．
2．下列运算结果正确的是（ ▲ ）
A． B． C． D．
3．如图所示几何体的左视图是（ ▲ ）
4．将抛物线y=x2向左平移两个单位，再向上平移一个单位，可得到抛物线（ ▲ ）
A．y=(x－2) 2+1 B．y=(x－2) 2－1 C．y=(x+2) 2+1 D．y=(x+2) 2－1
5．如图，把一个矩形纸片ABCD沿EF折叠后，点D、C分别落在D′、C′的位置．若∠EFB，则∠AED′等于（ ▲ ）
A． B．
C． D．
6．给出下面四个命题：
(1) 全等三角形是相似三角形 (2) 所有的直角三角形都相似
(3) 所有的等边三角形都相似 (4) 顶角相等的两个等腰三角形相似
其中真命题的个数有（ ▲ ）
A．1个 B．2个 C．3个 D．4个
7．小丽家要买节能灯，于是到家电商场做调查，得到如下数据：
功率/W
正常寿命/h
单价/（元/只）
节能灯1
100
1000
1.5
节能灯2
30
1000
14
节能灯3
20
5000
25
第8题
这三种节能灯的照明效果相当．如果仅考虑费用（节能灯费用与耗电费用之和，用电度数=功率（W）×时间（h）÷1000，假设电费为0.60元/度）支出，小丽应选（ ▲ ）
A．节能灯3 B．节能灯2
C．节能灯1 D．任一种
8．如图，一个足够大的五边形，它的一个内角是120°，将120°角的顶点绕一个小正三角形的中心O旋转，则重叠部分的面积为正三角形面积的（ ▲ ）
A． B． C． D．不断变化
第Ⅱ卷 非选择题（共126分）
二、填空题（每题3分，共30分）
9．函数中，自变量x的取值范围是 ▲ ．
10．分解因式：9x2－4y2= ▲ ．
11．泰州长江大桥全长62余公里，核准总投资93.7亿元，建设工期为五年半．用科学记数法表示总投资为 ▲ 万元．[
12．若一组数据4，7，6，a，8的平均数为6，则这组数据的方差为 ▲ ．
13．若a＜b，则化简的结果为 ▲ ．
14．用半径为12cm，圆心角为的扇形做成一个圆锥模型的侧面，则此圆锥的高为 ▲
cm（结果保留根号）．
第15题
15．如图，AD和AC分别是⊙O的直径和弦，且∠CAD=30°，OB⊥AD交AC于点B，若OB=5，则BC等于 ▲ ．
16．某商店6月份的利润是2500元，要使8月份的利润达到3600元，则平均每月增长的百分率应该是 ▲ ．
17．按如图所示的程序计算，若开始输入的x值为6时，则第1次得到的输出结果为3，第2次得到的输出结果为8，……，于是第2010次输出的结果为 ▲ ．
18．如图，在由12个边长都为1且有一个锐角为60°的小菱形组成的网格中，点P是其中的一个格点，以点P为直角顶点作格点直角三角形（即顶点均在格点上的三角形），请写出所有可能的直角三角形斜边的长 ▲ ．
三、解答题
19．（本题满分8分）计算或解不等式组：
（1）计算 ；
（2）解不等式组
20．（本题满分8分）先化简，再求值：，其中．
21．（本题满分8分）对某校学生会倡导的“献爱心，送温暖”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据．下图是根据这组数据绘制的统计图，图中从左到右各矩形的高度之比为3：4：5：8：6，又知此次调查中捐款10元和30元的学生一共27人．
（1）这次抽样一共调查了多少学生？这组捐款数据的中位数是多少？
（2）若该校共有1560名学生，请估算全校学生共捐款多少元？
22．（本题满分8分）如图，F为正方形ABCD的对角线AC上一点，FE⊥AD于点E，M为CF的中点．
（1）求证：MB=MD；
（2）求证：ME=MB．
23．（本题满分10分）
有A、B两个口袋，A口袋中装有两个分别标有数字2，3的小球；B口袋中装有三个分别标有数字，4，的小球．小明先从A口袋中随机取出—个小球，用m表示所取球上的数字，再从B口袋中随机取出两个小球，用n表示所取球上的数字之和．
（1）用树状图法或列表法表示小明所取出的三个小球的所有可能结果
（2）求的值是整数的概率．
24．（本题满分10分）如图，AB是⊙O的直径，C是BA延长线上的一点，CD与⊙O相切于点D，连接OD，四边形PQRS是矩形，其中点P、Q在半径OA上，点R在半径OD上，点S在⊙O上．已知CD=4，CO=5，PQ=2RQ，
（1）求的值；
（2）求矩形PQRS的面积．
25．（本题满分10分）如图，泰州园博园中有一条人工河，河的两岸PQ、MN互相平行，河岸PQ上有一排间隔为50米的彩灯柱C、D、E、……，某人在河岸MN的A处测得∠DAN＝21º，然后沿河岸走了175米到达B处，测得∠CBN＝45º，求这条河的宽度．（参考数据：，）
26．（本题满分10分）如图，P1是反比例函数在第一象限图像上的一点，点A1 的坐标为(2，0)．
（1）当点P1的横坐标逐渐增大时，△P1O A1的面积将如何变化？
（2）若△P1O A1与△P2 A1 A2均为等边三角形，求此反比例函数的解析式及A2点的坐标．
27．(本题满分12分) 为了参观上海世博会，某公司安排甲、乙两车分别从相距300千米的上海、泰州两地同时出发相向而行，甲到泰州带客后立即返回，下图是它们离各自出发地的距离（千米）与行驶时间（小时）之间的函数图象．
（1）请直接写出甲离出发地的距离（千米）与行驶时间（小时）之间的函数关系式，并写出自变量的取值范围；
（2）当它们行驶4.5小时后离各自出发点的距离相等，求乙车离出发地的距离（千米）与行驶时间（小时）之间的函数关系式，并写出自变量的取值范围；
（3）在(2)的条件下，甲、乙两车从各自出发地驶出后经过多少时间相遇？
28．（本题满分12分）如图，抛物线的对称轴为直线x＝1，与x轴交于A、B两点，与y轴交于点C，其中A、C．
（1）求此抛物线的解析式；
（2）若此抛物线的顶点为P，将△BOC绕着它的顶点B顺时针在第一象限内旋转，旋转的角度为，旋转后的图形为△BO′C′．
①当O′C′ ∥CP时，求的大小；
②△BOC在第一象限内旋转的过程中，当旋转后的△BO′C′有一边与BP重合时，求△BO′C′不在BP上的顶点的坐标．
2011年最新中考数学模拟试卷（60）
一、选择题
1、A 2、D 3、B 4、C 5、D 6、C 7、A 8、C
二、填空题
9、 10、(3x+2y)(3x－2y) 11、9.37×105 12、2 13、1 14、 15、5
16、20% 17、6 18、2，4，，（答案不全扣2分，其余有正确答案一律得1分）
三、解答题
19、（1）原式= ················ （2分）
=1－1+2－4 ················ （3分）
=－2． ················ （4分）
（2）解第一个不等式得．············（1分 ）
解第二个不等式得．············（3分 ）
所以原不等式组的解集为．············（4分 ）
20、原式 ················（3分）
． ············（6分 ）
将代入计算，得原式．················（8分）
21、（1）由题意可设捐款10元、15元、20元、25元、30元的人数分别为3x、4x、5x、8x、6x．
则3x+6x=27，解得x=3． ············（2分）
所以捐款10元、15元、20元、25元、30元的人数分别为9、12、15、24、18．
所以一共抽查了9+12+15+24+18=78（人），············（4分）
这组捐款数据的中位数为25（元） ············（5分）
（2）全校学生共捐款约(9×10+12×15+15×20+24×25+18×30)÷78×1560=34200（元）············（8分）
22、（1）证明：因为四边形ABCD是正方形，
所以BC=DC，∠BCM =∠DCM．················ （1分）
又MC=MC，所以△BCM≌△DCM．
所以MB=MD． ················ （4分）
（2）证明：在直角梯形DEFC中，CD∥FE．
取DE的中点N，连接MN．
因为M为CF的中点，所以MN∥CD． ················ （6分）
又CD⊥DE，所以MN⊥DE．
所以MN是线段DE的垂直平分线．
所以MD=ME． ················ （7分）
由（1）知，MB=MD，所以ME=MB． ················ （8分）
（其它证法相应给分）
23、（1）用树状图表示取出的三个小球上的数字所有可能结果如下：（若学生将树状图列为6种等可能结果也正确）
··········（6分）
（列表法略）
（2）由树状图可知，所有可能的值分别为
，共有12种情况，且每种情况出现的可能性相同，其中的值是整数的情况有6种．所以的值是整数的概率P．················ （10分）
24、（1）因为CD与⊙O相切于点D，所以OD⊥CD．
在Rt△COD中，根据勾股定理，得
OD=．···············（2分）
在△ORQ和△OCD中，因为∠OQR=∠ODC=90°，∠ROQ=∠COD，
所以Rt△ORQ∽Rt△OCD，···············（4分）
所以，即，所以．···············（5分）（用三角函数解，相应给分）
（2）连接OS．设RQ=x，则PQ=2x． 由（1）知OQ=．
在Rt△OSP中，OP= PQ+OQ．···············（7分）
根据勾股定理，得，即，解得，···············（9分）
所以，即矩形PQRS的面积为．···············（10分）
25、作AS⊥PQ，CT⊥MN，垂足分别为S，T．
由题意知，四边形ATCS为矩形，
所以AS=CT，SC=AT．
设这条河的宽度为x米．
在Rt△ADS中，因为，
所以． ··················（3分）
在Rt△BCT中，因为，
所以． ··················（5分）
因为SD+DC =AB+BT，所以，··················（8分）
解得，即这条河的宽度为75米． ··················（10分）
（其它方法相应给分）
26、（1）△P1OA1的面积将逐渐减小．················（4分）
（2）作P1C⊥OA1，垂足为C，因为△P1O A1为等边三角形，
所以OC=1，P1C=，所以P1．··············（6分）
代入，得k=，所以反比例函数的解析式为．················（7分）
作P2D⊥A1 A2，垂足为D、设A1D=a，则OD=2+a，P2D=a，所以P2．····（8分）
代入，得，化简得，解得（取正值），
所以点A2的横坐标为．················（10分）
27．（1）甲离出发地的距离（千米）与行驶时间（小时）之间的函数关系式为
················ (4分)
（2）由题意知，图中AB与OC的交点P的橫坐标为4.5，
代入AB的解析式求得P点的纵坐标为80． ···················· (6分)
得OC解析式为y=40x，当y=300时，． ················ ( 7分)
即乙车离出发地的距离（千米）与行驶时间（小时）之间的函数关系式为． ················ ( 8分)
（3）由题意可知有两次相遇．①当时，，解得；
②当时，，解得．················ (11分)
综上所述，两车第一次相遇时间为出发后小时，第二次相遇时间为出发后6小时．················ (12分)
28、（1）由题意得，················（1分） 解得，
所以，此抛物线的解析式为．················（3分）
（2）①如图，顶点P为(1，4)， CP， BC，
BP，又因为
，所以∠PCB=90°．··········（5分）
又因为O′C′ ∥CP，所以O′C′⊥BC．所以点O′在BC上．所以=45°．··········（7分）
②如备用图1，当BC′与BP重合时，过点O′作O′D⊥OB于D．
因为∠PBC+∠CBO′=∠CBO′+∠ABO′=45°，所以∠ABO′=∠PBC．
则△DBO′∽△CBP，所以，所以，所以BD=3O′D．··········（9分）
设O′D= x，则BD=3x，根据勾股定理，得，解得，所以BD，所以点O′的坐标为(，)．··········（10分）
如备用图2，当BO′与BP重合时，过点B作x轴的垂线BE，过点C′作C′E⊥BE于E，因为∠PBE+∠EBC′=∠PBE+∠CBP=45°，所以∠EBC′=∠PBC．
所以△EBC′∽△CBP，所以，所以，所以BE=3C′E．
设C′E为y，则BE=3y，根据勾股定理，得，解得，所以BE，所以C′的坐标为(，)．··········（12分）
