中考数学冲击波考前纠错必备考点四三角形

中考数学冲击波考前纠错必备考点四三角形

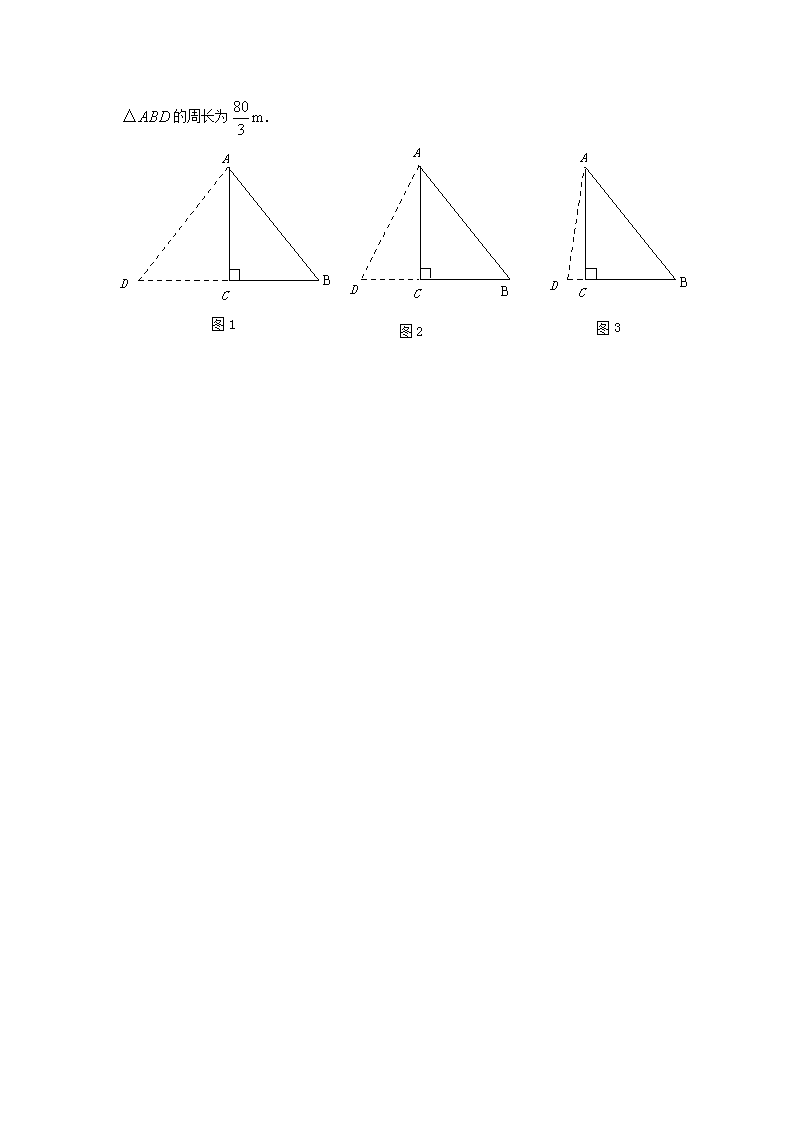
考点四 三角形 ‎【易错分析】‎ 易错点1：三角形的概念以及三角形的角平分线，中线，高线的特征与区别.‎ 易错点2：三角形三边之间的不等关系，注意其中的“任何两边”.‎ 易错点3：三角形的内角和，三角形的分类与三角形内外角性质，特别关注外角性质中的“不相邻”.‎ 易错点4：全等形，全等三角形及其性质，三角形全等判定.着重学会论证三角形全等，线段的倍分这些问题.‎ 易错点5：等腰（等边）三角形的定义以及等腰（等边）三角形的判定与性质，运用等腰（等边）三角形的判定与性质解决有关计算与证明问题，这里需注意分类讨论思想的渗入.‎ 易错点6：运用勾股定理及其逆定理计算线段的长，证明线段的数量关系，解决与面积有关的问题以及简单的实际问题.‎ 易错点7：将直角三角形，平面直角坐标系，函数，开放性问题，探索性问题结合在一起综合运用.‎ ‎【好题闯关】‎ 好题1.如图，△ABC中，∠A＝70°，∠B＝60°，点D在BC的延长线上，则∠ACD等于（ ）‎ A. 100° B. 120° C. 130° D. 150°‎ 解析：本题考查三角形外角的性质，三角形的一个外角等于和它不相邻的两个内角的和.学生易疏忽性质中的“不相邻”这三个字.‎ 答案：C 好题2.如图，为估计池塘岸边、两点的距离，小方在池塘的一侧选取一点，测得米，米，、间的距离不可能是（ ）‎ A．5米 B．10米 C． 15米 D．20米 解析：本例考查三角形三边之间的不等关系，三角形的任何两边之和大于第三边，任何两边之差小于第三边.学生易忽视概念里的“任何”两字.‎ 答案：A 好题3.已知等腰三角形的一个内角是30°，那么这个等腰三角形顶角的度数是（ ）‎ A.75° B. 120° C.30° D.30°或120°‎ 解析：等腰三角形的内角有顶角和底角之分，而已知一个内角是30°‎ ‎，并未说明是顶角还是底角，因此，本题很容易漏解.‎ 答案：D 好题4.如图，在△ABC和△ADE中，有以下四个论断：① AB＝AD，② AC＝AE，③ ∠C＝∠E，④ BC＝DE，请以其中三个论断为条件，余下一个论断为结论，写出一个真命题（用序号“JJJðJ”的形式写出）： ‎ 解析：本例是一个开放型问题，学生可以从①②③④中任选3个作为条件，而余下一个为结论，但构成的命题必须是真命题.所以，我们应根据三角形全等的判定方法去组合.这里，要注意“SSA”的错误做法.‎ 答案：①②④ð③，或 ②③④ð①‎ 好题5.已知的三边长分别为5，13，12，则的面积为（ ）‎ A．30 B．60 C．78 D．不能确定 解析：仔细观察三角形的三边就会发现：52+122=132，利用勾股定理的逆定理可以判断这个三角形是直角三角形，而且两直角边是5和12，根据面积公式即可得出结果.‎ 答案：A 好题6.有一块直角三角形的绿地，量得两直角边长分别为现在要将绿地扩充成等腰三角形，且扩充部分是以为直角边的直角三角形，求扩充后等腰三角形绿地的周长．‎ 解析：此例主要考点是直角三角形、勾股定理、等腰三角形，涉及到分类讨论的数学思想.思考分析时我们需注意两点：“等边对等角”适用的条件是在同一个三角形中，在不同三角形中不能用；等腰三角形“三线合一”指的是底边上的高、底边上的中线、顶角的平分线互相重合，对于腰上的高、腰上的中线，底角的平分线则不成立.‎ 答案：‎ 在中，，由勾股定理有：.‎ 扩充部分为扩充成等腰应分以下三种情况：‎ ‎①如图1，当时，可求，得的周长为32m．‎ ‎②如图2，当时，可求，由勾股定理得：，得的周长为 ‎③如图3，当为底时，设则由勾股定理得：，得 的周长为 A D C B A D B C A D B C 图1‎ 图2‎ 图3‎