- 2021-05-10 发布 |
- 37.5 KB |
- 12页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
本溪市2014年中考数学卷
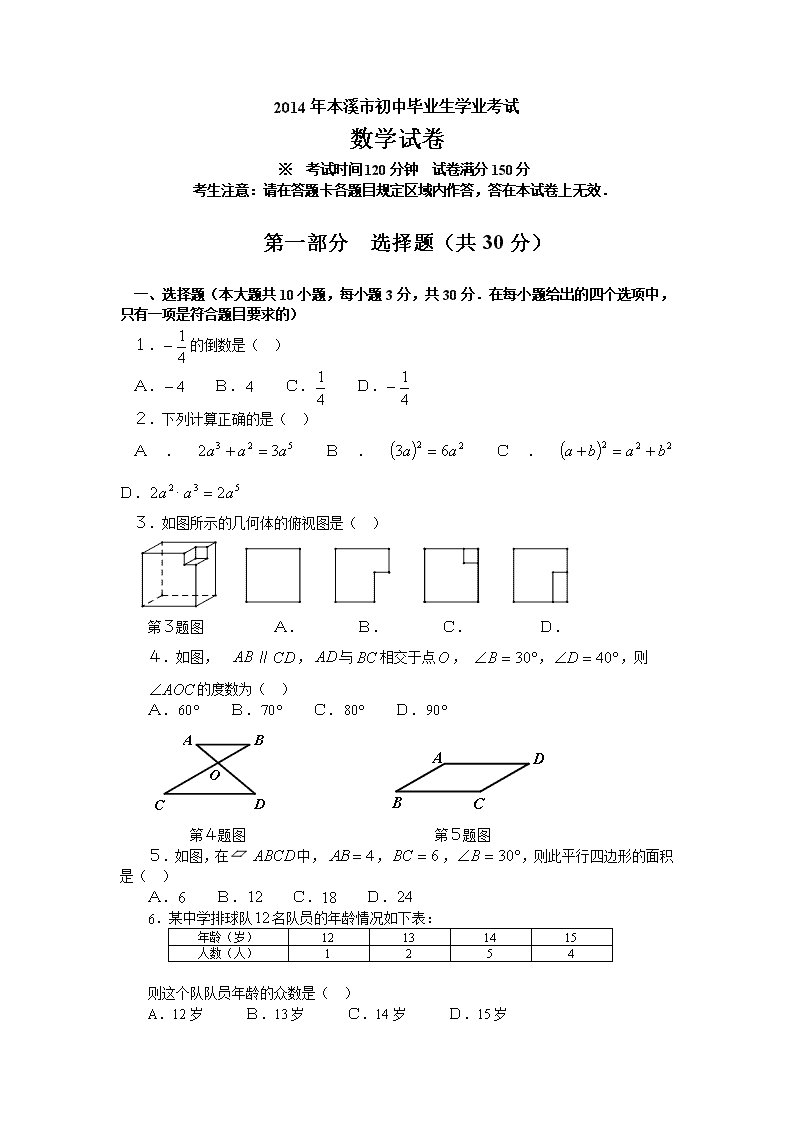
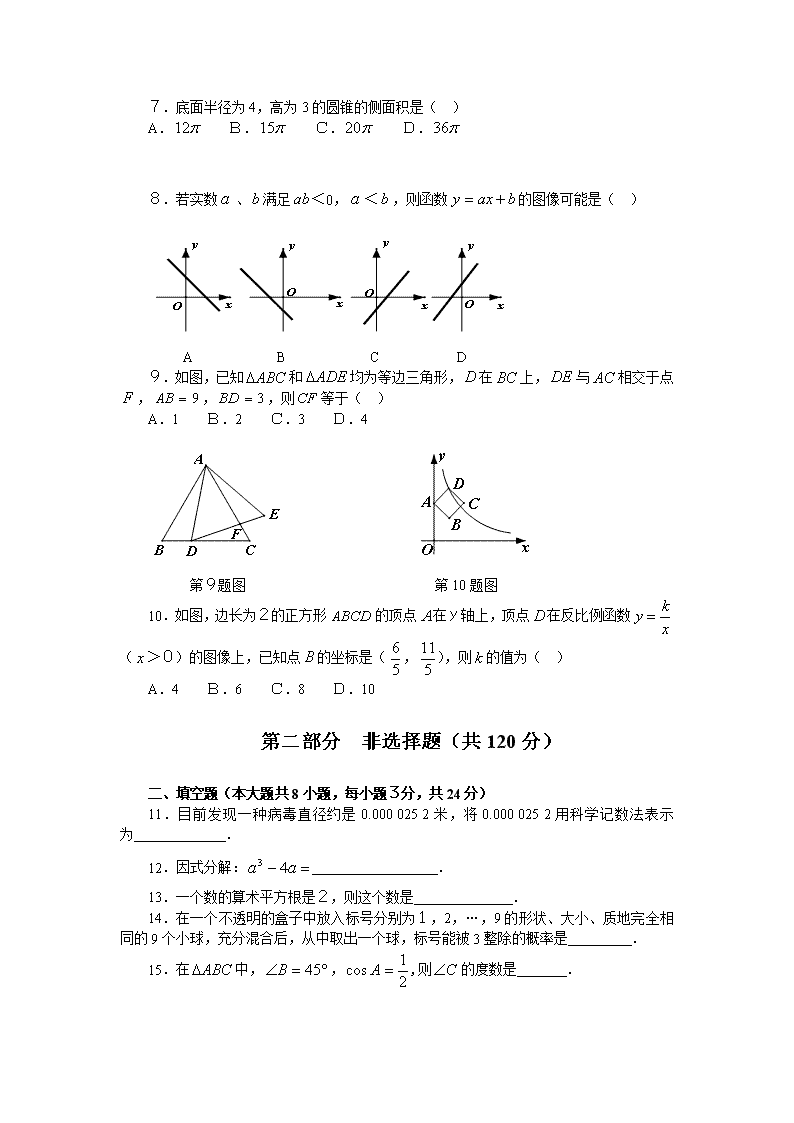
2014年本溪市初中毕业生学业考试 数学试卷 ※ 考试时间120分钟 试卷满分150分 考生注意:请在答题卡各题目规定区域内作答,答在本试卷上无效. 第一部分 选择题(共30分) 一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.的倒数是( ) A. B. C. D. 2.下列计算正确的是( ) A. B. C. D. 3.如图所示的几何体的俯视图是( ) 第3题图 A. B. C. D. 4.如图,∥,与相交于点, ,,则 的度数为( ) A. B. C. D. 第4题图 第5题图 5.如图,在中,,,,则此平行四边形的面积是( ) A. B. C. D. 6.某中学排球队名队员的年龄情况如下表: 年龄(岁) 12 13 14 15 人数(人) 1 2 5 4 则这个队队员年龄的众数是( ) A.12岁 B.13岁 C.14岁 D.15岁 7.底面半径为4,高为3的圆锥的侧面积是( ) A. B. C. D. 8.若实数、满足<0,<,则函数的图像可能是( ) A B C D 9.如图,已知和均为等边三角形,在上,与相交于点,,,则等于( ) A.1 B.2 C.3 D.4 第9题图 第10题图 10.如图,边长为2的正方形的顶点在y轴上,顶点在反比例函数(>0)的图像上,已知点的坐标是(,),则的值为( ) A.4 B.6 C.8 D.10 第二部分 非选择题(共120分) 二、填空题(本大题共8小题,每小题3分,共24分) 11.目前发现一种病毒直径约是0.000 025 2米,将0.000 025 2用科学记数法表示为 . 12.因式分解: . 13.一个数的算术平方根是2,则这个数是 . 14.在一个不透明的盒子中放入标号分别为1,2,…,9的形状、大小、质地完全相同的9个小球,充分混合后,从中取出一个球,标号能被3整除的概率是 . 15.在中,,,则的度数是 . 16.关于、的方程组的解是,则的值是 . 17.关于的一元二次方程,从,,三个数中任取一个数,作为方程中的值,再从剩下的两个数中任取一个数作为方程中的值,能使该一元二次方程有实数根的概率是 . 18.如图,已知,点绕点顺时针旋转后的对应点落在射线上,点绕点顺时针旋转后的对应点落在射线上,点绕点顺时针旋转后的对应点落在射线上,…,连接、、…,以此作法,则等于 度.(用含的代数式表示,为正整数) 第18题图 三、解答题(第19题10分,第20题12分,共22分) 19.先化简,再求值: ,其中 20.某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为,,,四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题: 图① 第20题图 图② (1)求本次被抽查的学生共有多少人? (2)将条形统计图和扇形统计图补充完整; (3)求扇形统计图中“”所在的扇形圆心角的度数; (4)估计全校“”等级的学生有多少人. 四、解答题(第21题12分,第22题12分,共24分) 21.晨光文具店用进货款1620元购进品牌的文具盒40个,品牌的文具盒60个.其中品牌文具盒的进货价比品牌文具盒的进货价多3元. (1)求、两种文具盒的进货单价; (2)已知品牌文具盒的售价为23元/个,若使这批文具盒全部售完后利润不低于500元,品牌文具盒的销售单价最少是多少?. 22.如图,已知在中,,,延长到,使,以为圆心,长为半径作⊙交延长线于点,连接. (1)求证:是⊙的切线; (2)若,求图中阴影部分的面积. 第22题图 五、解答题(满分12分) 23.某海域有、、三艘船正在捕鱼作业,船突然出现故障,向、两船发出紧急求救信号,此时船位于船的北偏西72°方向,距船24海里的海域. 船位于船的北偏东33°方向,同时又位于船的北偏东78°方向. (1)求的度数; (2)船以每小时30海里的速度前去救援, 问多长时间能到出事地点.(结果精确到0.01小时) (参考数据:,) 第23题图 六、解答题(满分12分) 24.国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进、两种型号的低排量汽车,其中型汽车的进货单价比型汽车的进货单价多2万元;花50万元购进型汽车的数量与花40万元购进型汽车的数量相同.销售中发现型汽车的每周销量 (台)与售价(万元/台)满足函数关系,型汽车的每周销量 (台)与售价(万元/台)满足函数关系 (1)求、两种型号的汽车的进货单价; (2)已知型汽车的售价比型汽车的售价高2万元/台.设型汽车售价为万元/台,每周销售这两种车的总利润为万元,求与的函数关系式, 、两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元? 七、解答题(满分12分) 25.如图,在和中,,, ,不动,绕点旋转,连接、,为的中点,连接. (1)如图①,当时,求证:; (2)当时,(1)的结论是否成立?请结合图②说明理由. 图① 第25题图 图② 八、解答题(满分14分) 26.如图,直线与轴、轴分别交于、两点,抛物线经过、两点,与轴的另一个交点为,连接. (1)求抛物线的解析式及点的坐标; (2)点在抛物线上,连接,当时,求点的坐标; (3)点从点出发,沿线段由向运动,同时点从点出发,沿线段由向运动,、的运动速度都是每秒1个单位长度,当点到达点时,、同时停止运动.试问在坐标平面内是否存在点,使、运动过程中的某一时刻,以、、、为顶点的四边形为菱形?若存在,直接写出点的坐标;若不存在,说明理由. 第26题图 备用图 备用图 [来源:学科网ZXXK]查看更多