中考数学试题及答案分类汇编图形的变换

中考数学试题及答案分类汇编图形的变换

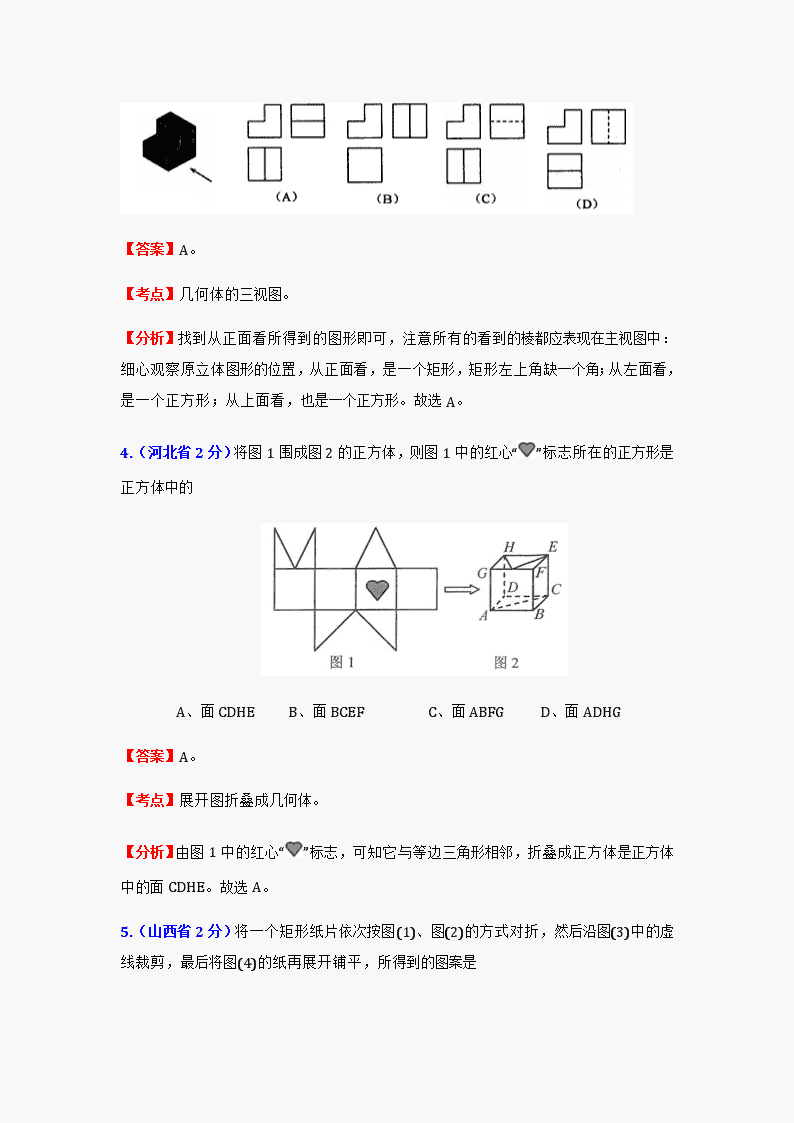
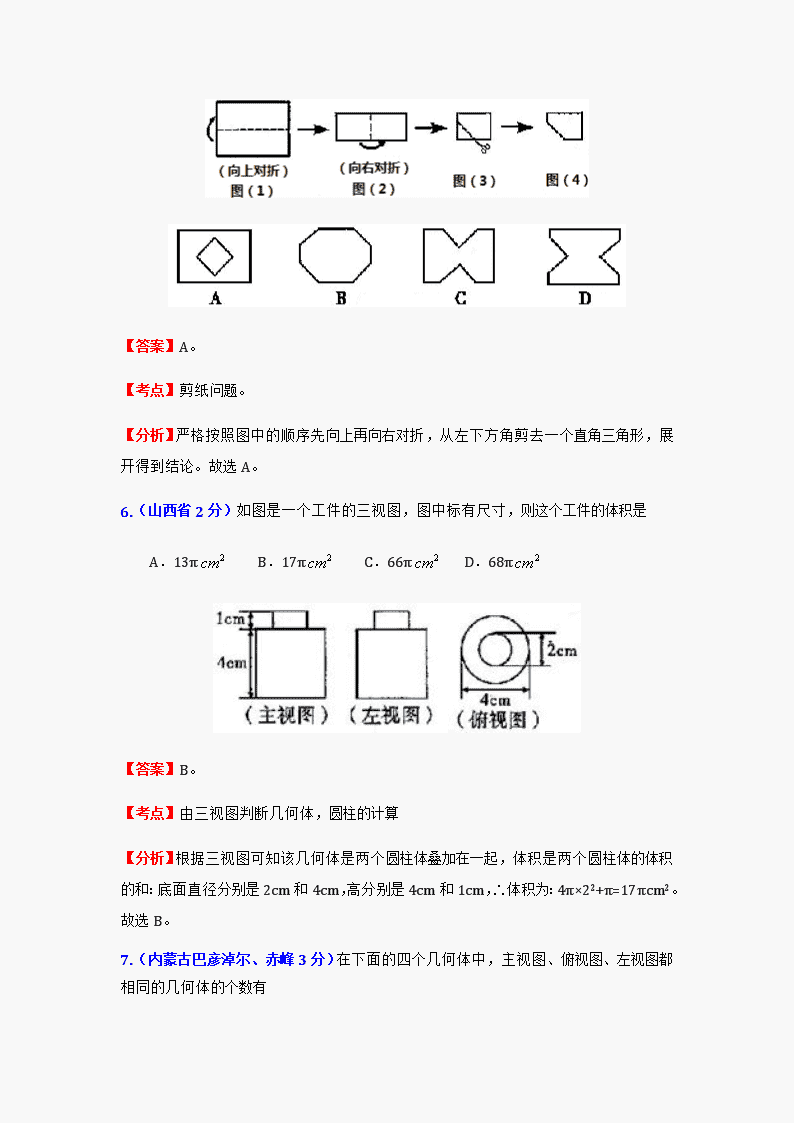
‎2012中考数学试题及答案分类汇编：图形的变换 一、 选择题 ‎1. （北京4分）下列图形中，即是中心对称又是轴对称图形的是 ‎ A、等边三角形 B、平行四边形 C、梯形 D、矩形 ‎【答案】D。‎ ‎【考点】中心对称和轴对称图形。‎ ‎【分析】根据轴对称图形与中心对称图形的概念，轴对称图形两部分沿对称轴折叠后可重合；中心对称图形是图形沿对称中心旋转180度后与原图重合。从而有A、是轴对称图形，不是中心对称图形．故本选项错误；B、是不是轴对称图形，是中心对称图形．故本选项错误；C、是轴对称图形，不是中心对称图形．故本选项错误；D、既是轴对称图形，又是中心对称图形．故本选项正确。故选D。‎ ‎2.（天津3分）下列汽车标志中，可以看作是中心对称图形的是 ‎【答案】A。‎ ‎【考点】中心对称图形。‎ ‎【分析】根据在平面内，一个图形绕某个点旋转180°，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形的定义，直接得出结果。‎ ‎3.（天津3分）下图是一支架(一种小零件)，支架的两个台阶的高度和宽度都是同一长度．则它的三视图是 ‎【答案】A。‎ ‎【考点】几何体的三视图。‎ ‎【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中：细心观察原立体图形的位置，从正面看，是一个矩形，矩形左上角缺一个角；从左面看，是一个正方形；从上面看，也是一个正方形。故选A。‎ ‎4.（河北省2分）将图1围成图2的正方体，则图1中的红心“”标志所在的正方形是正方体中的 ‎ ‎ A、面CDHE B、面BCEF C、面ABFG D、面ADHG ‎【答案】A。‎ ‎【考点】展开图折叠成几何体。‎ ‎【分析】由图1中的红心“”标志，可知它与等边三角形相邻，折叠成正方体是正方体中的面CDHE。故选A。‎ ‎5.（山西省2分）将一个矩形纸片依次按图(1)、图(2)的方式对折，然后沿图(3)中的虚线裁剪，最后将图(4)的纸再展开铺平，所得到的图案是 ‎ ‎【答案】A。‎ ‎【考点】剪纸问题。‎ ‎【分析】严格按照图中的顺序先向上再向右对折，从左下方角剪去一个直角三角形，展开得到结论。故选A。‎ ‎6.（山西省2分）如图是一个工件的三视图，图中标有尺寸，则这个工件的体积是 ‎ A．13π B．17π C．66π D．68π ‎【答案】B。‎ ‎【考点】由三视图判断几何体，圆柱的计算 ‎【分析】根据三视图可知该几何体是两个圆柱体叠加在一起，体积是两个圆柱体的体积的和：底面直径分别是2cm和4cm，高分别是4cm和1cm，∴体积为：4π×22+π=17πcm2。故选B。‎ ‎7.（内蒙古巴彦淖尔、赤峰3分）在下面的四个几何体中，主视图、俯视图、左视图都相同的几何体的个数有 ‎ ‎ A、1个 B、2个 C、3个 D、4个 ‎【答案】A。‎ ‎【考点】简单几何体的三视图。‎ ‎【分析】主视图、俯视图、左视图是分别从物体正面、上面和左面看，所得到的图形，‎ 圆柱主视图、俯视图、左视图分别是长方形、圆、长方形，主视图、左视图与俯视图不相同；‎ 圆锥主视图、俯视图、左视图分别是三角形、有圆心的圆、三角形，主视图、左视图与俯视图不相同；‎ 球主视图、俯视图、左视图都是圆，主视图、俯视图、左视图都相同；‎ 长方体主视图、俯视图、左视图是大小不同的矩形，三视图不相同。‎ 共1个同一个几何体的主视图与俯视图、左视图相同。故选A。‎ ‎8.（内蒙古包头3分）下列几何体各自的三视图中，只有两个视图相同的是 ‎ ‎①正方体 ‎②圆锥体 ‎③球体 ‎④圆柱体 A．①③ B．②③ C．③④ D．②④‎ ‎【答案】D。‎ ‎【考点】简单几何体的三视图。‎ ‎【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，分别分析四个几何体的三视图，从中找出只有两个视图相同的几何体，可得出结论：①正方形的主、左和俯视图都是正方形；②圆锥的主、左视图是三角形，俯视图是圆；③球体的主、左和俯视图都是圆形；④圆柱的主、左视图是长方形，俯视图是圆。只有两个视图相同的几何体是圆锥和圆柱。故选D。‎ ‎9.（内蒙古呼和浩特3分）已知圆柱的底面半径为1，母线长为2，则圆柱的侧面积为 ‎ A、2 B、4 C、2π D、4π ‎【答案】D。‎ ‎【考点】圆柱的展开。‎ ‎【分析】圆柱沿一条母线剪开，所得到的侧面展开图是一个矩形，它的长是底面圆的周长，即2π，宽为母线长为‎2cm，所以它的面积为4πcm2。故选D。‎ ‎10.（内蒙古呼和浩特3分）将如图所示表面带有图案的正方体沿某些棱展开后，得到的图形是 ‎ A、 B、C、 D、‎ ‎【答案】C。‎ ‎【考点】几何体的展开图。‎ ‎【分析】由原正方体知，带图案的三个面相交于一点，而通过折叠后A、B都不符合，且D折叠后图案的位置正好相反，所以能得到的图形是C。故选C。‎ ‎11.（内蒙古呼伦贝尔3分）如图，几何体的俯视图是 ‎ ‎【答案】C。‎ ‎【考点】简单组合体的三视图。‎ ‎【分析】找到从上面看所得到的图形即可：从上面看易得里层有4个正方形，外层左边有1个正方形。故选C。‎ ‎12.（内蒙古乌兰察布3分）如图是由五个相同的小正方体搭成的几何体，它的主视图是 ‎【答案】B。‎ ‎【考点】简单组合体的三视图。‎ ‎【分析】找到从正面看所得到的图形即可：从正面看易得第一层左边有1个正方形，第二层有3个正方形。故选B。‎ ‎13.（内蒙古乌兰察布3分）己知O为圆锥的顶点，M 为圆锥底面上一点，点 P 在 OM上．一只锅牛从P点出发，绕圆锥侧面爬行，回到P点时所爬过的最短路线的痕迹如图所示,若沿OM将圆锥侧面剪开并展开，所得侧面展开图是 ‎【答案】D。‎ ‎【考点】圆锥的展开，扇形的轴对称性，线段的性质。‎ ‎【分析】根据两点之间比下有余最短的性质，锅牛爬过的最短路线应是一条线段：根据扇形的轴对称性，选择D正确。故选D。‎ ‎14.（内蒙古乌兰察布3分）将正方体骰子（相对面上的点数分别为 1 和 6 、 2 和 5 、 3 和 4 ）放置于水平桌面上 ，如图 ① ．在图 ② 中，将骰子向右翻滚 90 ，然后在桌面上按逆时针方向旋转 90， 则完成一次变换．若骰子的初始位置为图①所示的状态，那么按上述规则连续完成10次变换后，骰子朝上一面的点数是 A . 6 B . 5 C . 3 D . 2 ‎ ‎【答案】B。‎ ‎【考点】分类归纳（图形变化类）。‎ ‎【分析】寻找规律：‎ ‎ 可知，按上述规则连续完成3次变换后，骰子回到初始位置，因此连续完成10次变换后，骰子与完成1次变换的状态相同。故选B。‎ 一、 填空题 ‎1.（北京4分）若下图是某几何体的表面展开图，则这个几何体是　 ▲ 　．‎ ‎【答案】圆柱。‎ ‎【考点】平面图形的折叠和立体图形的表面展开。‎ ‎【分析】由平面图形的折叠及立体图形的表面展开图的特点知道，一个长方形和两个圆折叠后，能围成的几何体是圆柱。‎ ‎2.（河北省3分）如图1，两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向右平移到△A’B’D’的位置，得到图2，则阴影部分的周长为 ▲ ．‎ ‎【答案】2。‎ ‎【考点】平移的性质，等边三角形的判定和性质。‎ ‎【分析】如图，∵两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向右平移到△A’B’D’的位置，‎ ‎∴A′M=A′N=MN，MO=DM=DO，OD′=D′E=OE，EG=EC=GC，B′G=RG=RB′，‎ ‎∴OM+MN+NR+GR+EG+OE=A′D′+CD=1+1=2。‎ ‎3.（河北省3分）如图，给正五边形的顶点依次编号为1，2，3，4，5．若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”．‎ 如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”．‎ 若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号是 ▲ ．‎ ‎【答案】3。‎ ‎【考点】分类归纳（图形的变化类）。‎ ‎【分析】根据“移位”的特点，寻找规律，得出结论：‎ ‎∵小宇在编号为2的顶点上时，那么他应走2个边长，即从2→3→4为第1次“移位”，这时他到达编号为4的顶点；然后从4→5→1→2→3为第2次“移位”， 然后从3→4→5→1为第3次“移位”； 然后从1→2为第4次“移位”。‎ ‎∴2→3→4→5→1→2四次移位为一个循环返回顶点2。‎ ‎∴第10次“移位”后，他所处顶点的编号与第2次“移位”的编号3相同，即他所处顶点的编号是3。‎ ‎4.（山西省3分）如图是用相同长度的小棒摆戍的一组有规律的图案，图案(1)需要4根小棒，图案(2)需要10根小棒……，按此规律摆下去，第个图案需要小棒 ▲ 根(用含有的代数式 表示)。‎ ‎【答案】6n－2。‎ ‎【考点】分类归纳（图形的变化类）。‎ ‎【分析】找出规律：如图可知，后一幅图总是比前一幅图多两个菱形，即多6根小棒，‎ 图案（1）需要小棒：6×1－2=4（根）；图案（2）需要小棒：6×2－2=10（根）；‎ 图案（3）需要小棒：6×3－2=16（根）；图案（4）需要小棒：6×4－2=22（根）；‎ 则第n个图案需要小棒：6n－2根。‎ ‎5.（山西省3分）如图，△ABC是等腰直角三角形，∠ACB=90°，AB=AC，把△ABC绕点A按顺时针方向旋转45°后得到△AB’C’，若AB=2，则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 ▲ (结果保留π)。‎ ‎【答案】。‎ ‎【考点】旋转的性质，等腰三角形的性质，勾股定理，扇形和三角形面积。‎ ‎【分析】根据题意，阴影部分的面积为（S扇形ABB′－S△ABC）＋（S△AB′C′－S扇形ACC′）‎ ‎ 由勾股定理，得AC=。由等腰三角形的性质，得两扇形的圆心角为450。‎ ‎ ∴阴影部分的面积为 a a b b 图1‎ 图2‎ ‎6.（内蒙古包头3分）如图，边长为a的正方形中有一个边长为b的小正方形，若将图1的阴影部分拼成一个长方形，如图2，比较图1和图2的阴影部分的面积，你能得到的公式是　 ▲ 　．‎ ‎【答案】a2﹣b2=（a+b）（a﹣b）。‎ ‎【考点】平方差公式的几何意义。‎ ‎【分析】根据题意分别求得图1与图2中阴影部分的面积，由两图形阴影面积相等，即可求得答案：‎ 图1中阴影部分的面积为：a2﹣b2；图2中阴影部分的面积为：（a+b）（a﹣b）。‎ ‎∵两图形阴影面积相等，∴可以得到的结论是：a2﹣b2=（a+b）（a﹣b）。‎ ‎7.（内蒙古包头3分）如图，把矩形纸片OABC放入平面直角坐标系中，使OA，OC分别落在x轴、y轴上，连接AC，将矩形纸片OABC沿AC折叠，使点B落在点D的位置，若B（1，2），则点D的横坐标是　 ▲ 　．‎ ‎【答案】－。‎ ‎【考点】翻折变换（折叠问题），矩形的性质，平行的判定和性质，折叠对称的性质，相似三角形的判定和性质，坐标与图形性质。‎ ‎【分析】过点D作DF⊥OA于F，‎ ‎∵四边形OABC是矩形，∴OC∥AB。∴∠ECA=∠CAB。‎ 根据折叠对称的性质得：∠CAB=∠CAD，∠CDA=∠B=90°，‎ ‎∴∠ECA=∠EAC，∴EC=EA。‎ ‎∵B（1，2），∴AD=AB=2。‎ 设OE=x，则AE=EC=OC－OE=2－x，‎ 在Rt△AOE中，AE2=OE2＋OA2，即（2－x）2=x2＋1，‎ 解得：x=。∴OE=，AE=，‎ ‎∵DF⊥OA，OE⊥OA，∴OE∥DF，∴△AOE∽△AFD。‎ ‎∴。∴AF=。‎ ‎∴OF=AF－OA=。∴点D的横坐标为：－。‎ ‎8.（内蒙古呼伦贝尔3分）用火柴棒按下列方式搭图形，按照这种方式搭下去，搭第n个图形需 ▲ ‎ ‎ 根火柴棒。‎ ‎【答案】6＋6n。‎ ‎【考点】分类归纳（图形变化类）。‎ ‎【分析】找出规律：观察可知，后一个图形比前一个图形多6根火柴棒 。第二个图形需12＋6（2－1）根火柴棒，第三个图形需12＋6（3－1）根火柴棒，······因此第n个图形需12＋6（n－1）＝6＋6n根火柴棒。‎ ‎9.（内蒙古乌兰察布4分）将一些半径相同的小圆按如图所示的规律摆放，请仔细观察，第 n 个图形 有 ▲ 个小圆 · （用含 n 的代数式表示）‎ 第1个图形 第 2 个图形 第3个图形 第 4 个图形 ‎【答案】。‎ ‎【考点】分类归纳（图形变化类）。‎ ‎【分析】寻找规律：第1个图形中间有2＝1×2个小圆，第2个图形中间有6＝2×3个小圆，第3个图形中间有12＝3×4个小圆，第4个图形中间有20＝4×5个小圆，······第n个图形中间有n（n＋1）个小圆。共有4＋n（n＋1）＝个小圆。‎ 一、 解答题 ‎1.（河北省8分）如图，在6×8网格图中，每个小正方形边长均为1，点0和△ABC的顶点均为小正方形的顶点．‎ ‎（1）以O为位似中心，在网络图中作△A′B′C′，使△AA′B′C′和△ABC位似，且位似比为 1：2；‎ ‎（2）连接（1）中的AA′，求四边形AA′C′C的周长．（结果保留根号）‎ ‎【答案】解：（1）如图所示：‎ ‎（2）在Rt△OA′C′中，OA′=OC′=2，‎ 根据勾股定理，得A′C′=2。‎ 同理可得AC=4。‎ 又AA′=CC′=2．‎ ‎∴四边形AA′C′C的周长=4＋6。‎ ‎【考点】作图（位似变换），勾股定理。‎ ‎【分析】（1）根据位似比是1：2，画出以O为位似中心的△A′B′C′。‎ ‎（2）根据勾股定理求出AC，A′C′的长，由于AA′，CC′的长易得，相加即可求得四边形AA′C′C的周长。‎ ‎2.（内蒙古包头10分）在Rt△ABC中，AB=BC=5，∠B=90°，将一块等腰直角三角板的直角顶点放在斜边AC的中点O处，将三角板绕点O旋转，三角板的两直角边分别交AB，BC或其延长线于E，F两点，如图（1）与（2）是旋转三角板所得图形的两种情况．‎ ‎（1）三角板绕点O旋转，△OFC是否能成为等腰直角三角形？若能，指出所有情况（即给出△OFC是等腰直角三角形时BF的长），若不能，请说明理由；‎ ‎（2）三角板绕点O旋转，线段OE和OF之间有什么数量关系？用图（1）或（2）加以证明；‎ ‎（3）若将三角板的直角顶点放在斜边上的点P处（如图（3）），当AP：AC=1：4时，PE和PF有怎样的数量关系？证明你发现的结论．‎ ‎【答案】解：（1）△OFC能成为等腰直角三角形。‎ ‎①当F为BC的中点时，∵O点为AC的中点，∴OF∥AB。∴CF=OF=。‎ ‎∵AB=BC=5，∴BF=。‎ ‎②当B与F重合时，∵OF=OC=，∴BF=0。‎ ‎（2）OE=OF。以图（1）证明如下：‎ 如图，连接OB，‎ ‎∵由（1）的结论可知，BO=OC=，‎ ‎∵∠EOB=900－∠BOF =∠FOC，∠EBO=450=∠C，‎ ‎∴△OEB≌△OFC（ASA）。∴OE=OF。‎ ‎（3）PE：PF=1：4。证明如下：‎ 如图，过点P作PM⊥AB，PN⊥BC，‎ ‎∵∠EPM+∠EPN=∠EPN+∠FPN=90°，‎ ‎∴∠EPM=∠FPN。‎ ‎∵∠FMP=∠FNP=90°，∴△PNF∽△PME。‎ ‎∴PM：PN=PE：PF。‎ ‎∵△APM和△PNC为等腰三角形，∴△APM∽△PNC，‎ ‎∴PM：PN=AP：PC。‎ ‎∵PA：AC=1：4，∴PE：PF=1：4。‎ ‎【考点】等腰直角三角形的判定和性质，三角形中位线的性质，旋转的性质，全等三角形的判定和性质，相似三角形的判定和性质。‎ ‎【分析】（1）由题意可知，①当F为BC的中点时，由AB=BC=5，可以推出CF和OF的长度，即可推出BF的长度，②当B与F重合时，根据直角三角形的相关性质，即可推出OF的长度，即可推出BF的长度。‎ ‎（2）连接OB，由已知条件推出△OEB≌△OFC，即可推出OE=OF。‎ ‎（3）过点P作PM⊥AB，PN⊥BC，结合图形推出△PNF∽△PME，△APM∽△PNC，继而推出PM：PN=PE：PF，PM：PN=AP：PC，根据已知条件即可推出PA：AC=PE：PF=1：4。‎