- 2021-05-10 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
反比例函数与几何图形中考填空题第16题
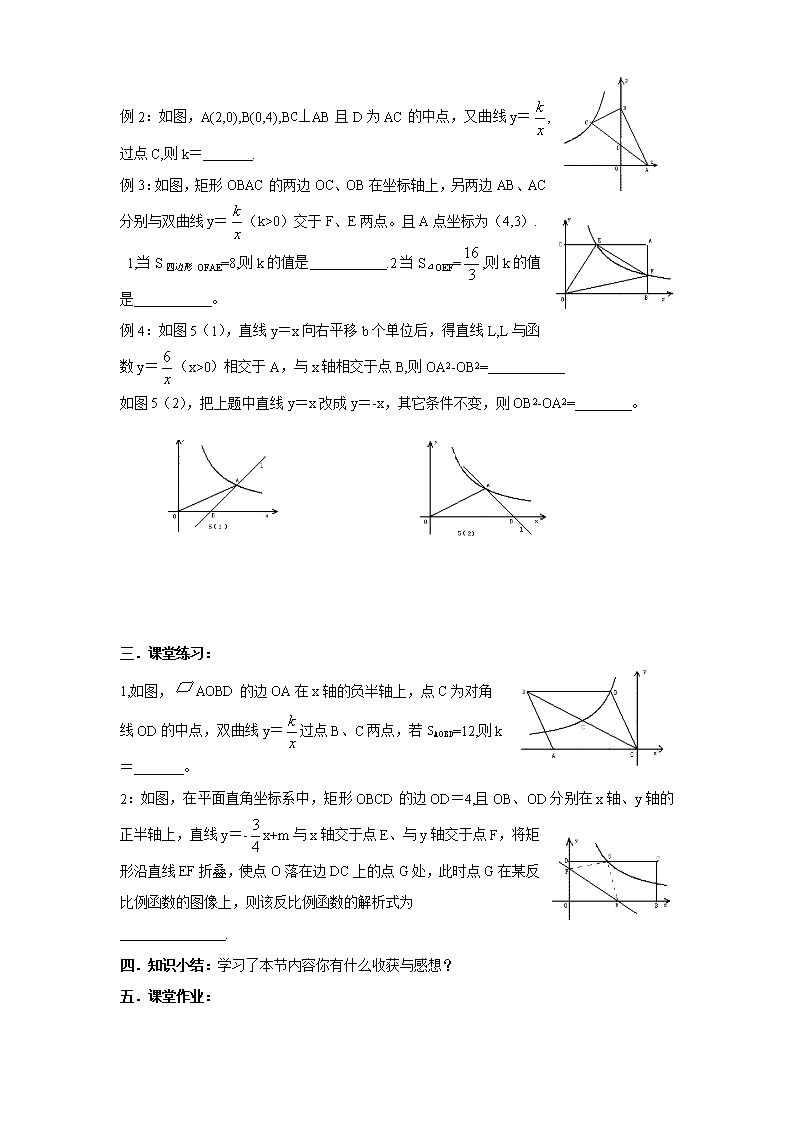
反比例函数与几何图形(中考填空题第16题) 横店中学 张元生 教学目标: 知识与技能 1、 掌握反比例函数的性质,能根据条件确定反比例函数的表达式。 2.能利用反比例函数的性质探索、解决有关的几何问题。 思想与方法 以反比例函数为载体,结合几何图形灵活运用数形结合法、整体代入法等思想方法,通过三角形面积与全等、相似、平移、轴对称、中心对称等变换形式综合解决问题。 情感与态度 1. 培养学生积极参与数学学习活动的兴趣,增强数学学习的好奇心和求知欲, 2. 使学生感受在数学学习活动中获得成功的体验,锻炼学生克服困难的意志,建立自信心。 3. 培养学生科学探索的精神。 重点 反比例函数的性质,结合几何图形利用反比例函数的性质解决问题。 难点 抓住图形特征,采取正确的思维途径解决问题。 过程 一.预备知识: 二.例题讲解: 例1:如图正方形ABCD的边BC在x轴的负半轴上,E(-,n)是对角线AC的中点,函数y=(x <0)的图像过D、E两点,则k= 。 例2:如图,A(2,0),B(0,4),BC⊥AB且D为AC的中点,又曲线y=,过点C,则k= . 例3:如图,矩形OBAC的两边OC、OB在坐标轴上,另两边AB、AC分别与双曲线y=(k>0)交于F、E两点。且A点坐标为(4,3). 1,当S四边形OFAE=8,则k的值是 .2当S⊿OEF=,则k的值是 。 例4:如图5(1),直线y=x向右平移b个单位后,得直线L,L与函数y=(x>0)相交于A,与x轴相交于点B,则OA2-OB2= 如图5(2),把上题中直线y=x改成y=-x,其它条件不变,则OB2-OA2= 。 三.课堂练习: 1,如图,AOBD的边OA在x轴的负半轴上,点C为对角线OD的中点,双曲线y=过点B、C两点,若SAOBD=12,则k= 。 2:如图,在平面直角坐标系中,矩形OBCD的边OD=4,且OB、OD分别在x轴、y轴的正半轴上,直线y=-x+m与x轴交于点E、与y轴交于点F,将矩形沿直线EF折叠,使点O落在边DC上的点G处,此时点G在某反比例函数的图像上,则该反比例函数的解析式为 . 四.知识小结:学习了本节内容你有什么收获与感想? 五.课堂作业: 1,如图,点E、F在双曲线y=上,直线FE交y轴与A点,AE=EF,FM⊥x轴于点M,则S⊿AME= . 2,如图,直线y=x+1与坐标轴分别交于A、B两点为,与双曲线y=(x>0)交于点C,过C作AC的垂线交x轴于点D(2,0),则k的值是 。 3,如图,直线y=kx(k>0)与双曲线y=交于A、B两点,若A、B两点的坐标分别为A(x1,y1)、B(x2,y2),则x1y2+x2y1的值为 。查看更多