江苏省镇江市2008年初中毕业升学考试数学试卷

江苏省镇江市2008年初中毕业升学考试数学试卷

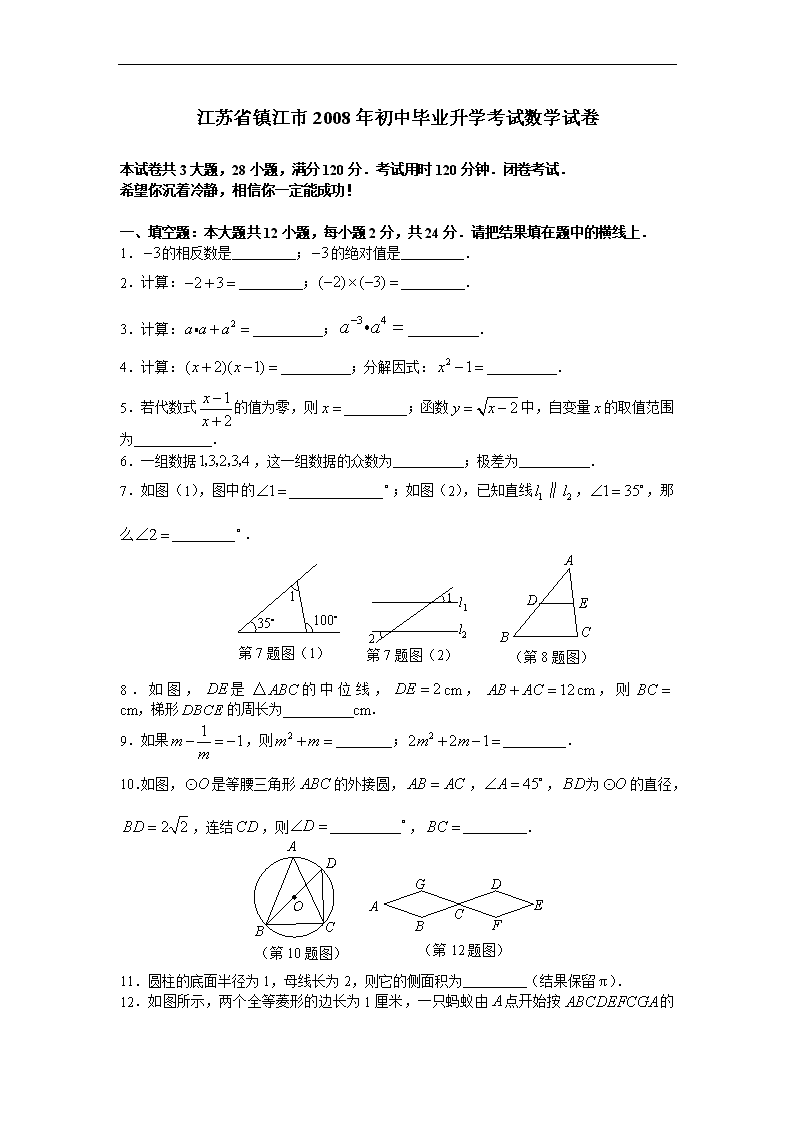
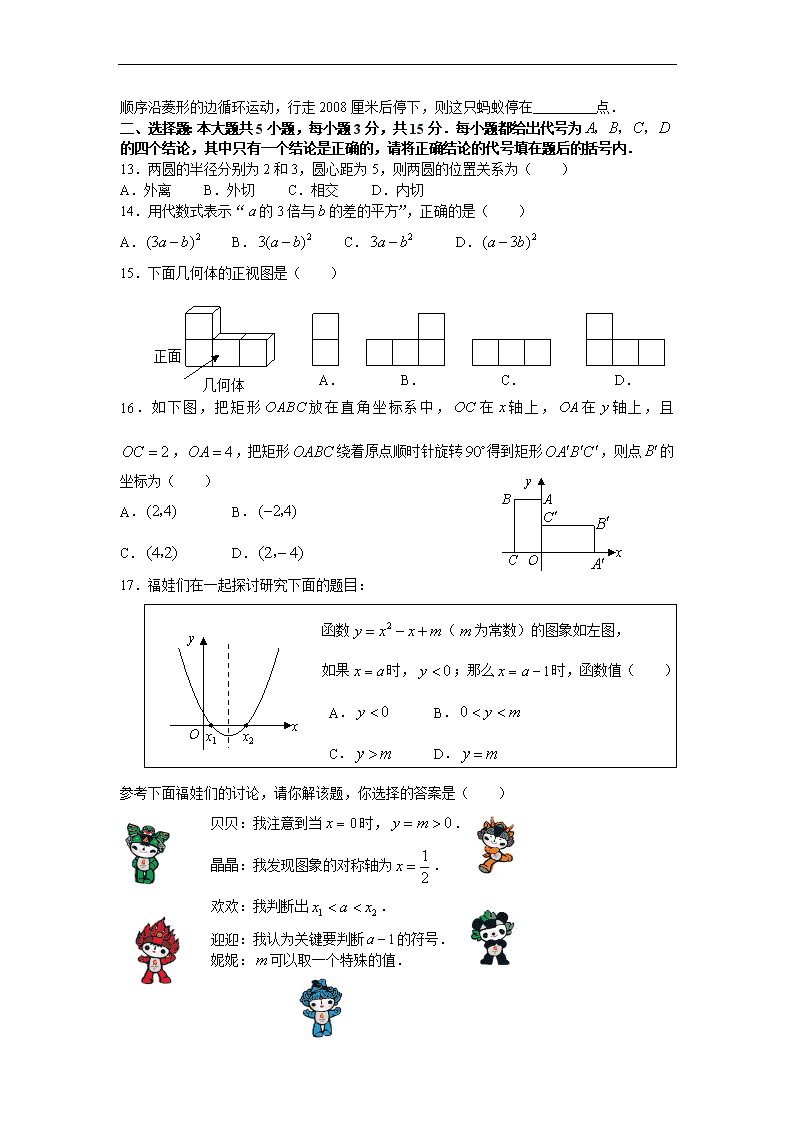
江苏省镇江市2008年初中毕业升学考试数学试卷 本试卷共3大题，28小题，满分120分．考试用时120分钟．闭卷考试．‎ 希望你沉着冷静，相信你一定能成功！‎ 一、填空题：本大题共12小题，每小题2分，共24分．请把结果填在题中的横线上．‎ ‎1．的相反数是 ；的绝对值是 ．‎ ‎2．计算： ； ．‎ ‎3．计算： ； ．‎ ‎4．计算： ；分解因式： ．‎ ‎5．若代数式的值为零，则 ；函数中，自变量的取值范围为 ．‎ ‎6．一组数据，这一组数据的众数为 ；极差为 ．‎ 第7题图（1）‎ ‎1‎ 第7题图（2）‎ ‎1‎ ‎2‎ l1‎ l2‎ A E C B D ‎（第8题图）‎ ‎7．如图（1），图中的 ；如图（2），已知直线，，那么 ．‎ ‎8．如图，是的中位线，cm，cm，则 cm，梯形的周长为 cm．‎ ‎9．如果，则 ； ．‎ A D C B O ‎（第10题图）‎ ‎10．如图，是等腰三角形的外接圆，，，为的直径，，连结，则 ， ．‎ C A F D E B G ‎（第12题图）‎ ‎11．圆柱的底面半径为1，母线长为2，则它的侧面积为 （结果保留）．‎ ‎12．如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由点开始按 的顺序沿菱形的边循环运动，行走2008厘米后停下，则这只蚂蚁停在 点．‎ 二、选择题：本大题共5小题，每小题3分，共15分．每小题都给出代号为的四个结论，其中只有一个结论是正确的，请将正确结论的代号填在题后的括号内．‎ ‎13．两圆的半径分别为2和3，圆心距为5，则两圆的位置关系为（ ）‎ A．外离 B．外切 C．相交 D．内切 ‎14．用代数式表示“的3倍与的差的平方”，正确的是（ ）‎ A． B． C． D．‎ ‎15．下面几何体的正视图是（ ）‎ 几何体 正面 A．‎ B．‎ C．‎ D．‎ x A O C B y ‎16．如下图，把矩形放在直角坐标系中，在轴上，在轴上，且，，把矩形绕着原点顺时针旋转得到矩形，则点的坐标为（ ）‎ A． B． ‎ C． D．‎ ‎17．福娃们在一起探讨研究下面的题目：‎ 函数（为常数）的图象如左图，‎ 如果时，；那么时，函数值（ ）‎ A． B． ‎ C． D．‎ x y O x1‎ x2‎ 参考下面福娃们的讨论，请你解该题，你选择的答案是（ ）‎ 贝贝：我注意到当时，．‎ 晶晶：我发现图象的对称轴为．‎ 欢欢：我判断出．‎ 迎迎：我认为关键要判断的符号．‎ 妮妮：可以取一个特殊的值．‎ 三、解答题：本大题共11小题，共81分．解答应写出必要的文字说明，证明步骤，推理过程．‎ ‎18．（本小题满分10分）计算化简 ‎（1）；‎ ‎（2）．‎ ‎19．（本小题满分10分）运算求解 解方程或不等式组 ‎（1）；‎ ‎（2）‎ ‎20．（本小题满分6分）实验探究 有两个黑布袋，布袋中有两个完全相同的小球，分别标有数字1和2．布袋中有三个完全相同的小球，分别标有数字，和．小明从布袋中随机取出一个小球，记录其标有的数字为，再从布袋中随机取出一个小球，记录其标有的数字为，这样就确定点的一个坐标为．‎ ‎（1）用列表或画树状图的方法写出点的所有可能坐标；‎ ‎（2）求点落在直线上的概率．‎ ‎21．（本小题满分6分）作图证明 A B C 如图，在中，作的平分线，交于，作线段的垂直平分线，分别交于，于，垂足为，连结．在所作图中，寻找一对全等三角形，并加以证明．（不写作法，保留作图痕迹）‎ ‎22．（本小题满分6分）推理运算 二次函数的图象经过点，，．‎ ‎（1）求此二次函数的关系式；‎ ‎（2）求此二次函数图象的顶点坐标；‎ ‎（3）填空：把二次函数的图象沿坐标轴方向最少平移 个单位，使得该图象的顶点在原点．‎ ‎23．（本小题满分6分）实际运用 ‎512汶川大地震发生以后，全国人民众志成城．首长到帐篷厂视察，布置赈灾生产任务，下面是首长与厂长的一段对话：‎ 首长：为了支援灾区人民，组织上要求你们完成12000顶帐篷的生产任务．‎ 厂长：为了尽快支援灾区人民，我们准备每天的生产量比原来多一半．‎ 首长：这样能提前几天完成任务？‎ 厂长：请首长放心！保证提前4天完成任务！‎ 根据两人对话，问该厂原来每天生产多少顶帐篷？‎ ‎24．（本小题满分6分）推理运算 如图，在直角坐标系中，直线与轴，轴分别交于两点，以为边在第二象限内作矩形，使．‎ ‎（1）求点，点的坐标，并求边的长；‎ x y O A B C D H ‎（2）过点作轴，垂足为，求证：；‎ ‎（3）求点的坐标．‎ ‎25．（本小题满分7分）实际运用 如图，奥运圣火抵达某市奥林匹克广场后，沿图中直角坐标系中的一段反比例函数图象传递．动点表示火炬位置，火炬从离北京路‎10米处的点开始传递，到离北京路‎1000米的点时传递活动结束．迎圣火临时指挥部设在坐标原点（北京路与奥运路的十字路口），为少先队员鲜花方阵，方阵始终保持矩形形状且面积恒为‎10000平方米（路线宽度均不计）．‎ ‎（1）求图中反比例函数的关系式（不需写出自变量的取值范围）；‎ ‎（2）当鲜花方阵的周长为500米时，确定此时火炬的位置（用坐标表示）；‎ ‎（3）设，用含的代数式表示火炬到指挥部的距离；当火炬离指挥部最近时，确定此时火炬的位置（用坐标表示）．‎ ‎（火炬）‎ y M x N A T B O 奥林匹克广场 北 京 路 鲜花 方阵 ‎（指挥部）‎ 奥运路 ‎26．（本小题满分7分）推理运算 如图，为直径，为弦，且，垂足为．‎ ‎（1）的平分线交于，连结．求证：为的中点；‎ ‎（2）如果的半径为，，‎ ‎①求到弦的距离；‎ ‎②填空：此时圆周上存在 个点到直线的距离为．‎ A B D E O C H ‎27．（本小题满分9分）理解发现 阅读以下材料：‎ 对于三个数，用表示这三个数的平均数，用表示这三个数中最小的数．例如：‎ ‎；；‎ 解决下列问题：‎ ‎（1）填空： ；‎ 如果，则的取值范围为．‎ ‎（2）①如果，求；‎ ‎②根据①，你发现了结论“如果，那么 （填的大小关系）”．证明你发现的结论；‎ ‎③运用②的结论，填空：‎ 若，‎ 则 ．‎ x y O ‎（3）在同一直角坐标系中作出函数，，的图象（不需列表描点）．通过观察图象，‎ 填空：的最大值为 ．‎ ‎28．（本小题满分8分）探索研究 x l Q C P A O B H R y 如图，在直角坐标系中，点为函数在第一象限内的图象上的任一点，点的坐标为，直线过且与轴平行，过作轴的平行线分别交轴，于，连结交轴于，直线交轴于．‎ ‎（1）求证：点为线段的中点；‎ ‎（2）求证：①四边形为平行四边形；‎ ‎②平行四边形为菱形；‎ ‎（3）除点外，直线与抛物线有无其它公共点？并说明理由．‎ 镇江市2008年初中毕业升学考试数学试卷 参考答案及评分标准 一、填空题：‎ ‎1．3，3 2．1，6 3．， 4．，‎ ‎5．， 6．3，3 7．65，35 8．4，12 ‎ ‎9．1，1 10．45，2 11． 12．‎ 二、填空题：‎ ‎13．B 14．A 15．D 16．C 17．C 三、解答题：‎ ‎18．（1）原式 （3分，每对1个得1分）‎ ‎． （5分）‎ ‎（2）原式 （1分）‎ ‎ （2分）‎ ‎ （4分）‎ ‎． （5分）‎ ‎19．（1）． （3分）‎ ‎，． （5分）‎ ‎（2）由①，得； （2分）‎ 由②，得． （4分）‎ 原不等式组的解集为． （5分）‎ ‎20．（1）用列表或画树状图的方法求点的坐标有，，，，，． （4分，列表或树状图正确得2分，点坐标2分）‎ ‎（2）“点落在直线上”记为事件，所以，‎ 即点落在直线上的概率为． （6分）‎ ‎21．（1）画角平分线，线段的垂直平分线． （3分，仅画出1条得2分）‎ ‎（2） （4分，只要1对即可），证明全等．（6分）‎ ‎22．（1）设， （1分）‎ 把点，代入得 （2分）‎ 解方程组得 ． （3分）‎ ‎（也可设）‎ ‎（2）． （4分）‎ 函数的顶点坐标为． （5分）‎ ‎（3）5 （6分）‎ ‎23．设该厂原来每天生产顶帐篷，根据题意得： （1分）‎ ‎． （3分）‎ 解方程得：． （4分）‎ 经检验：是原方程的根，且符合题意． （5分）‎ 答：该厂原来每天生产1000顶帐篷． （6分）‎ ‎24．（1），，‎ 在中，． （2分）‎ ‎（2）由，，‎ ‎，又，‎ ‎． （4分）‎ ‎（3），‎ ‎，即，‎ ‎，．‎ ‎． （6分）‎ ‎25．（1）设反比例函数为． （1分）‎ 则， （2分）‎ ‎． （3分）‎ ‎（2）设鲜花方阵的长为米，则宽为米，由题意得：‎ ‎． （4分）‎ 即：，‎ 解得：或，满足题意．‎ 此时火炬的坐标为或． （5分）‎ ‎（3），在中，‎ ‎． （6分）‎ 当时，最小，‎ 此时，又，，，‎ ‎，且．‎ ‎． （7分）‎ ‎26．（1）， （1分）‎ 又，．‎ ‎． （2分）‎ 又，．‎ 为的中点． （3分）‎ ‎（2）①，为的直径，，‎ ‎． （4分）‎ 又，．‎ ‎， （5分）‎ ‎．‎ 作于，则． （6分）‎ ‎②3 （7分）‎ ‎27．（1） （1分，填也得分）；‎ ‎ （2分）‎ ‎（2）①．‎ 法一：．‎ 当时，则，则，．‎ 当时，则，则，（舍去）．‎ 综上所述：． （4分）‎ 法二：，‎ ‎ （3分）‎ ‎ ． （4分）‎ ‎② （5分）‎ 证明：，‎ 如果，则，．‎ 则有，即．‎ ‎．‎ 又，．且．‎ ‎．‎ 其他情况同理可证，故． （6分）‎ ‎③ （7分）‎ ‎（3）作出图象．‎ x y O P ‎1‎ ‎ （8分）‎ ‎1 （9分）‎ ‎28．（1）法一：由题可知．‎ ‎，，‎ ‎． （1分）‎ ‎，即为的中点． （2分）‎ 法二：，，． （1分）‎ 又轴，． （2分）‎ ‎（2）①由（1）可知，，‎ ‎，，‎ ‎． （3分）‎ ‎，‎ 又，四边形为平行四边形． （4分）‎ ‎②设，轴，则，则．‎ 过作轴，垂足为，在中，‎ ‎．‎ 平行四边形为菱形． （6分）‎ ‎（3）设直线为，由，得，代入得：‎ ‎ 直线为． （7分）‎ 设直线与抛物线的公共点为，代入直线关系式得：‎ ‎，，解得．得公共点为．‎ 所以直线与抛物线只有一个公共点． （8分）‎