2011黑龙江龙东中考数学试题及答案

2011黑龙江龙东中考数学试题及答案

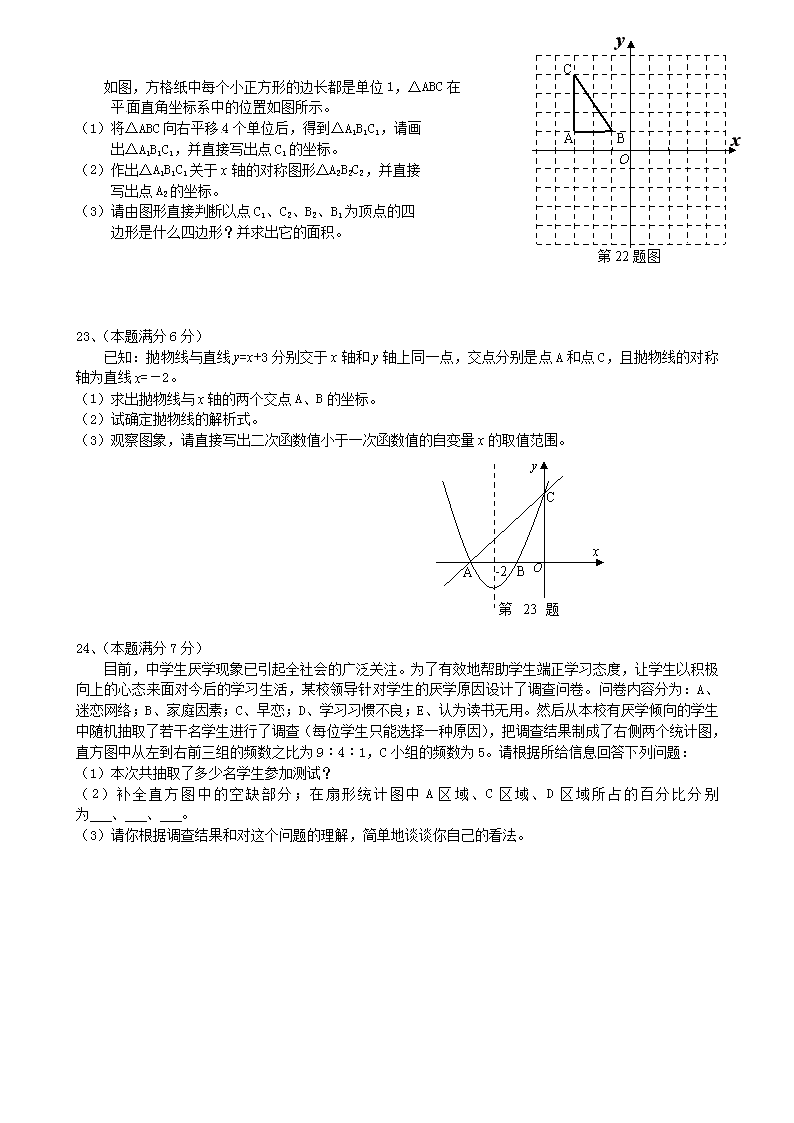
‎ 黑龙江省龙东地区2011年初中毕业学业 统一考试 数 学 试 题 本考场试卷序号 ‎（ 由监考填写）‎ 考生注意：‎ ‎1、考试时间120分钟 ‎ ‎2、全卷共三道大题，总分120分 题号 一 二 三 总 分 核分人 ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ ‎26‎ ‎27‎ ‎28‎ 得分 一、填空题（每题3分，满分30分）‎ 1、 国家统计局新闻发言人盛来运‎2010年7月15日在国新办的新闻发布会上宣布，据初步测算，上半年国内生产总值是172840亿元，比上年同期增长了3.7个百分点。数据172840亿元用科学记数法表示为 亿元（结果保留三个有效数字）。‎ ‎2、函数y=中，自变量x的取值范围是 。‎ ‎3、如图所示，正方形ABCD中，点E在BC上，点F在DC上，请添加一个条件： ，使△ABE≌△BCF（只添一个条件即可）。‎ ‎4、抛物线y=－(x+1)2－1的顶点坐标为 。 ‎ ‎5、已知等腰三角形两边长分别为5和8，则底角的余弦值为 。‎ ‎6、已知扇形的圆心角为60°，圆心角所对的弦长是‎2cm，则此扇形的面积为 cm2。‎ ‎7、我市为了增强学生体质，开展了乒乓球比赛活动。部分同学进入了半决赛，赛制为单循环形式（即每两个选手之间都赛一场），半决赛共进行了6场，则共有 人进入半决赛。‎ 第3题图 A D C B F E ‎ A 第8题图 C B 第10题图 A D C B A1‎ B1‎ C1‎ D1‎ A2‎ B2‎ C2‎ D2‎ A3‎ B3‎ C3‎ D3‎ ‎ ‎8、如图，已知⊙O的半径为4，OC垂直弦AB于点C，∠AOB=120°，则弦AB长为 。‎ ‎9、已知关于x的分式方程－=0无解，则a的值为 。‎ ‎10、如图，四边形ABCD中，对角线AC⊥BD，且AC=8，BD=4，各边中点分别为A1、B1、C1、D1，顺次连接得到四边形A1B‎1C1D1，再取各边中点A2、B2、C2、D2，顺次连接得到四边形A2B‎2C2D2，……，依此类推，这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为 。‎ 二、选择题（每题3分，满分30分）‎ ‎11、下列各运算中，计算正确的个数是 （ ）‎ ‎①3x2+5x2=8x4 ② (－m2n)2=m4n2 ③ (－)－2=16 ④－= ‎ A、1 B、‎2 C、3 D、4‎ ‎12、下列QQ标识图形中既是轴对称图形又是中心对称图形的是 （ ）‎ ‎① ② ③ ④ ⑤ ⑥‎ A、①③⑤ B、③④⑤ C、②⑥ D、④⑤⑥‎ ‎13、某校九年级有11名同学参加数学竞赛，预赛成绩各不相同，要取前5名参加决赛。小兰已经知道了自已的成绩，她想知道自已能否进入决赛，还需要知道这11名同学成绩的 （ ） ‎ ‎ A、中位数 B、众数 C、平均数 D、不能确定 ‎14、已知：力F所作的功是15焦（功=力×物体在力的方向上通过的距离），则力F与物体在力的方向上通过的距离S之间的函数关系图象大致是下图中的 （ ）‎ E A D C B F H G P 第15题图 F S F S F S F S A D C B ‎15、如图，在平行四边形ABCD中，过对角线BD上一点P作EF∥AB，GH∥AD，与各边交点分别为E、F、G、H，则图中面积相等的平行四边形的对数为 （ ） ‎ A、3 B、‎4 C、5 D、6‎ ‎16、当1＜a＜2时，代数式︱a－2︱+︱1－a︱的值是 （ ）‎ ‎ A、－1 B、‎1 ‎ C、3 D、－3‎ ‎17、在一个口袋中有4个完全相同的小球，把它们分别标号为 1，2，3，4，随机地摸出一个小球然后放回，再随机地摸出一个小球。则两次摸出的小球的标号的和等于6的概率为（ ）‎ ‎ A、 B、 C、 D、‎ ‎18、在△ABC中，BC:AC:AB=1:1:，则△ABC是 （ ）‎ ‎ A、等腰三角形 B、钝角三角形 C、直角三角形 D、等腰直角三角形 ‎ A P C B M 第20题图 N ‎19、把一些笔记本分给几个学生，如果每人分3本，那么余8本；如果前面的每个学生分5本，那么最后一人就分不到3本。则共有学生 （ ）‎ A、4人 B、5人 C、6人 D、5人或6人 ‎20、在锐角△ABC中，∠BAC=60°，BN、CM为高，P为BC的中点，连接MN、MP、NP，‎ 则结论：①NP=MP ②当∠ABC=60°时，MN∥BC ③ BN=2AN ④AN︰AB=AM︰AC，一定 正确的有 （ ） ‎ A、1个 B、2个 C、3个 D、4个 ‎ 三、解答题（满分60分）‎ ‎21、（本题满分5分）‎ 先化简，再求值:÷（2x — ）其中，x=+1 ‎ ‎22、（本题满分6分）‎ x 第22题图 A B C O y 如图，方格纸中每个小正方形的边长都是单位1，△ABC在 平面直角坐标系中的位置如图所示。‎ ‎（1）将△ABC向右平移4个单位后，得到△A1B‎1C1，请画 出△A1B‎1C1，并直接写出点C1的坐标。‎ ‎（2）作出△A1B‎1C1关于x轴的对称图形△A2B‎2C2，并直接 写出点A2的坐标。‎ ‎（3）请由图形直接判断以点C1、C2、B2、B1为顶点的四 边形是什么四边形？并求出它的面积。‎ ‎ ‎ ‎23、（本题满分6分）‎ 已知：抛物线与直线y=x+3分别交于x轴和y轴上同一点，交点分别是点A和点C，且抛物线的对称轴为直线x=－2。‎ ‎（1）求出抛物线与x轴的两个交点A、B的坐标。‎ ‎（2）试确定抛物线的解析式。‎ ‎（3）观察图象，请直接写出二次函数值小于一次函数值的自变量x的取值范围。‎ 第23题图 A C B ‎-2‎ ‎ ‎ ‎24、（本题满分7分）‎ 目前，中学生厌学现象已引起全社会的广泛关注。为了有效地帮助学生端正学习态度，让学生以积极向上的心态来面对今后的学习生活，某校领导针对学生的厌学原因设计了调查问卷。问卷内容分为：A、迷恋网络；B、家庭因素；C、早恋；D、学习习惯不良；E、认为读书无用。然后从本校有厌学倾向的学生中随机抽取了若干名学生进行了调查（每位学生只能选择一种原因），把调查结果制成了右侧两个统计图，直方图中从左到右前三组的频数之比为9︰4︰1，C小组的频数为5。请根据所给信息回答下列问题：‎ ‎（1）本次共抽取了多少名学生参加测试？‎ ‎（2）补全直方图中的空缺部分；在扇形统计图中A区域、C区域、D区域所占的百分比分别为 、 、 。‎ ‎（3）请你根据调查结果和对这个问题的理解，简单地谈谈你自己的看法。‎ 第24题 图二 频数(人)‎ A ‎ ‎5E ‎105E ‎30‎ ‎40‎ 小组 第24题 图一 B ‎ C ‎ D ‎ E ‎ ‎0 ‎ D C A B ‎180‎ E ‎1‎ ‎（ ） （ ）‎ F ‎3‎ ‎（小时）‎ ‎（ ）‎ ‎（千米）‎ 甲车 乙车 第25题图 ‎25、（本题满分8分） ‎ 汶川灾后重建工作受到全社会的广泛关注，全国各省对口支援四川省受灾市县。我省援建剑阁县，建筑物资先用火车源源不断的运往距离剑阁县‎180千米的汉中市火车站，再由汽车运往剑阁县。甲车在驶往剑阁县的途中突发故障，司机马上通报剑阁县总部并立即检查和维修。剑阁县总部在接到通知后第12分钟时，立即派出乙车前往接应。经过抢修，甲车在乙车出发第8分钟时修复并继续按原速行驶，两车在途中相遇。为了确保物资能准时运到，随行人员将物资全部转移到乙车上（装卸货物时间和乙车掉头时间忽略不计），乙车按原速原路返回，并按预计时间准时到达剑阁县。下图是甲、乙两车离剑阁县的距离y（千米）与时间x（小时）之间的函数图象。请结合图象信息解答下列问题：‎ ‎（1）请直接在坐标系中的( )内填上数据。‎ ‎（2）求直线CD的函数解析式，并写出自变量的取值范围。‎ ‎（3）求乙车的行驶速度。‎ ‎26、（本题满分8分）‎ 如图，点E是矩形ABCD的对角线BD上的一点，且BE=BC，AB=3，BC=4，点P为直线EC上的一点，且PQ⊥BC于点Q，PR⊥BD于点R。‎ ‎（1）如图1，当点P为线段EC中点时，易证：PR+PQ=（不需证明）。‎ ‎（2）如图2，当点P为线段EC上的任意一点（不与点E、点C重合）时，其它条件不变，则（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由。‎ ‎（3）如图3，当点P为线段EC延长线上的任意一点时，其它条件不变，则PR与PQ之间又具有怎样的数量关系？请直接写出你的猜想。‎ 第26题图1‎ A D C B Q R E P 第26题图2‎ A D C B Q R E P A D C B Q R E P 第26题图3‎ ‎ ‎ ‎27、（本题满分10分）‎ ‎2010年6月5日是第38个世界环境日，世界环境日的主题为“多个物种、一颗星球、一个未来”。为了响应节能减排的号召，某品牌汽车4S店准备购进A型（电动汽车）和B型（太阳能汽车）两种不同型号的汽车共16辆，以满足广大支持环保的购车者的需求。市场营销人员经过市场调查得到如下信息：‎ 成本价（万元/辆）‎ 售价（万元/辆）‎ A型 ‎30‎ ‎32‎ B型 ‎42‎ ‎45‎ ‎（1）若经营者的购买资金不少于576万元且不多于600万元，则有哪几种进车方案？‎ ‎（2）在（1）的前提下，如果你是经营者，并且所进的汽车能全部售出，你会选择哪种进车方案才能使获得的利润最大？最大利润是多少？‎ ‎（3）假设每台电动汽车每公里的用电费用为0.65元，且两种汽车最大行驶里程均为30万公里，那么从节约资金的角度，你做为一名购车者，将会选购哪一种型号的汽车？并说明理由。‎ ‎28、（本题满分10分）‎ 如图，直线AB与坐标轴分别交于点A、点B，且OA、OB的长分别为方程x2－6x+8=0的两个根（OA＜OB），点C在y轴上，且 OA︰AC=2︰5，直线CD垂直于直线AB于点P，交x轴于点D。‎ ‎（1）求出点A、点B的坐标。‎ ‎（2）请求出直线CD的解析式。 ‎ ‎（3）若点M为坐标平面内任意一点，在坐标平面内是否存在这样的点M，使以点B、P、D、M为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由。‎ A C B D P ‎ 第28题图 数学试题参考答案及评分标准 一、填空题（每题3分）‎ ‎1、1.73×105 ‎ ‎ 2、x＞0 ‎ ‎ 3、BE=CF（或CE=DF或AE=BF或∠BAE=∠CBF或∠AEB=∠BFC或BF⊥AE等）‎ ‎4、（－1，－1） ‎ ‎ 5、或 （答对1个得2分，答对2个得3分）‎ ‎ 6、π ‎ ‎ 7、4 ‎ ‎ 8、4 ‎ ‎ 9、－1或0或（每个答案1分）‎ ‎10、（或或，只要答案正确即可）‎ 二、单项选择题（每题3分）‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ B D A B A B C D C C ‎21、（本题满分5分）‎ 解：原式=÷………………………………………………..1分 ‎ =·………………………………………….2分 ‎ =……………………………………………………………………..1分 当x=+1时，原式=＝=…………………………1分 ‎22、（本题满分6分）‎ 解：（1）正确画出向右平移4个单位的图形……………………………………………..1分 ‎ C1（1，4）．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分 ‎（2）正确画出图形．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分 ‎ A2（1，－1）…………………………………………………．．．．．．．．………….1分 ‎（3）四边形C‎1C2B2B1是等腰梯形．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎　　由图可得：Ｂ１Ｂ２＝２，Ｃ１Ｃ２＝８，A1B1=2‎ ‎∴梯形的面积===10．．．．．．．．．．．．．．．．．．．１分 ‎23、（本题满分6分）‎ 解：（1）y=x+3中，‎ 当y=0时, x=3‎ ‎ ∴点A的坐标为(－3,0)．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ 当x=0时,y=3‎ ‎ ∴点C坐标为（0，3）‎ ‎ ∵抛物线的对称轴为直线x=－2‎ ‎ ∴点A与点B关于直线x=－2对称 ‎ ∴点B的坐标是（-1，0）．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎（2）设二次函数的解析式为y=ax2+bx+c ‎∵二次函数的图象经过点C（0，3）和点A(－3,0)，且对称轴是直线x=－2‎ ‎∴可列得方程组： C=3 ‎ ‎ ‎9a－3b+c=0 ‎ ‎ －=－2．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ 解得： a=1 ‎ b=4‎ c=3‎ ‎∴二次函数的解析式为y=x2+4x+3．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎（或将点A、点B、点C的坐标依次代入解析式中求出a、b、c的值也可）‎ ‎（3）由图象观察可知，当－3＜x＜0时,二次函数值小于一次函数值。．．．．．．．．．２分 ‎24、（本题满分7分）‎ 解：（1）∵C小组的人数为5人，占被抽取人数的20%，且前三组的频数之比为9：4：1‎ ‎∴5×4÷20%=100（人）‎ ‎ ∴本次抽取的人数为100。．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．2分 ‎ （2）A：45% C：5% D：12% ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分 ‎ 补全直方图的高度为12……………………………………………………………1分 ‎（3）看法积极向上均可………………………………………………………………….1分 ‎25、（本题满分8分）‎ 解：（1）纵轴填空为：120 横轴从左到右依次填空为：1.2 ；2.1．．．．．．．．．．3分 ‎ （2）作DK⊥X轴于点K ‎ 由（1）可得K点的坐标为（2.1，0）‎ ‎ 由题意得： 120－（2.1－1－）×60=74‎ ‎ ∴点D坐标为（2.1，74）．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ 设直线CD的解析式为y=kx+b ‎ ∵C（，120），D（2.1，74）‎ ‎ ∴ K+b=120‎ ‎ 2.1k+b=74‎ ‎ 解得： k=－60‎ ‎ b=200．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ ∴直线ＣＤ的解析式为：yCD=－60X+200(≤X≤2.1)．．．．．．．．．．．．．．．．．．．１分 ‎ （3）由题意得：V乙=74÷（3－2.1）=（千米/时）‎ ‎ ∴乙车的速度为（千米/时）．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．２分 ‎26、（本题满分8分）‎ 解：(2) 图2中结论PR+PQ=仍成立。．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．.2分 证明:连接BP, 过C点作CK⊥BD于点K。‎ ‎∵四边形ABCD为矩形 ‎∴∠BCD=90°‎ 又∵CD=AB=3,BC=4‎ ‎∴BD===5‎ ‎∵S△BCD=BC·CD=BD·CK ‎∴3×4=5CK ‎∴CK=．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分 ‎∵S△BCE=BE·CK, S△BEP=PR·BE, S△BCP =PQ·BC且 S△BCE= S△BEP+ S△BCP ‎∴BE·CK=PR·BE+PQ·BC．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 又∵BE=BC ‎∴CK=PR+PQ ‎∴CK=PR+PQ 又∵CK=‎ ‎∴PR+PQ=．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．2分 ‎（除此方法外，只要证明方法准确、合理均可得分）‎ ‎(3) 图3中的结论是PR－PQ=．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．２分 ‎27、（本题满分10分）‎ 解：设A型汽车购进x辆，则B型汽车购进（16－x）辆。‎ 根据题意得： 30x+42(16－x)≤600‎ ‎ 30x+42(16－x)≥576．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．２分 解得：６≤x≤8．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎∵x为整数 ‎∴x取6、7、8。‎ ‎∴有三种购进方案：‎ A型 ‎6辆 ‎7辆 ‎8辆 B型 ‎10辆 ‎9辆 ‎8辆 ‎．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ ‎（２）设总利润为w万元，‎ 根据题意得：W=(32－30)x+(45－42)(16－x)．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ 　 =－x+48‎ ‎∵－1＜0‎ ‎∴w随x的增大而减小．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎∴当x=6时，w有最大值，w最大=－6+48=42（万元）．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ ∴当购进A型车６辆，B型车10辆时，可获得最大利润，最大利润是４２万元。．．．１分 ‎（3）设电动汽车行驶的里程为a万公里。‎ ‎ 当3２+‎0.65a=4５时，a=２０＜30．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分 ‎ ∴选购太阳能汽车比较合算。．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分 ‎ 28、（本题满分10分）‎ ‎ 解：∵x2－6x+8=0‎ ‎ ∴x1=4,x2=2．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ ∵‎0A、0B为方程的两个根，且‎0A＜0B ‎ ∴‎0A=2，0B=4．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ ∴ A(0,2)，B(－4,0)．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ ∵ ‎0A:AC=2:5‎ ‎ ∴ AC=5‎ ‎ ∴OC=OA+AC=2+5=7‎ ‎ ∴ C(0,7)．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ ∵∠BAO=∠CAP,∠CPB=∠BOA=90O ‎ ∴∠PBD=∠OCD ‎ ∵∠ BOA=∠COD=90O ‎ ∴△BOA∽△COD ‎ ∴=‎ ‎ ∴ OD===．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ ∴D(,0)‎ ‎ 设直线 CD的解析式为y=KX+b 把x=0,y=7;x=,y=0分别代入得：‎ ‎ b=7‎ ‎ k+b=0‎ ‎ b=7‎ ‎ ∴ k =－2．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ ∴yCD=－2x+7．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１分 ‎ (3)存在，P1(－5.5 , 3) ,P2(9.5 , 3) ,P3(－2.5 , －3)．．．．．．．．．．．．３分