压轴题中考数学压轴题精选精析例
2012中考数学压轴题精选精析(41-50例)
(右侧加有批注)
2011安徽八、(本题满分14分)
A
B
C
D
l1
l2
l3
l4
h1
h2
h3
23.如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3(h1>0,h2>0,h3>0).
(1)求证:h1=h2;
【证】
(2)设正方形ABCD的面积为S,求证:S=(h1+h2)2+h12;
【证】
(3)若h1+h2=1,当h1变化时,说明正方形ABCD的面积S随h1的变化情况.
【解】
23.(1)过A点作AF⊥l3分别交l2、l3于点E、F,过C点作CH⊥l2分别交l2、l3于点H、G,证△ABE≌△CDG即可.
(2)易证△ABE≌△BCH≌△CDG≌△DAF,且两直角边长分别为h1、h1+h2,四边形EFGH是边长为h2的正方形,
所以.
(3)由题意,得 所以
又 解得0<h1<
∴当0<h1<时,S随h1的增大而减小;
当h1=时,S取得最小值;
当<h1<时,S随h1的增大而增大.
2011芜湖24.(本小题满分14分)
平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、(,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形。
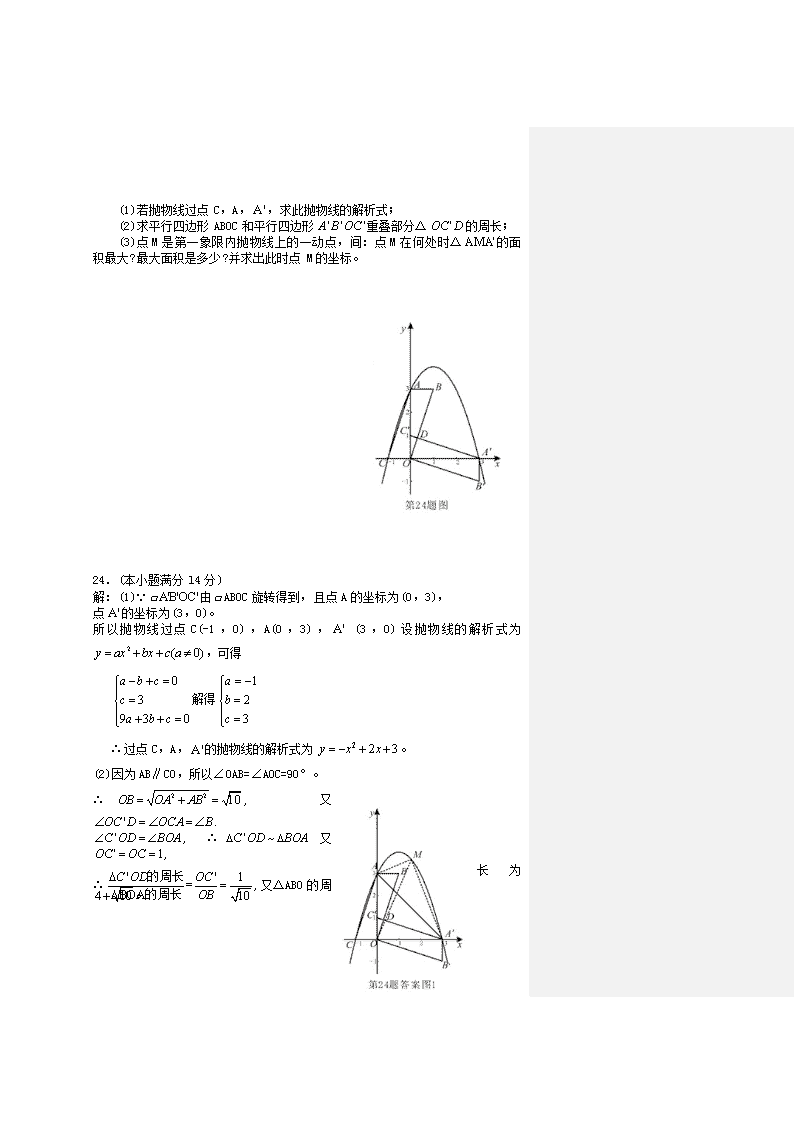
(1)若抛物线过点C,A,,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形重叠部分△的周长;
(3)点M是第一象限内抛物线上的一动点,间:点M在何处时△的面积最大?最大面积是多少?并求出此时点M的坐标。
24.(本小题满分l4分)
解:(1)∵由ABOC旋转得到,且点A的坐标为(0,3),
点的坐标为(3,0)。
所以抛物线过点C(-1,0),A(0,3), (3,0)设抛物线的解析式为,可得
解得
∴过点C,A,的抛物线的解析式为。
(2)因为AB∥CO,所以∠OAB=∠AOC=90°。
∴,又.
,∴ 又,
∴,又△ABO的周长为。
∴的周长为。
(3)连接OM,设M点的坐标为,
∵点M在抛物线上,∴。
∴
=
=
因为,所以当时,。△AMA’的面积有最大值
所以当点M的坐标为()时,△AMA’的面积有最大值,且最大值为。
(2011上海)25.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)
在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN,.
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出函数的定义域;
(3)若△AME∽△ENB(△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应),求AP的长.
图1 图2 备用图
25. (本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)
(1) 由AE=40,BC=30,AB=50,ÞCP=24,又sinÐEMP=ÞCM=26.
(2) 在Rt△AEP与Rt△ABC中,∵ ÐEAP=ÐBAC,∴ Rt△AEP ~ Rt△ABC,
∴ ,即,∴ EP=x,
又sinÐEMP=ÞtgÐEMP==Þ=,∴ MP=x=PN,学科王
BN=AB-AP-PN=50-x-x=50-x (0
2,AP>2;因此以1、2、3、4为边或以2、3、4、5为边都不符合题意,所以四条边的长只能是3、4、5、6的一种情况,在Rt△AOM中,,因为抛物线对称轴过点M,所以在抛物线的图象上有关于点A的对称点与M的距离为5,即PM=5,此时点P横坐标为6,即AP=6;故以A、O、M、P为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立,
即P(6,4).···································5分
(注:如果考生直接写出答案P(6,4),给满分2分,但考生答案错误,解答过程分析合理可酌情给1分)
⑶法一:在直线AC的下方的抛物线上存在点N,使△NAC面积最大.
设N点的横坐标为,此时点N(,过点N作NG∥轴交AC于G;由点A(0,4)和点C(5,0)可求出直线AC的解析式为:
;把代入得:,则G,
此时:NG=-(),
=. ······································7分
∴
∴当时,△CAN面积的最大值为,
由,得:,∴N(, -3). ········ 8分
法二:提示:过点N作轴的平行线交轴于点E,作CF⊥EN于点F,则
(再设出点N的坐标,同样可求,余下过程略)
(2011年凉山州)如图,抛物线与轴交于(,0)、(,0)两点,且,与轴交于点,其中是方程的两个根。
(1)求抛物线的解析式;
(2)点是线段上的一个动点,过点作∥,交于点,连接,当的面积最大时,求点的坐标;
(3)点在(1)中抛物线上,点为抛物线上一动点,在轴上是否存在点,使以为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点的坐标,若不存在,请说明理由。
y
x
O
B
M
N
C
A
28题图
28.(1)∵,∴,。
∴,。····················1分
又∵抛物线过点、、,
故设抛物线的解析式为,
将点的坐标代入,求得。
∴抛物线的解析式为。········3分
(2)设点的坐标为(,0),过点作轴于点(如图(1))。
∵点的坐标为(,0),点的坐标为(6,0),
∴,。···························4分
∵,∴。
∴,∴,∴。·················5分
y
x
O
B
E
A
图(2)
D
∴
······6分
。
∴当时,有最大值4。
此时,点的坐标为(2,0)。··············7分
(3)∵点(4,)在抛物线上,
y
x
O
B
A
图(3)
D
∴当时,,
∴点的坐标是(4,)。
如图(2),当为平行四边形的边时,,
∵(4,),∴(0,),。
∴,。 ··········9分
① 如图(3),当为平行四边形的对角线时,
设,则平行四边形的对称中心为
(,0)。·················10分
∴的坐标为(,4)。
把(,4)代入,得。
解得 。
,。····
(株洲市2011年)24.(本题满分10分)孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点,两直角边与该抛物线交于、两点,请解答以下问题:
(1)若测得(如图1),求的值;
(2)对同一条抛物线,孔明将三角板绕点旋转到如图2所示位置时,过作轴于点,测得,写出此时点的坐标,并求点的横坐标;
(3)对该抛物线,孔明将三角板绕点旋转任意角度时惊奇地发现,交点、的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
图1
图2
24.解:
(1)设线段与轴的交点为,由抛物线的对称性可得为中点,
,,
,(,) ……… 2分
将(,)代入抛物线得,. ……… 3分
(2)解法一:过点作轴于点,
点的横坐标为, (1,), ……… 4分
. 又 ,易知,又,
△∽△, ……… 5分
设点(,)(),则,,
,即点的横坐标为. ……… 6分
解法二:过点作轴于点,
点的横坐标为, (1,), ……… 4分
,易知,
, ……… 5分
设点(-,)(),则,,
,即点的横坐标为. ……… 6分
解法三:过点作轴于点,
点的横坐标为, (1,), ……… 4分
设(-,)(),则
,,,
,
,
解得:,即点的横坐标为. ……… 6分
(3)解法一:设(,)(),(,)(),
设直线的解析式为:, 则,……… 7分
得,,
……… 8分
又易知△∽△,,,……… 9分
.由此可知不论为何值,直线恒过点(,)………10分
(说明:写出定点的坐标就给2分)
解法二:设(,)(),(,)(),
直线与轴的交点为,根据,可得
,
化简,得. ……… 8分
又易知△∽△,,,……… 9分为固定值.故直线恒过其与轴的交点(,)……… 10分
说明:的值也可以通过以下方法求得.
由前可知,,,,
由,得:,
化简,得.
本答案仅供参考,若有其他解法,请参照本评分标准
(2011年桂林市)26.(本题满分12分)已知二次函数的图象如图.
(1)求它的对称轴与轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与轴,轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
26.(本题满分12分)
解: (1)由得 …………1分
∴D(3,0)…………2分
(2)方法一:
如图1, 设平移后的抛物线的解析式为
…………3分
则C OC=
令 即
得 …………4分
∴A,B
∴………5分
……………………6分
∵
即:
得 (舍去) ……………7分
∴抛物线的解析式为 ……………8分
方法二:
∵ ∴顶点坐标
设抛物线向上平移h个单位,则得到,顶点坐标…………3分
∴平移后的抛物线: ……………………4分
当时, , 得
∴ A B……………………5分
∵∠ACB=90° ∴△AOC∽△COB
∴OA·OB……………………6分
得 ,…………7分
∴平移后的抛物线: …………8分
(3)方法一:
如图2, 由抛物线的解析式可得
A(-2 ,0),B(8,0) ,C(4,0) ,M …………9分
过C、M作直线,连结CD,过M作MH垂直y轴于H,
则
∴
在Rt△COD中,CD==AD
∴点C在⊙D上 …………………10分
∵
……11分
∴
∴△CDM是直角三角形,∴CD⊥CM
∴直线CM与⊙D相切 …………12分
方法二:
如图3, 由抛物线的解析式可得
A(-2 ,0),B(8,0) ,C(4,0) ,M …………9分
作直线CM,过D作DE⊥CM于E, 过M作MH垂直y轴于H,则, , 由勾股定理得
∵DM∥OC
∴∠MCH=∠EMD
∴Rt△CMH∽Rt△DME …………10分
∴ 得 …………11分
由(2)知 ∴⊙D的半径为5
∴直线CM与⊙D相切 …………12分
(达州市2011年)23、(10分)如图,已知抛物线与轴交于A (1,0),B(,0)两点,与轴交于点C(0,3),抛物线的顶点为P,连结AC.
(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,且直线DC与轴交于点Q,求点D的坐标;
(3)抛物线对称轴上是否存在一点M,使得S△MAP=2S△ACP,若存在,求出M点坐标;若不存在,请说明理由.
23、(10分)解(1)设此抛物线的解析式为:
∵抛物线与轴交于A(1,0)、B(两点,
∴
又∵抛物线与轴交于点C(0,3)
∴,
∴
∴
即……………3分
用其他解法参照给分
(2)∵点A(1,0),点C(0,3)
∴OA=1,OC=3,
∵DC⊥AC,OC⊥轴
∴△QOC∽△COA
∴,即
∴OQ=9,……………………4分
又∵点Q在轴的负半轴上,∴Q(
设直线DC的解析式为:,则
解之得:
∴直线DC的解析式为:……………………5分
∵点D是抛物线与直线DC的交点,
∴ 解之得: (不合题意,应舍去)
∴点D(……………………6分
用其他解法参照给分
(3)如图,点M为直线上一点,连结AM,PC,PA
设点M(,直线与轴交于点E,∴AE=2
∵抛物线的顶点为P,对称轴为
∴P(
∴PE=4
则PM=
∵S四边形AEPC=S四边形OEPC+S△AOC
=
=
=……………………7分
又∵S四边形AEPC= S△AEP+S△ACP
S△AEP=
∴+S△ACP=……………………8分
∵S△MAP=2S△ACP
∴
∴
∴,……………………9分
故抛物线的对称轴上存在点M使S△MAP=2S△ACP
点M(或……………………10分
用其他解法参照给分