上海市青浦区中考数学二模卷及答案无水印

上海市青浦区中考数学二模卷及答案无水印

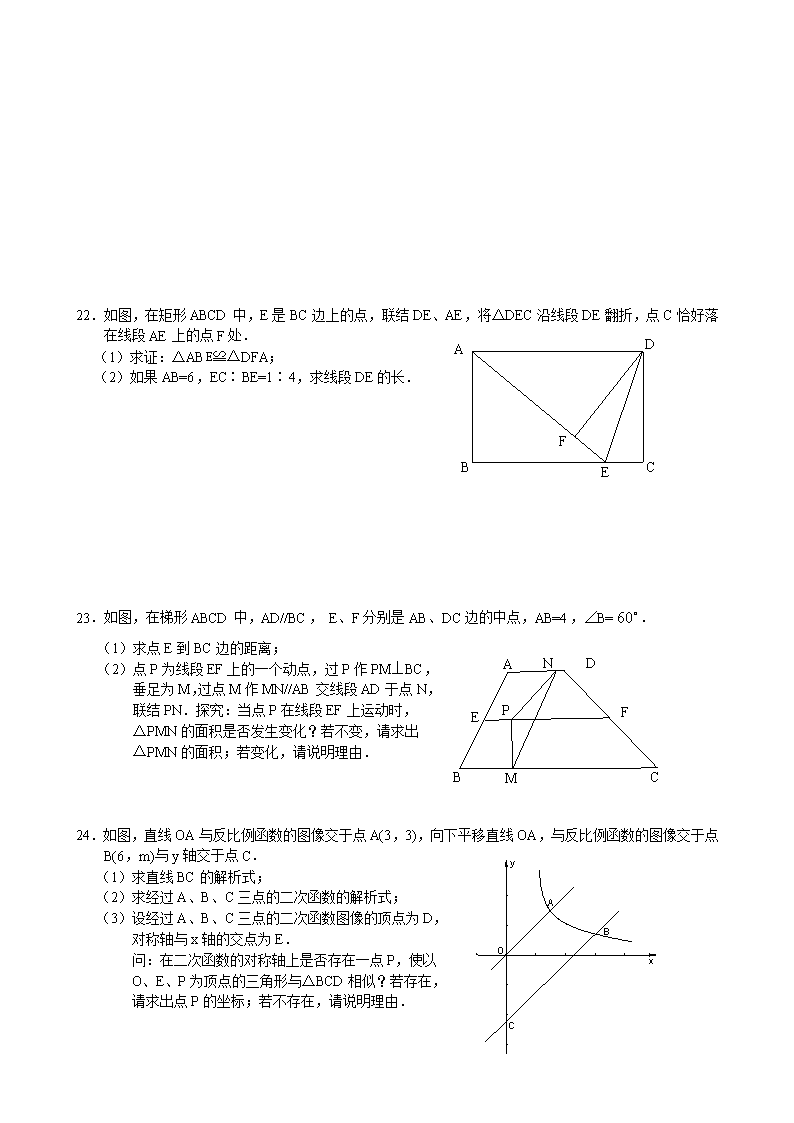
‎2010年青浦区初中学业模拟考试 ‎　　　　　 数 学 试 卷　　　 Q.2010.4‎ ‎ （满分150分，考试时间100分钟）‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎[每小题只有一个正确选项，在答题纸的相应题号的选项上用2 B铅笔填涂]‎ ‎1．下列运算正确的是………………………………………………………………………（ ）‎ ‎（A）； （B）； ‎ ‎（C）； （D）．‎ ‎2．与是同类二次根式的是……………………………………………………………（ ）‎ ‎（A）； （B）； （C）； （D）．‎ ‎3．在样本方差的计算式中，数字5和10分别表示样本的………………………………………………………………………………（ ）‎ ‎（A）容量，方差； （B）平均数，众数； ‎ ‎（C）标准差，平均数； （D）容量，平均数．‎ ‎4．边长为2的正六边形的边心距为………………………………………………………（ ）‎ ‎（A）1； （B）2； （C）； （D）2． ‎ ‎5．下列命题中真命题是……………………………………………………………………（ ）‎ ‎（A）有一组邻边相等的四边形是菱形； （B）四条边都相等的四边形是菱形； ‎ ‎（C）对角线互相垂直的四边形是菱形； （D）对角线互相平分且相等的四边形是菱形．‎ ‎6．如图，图案⑥是由①②③④⑤五种基本图形中的两种拼接而成的，这两种基本图形是（ ）‎ ‎（A）①⑤； （B）②⑤； （C）③⑤； （D）②④．‎ ‎ ‎ ‎① ② ③ ④ ⑤ ⑥‎ 二、填空题： （本大题共12题，每题4分，满分48分）‎ ‎7．计算： ．‎ ‎8．不等式的解集是 ．‎ ‎9．函数的定义域是 ． ‎ ‎10．方程的解是 ． ‎ ‎11．因式分解：．‎ ‎12．如果关于x的一元二次方程有两个不相等的实数根，那么实数k的取值范围是 ．‎ ‎13．直角坐标平面内，直线一定不经过第____________象限．‎ ‎14．从1、2、3、4、5、6这六个数中任意取出一个数，取到的数能够被2整除的概率是 ．‎ ‎15．某人在斜坡上走了‎26米，上升的高度为‎10米，那么这个斜坡的坡度 ．‎ E D C B A ‎16．如右图，点D、E分别在△ABC的AB、AC边上，DE∥BC，且，若，，‎ 用、表示，则 ．‎ ‎17．在□ABCD中，AC与BD相交于点O，点E是AB的中点，△ACD 的周长为20，则△AOE的周长为 ．‎ ‎18．在△ABC中，AB=AC，∠A=80°，将△ABC绕着点B旋转，使点 A落在直线BC上，点C落在点，则∠= ．‎ 三、解答题：（本大题共7题，满分78分，第19-22题每题10分，第23-24题每题12分，第25题14分）‎ ‎19．先化简，再求值：，其中．‎ ‎⑴‎ ‎⑵‎ ‎20．解方程组：‎ ‎21．某中学举行了一次“世博”知识竞赛，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分都是正整数，满分为100分）进行统计．请你根据下面局部尚未完成的频率分布表和频率分布直方图解答下列问题：‎ ‎（1）频率分布表中的a=__________，b=__________；‎ ‎（2）补全频率分布直方图；‎ ‎（3）在该问题的样本中,样本中位数落在_____________组内； ‎ ‎（4）若成绩在90分以上（不含90分）为优秀，则该校参加这次竞赛成绩优秀的约有______人．‎ 频率分布直方图：‎ ‎0.08‎ ‎0.20‎ ‎0.32‎ ‎ ‎ ‎ 频率分布表：‎ 分组 频数 频率 ‎50.5—60.5‎ ‎4‎ ‎0.08‎ ‎60.5—70.5‎ a ‎0.16‎ ‎70.5—80.5‎ ‎10‎ ‎0.20‎ ‎80.5—90.5‎ ‎16‎ ‎0.32‎ ‎90.5—100.5‎ ‎12‎ b D A B C E F ‎22．如图，在矩形ABCD中，E是BC边上的点，联结DE、AE，将△DEC沿线段DE翻折，点C恰好落在线段AE上的点F处．‎ ‎（1）求证：△ABE≌△DFA； ‎ ‎（2）如果AB=6，EC∶BE=1∶4，求线段DE的长．‎ ‎23．如图，在梯形ABCD中，AD//BC， E、F分别是AB、DC边的中点，AB=4，∠B=．‎ A D N P E F M B C ‎（1）求点E到BC边的距离；‎ ‎（2）点P为线段EF上的一个动点，过P作PM⊥BC，‎ 垂足为M，过点M作MN//AB交线段AD于点N，‎ 联结PN．探究：当点P在线段EF上运动时，‎ ‎△PMN的面积是否发生变化？若不变，请求出 ‎△PMN的面积；若变化，请说明理由．‎ O A B C y x ‎24．如图，直线OA与反比例函数的图像交于点A(3，3)，向下平移直线OA，与反比例函数的图像交于点B(6，m)与y轴交于点C．‎ ‎ （1）求直线BC的解析式；‎ ‎ （2）求经过A、B、C三点的二次函数的解析式；‎ ‎ （3）设经过A、B、C三点的二次函数图像的顶点为D，‎ 对称轴与x轴的交点为E．‎ 问：在二次函数的对称轴上是否存在一点P，使以 O、E、P为顶点的三角形与△BCD相似？若存在，‎ 请求出点P的坐标；若不存在，请说明理由．‎ ‎25．如图，已知△ABC中，AB=AC=，BC=4，点O在BC边上运动，以O为圆心，OA为半径的圆与边AB交于点D（点A除外），设OB，AD ．‎ ‎（1）求的值；‎ ‎（2）求关于的函数解析式，并写出函数的定义域；‎ C O D B A ‎（3）当点O在BC边上运动时，⊙O是否可能与以C为圆心，BC长为半径的⊙C相切？如果可能，请求出两圆相切时的值；如果不可能，请说明理由．‎ 青浦区2010年初三学业考试模拟考 数学试卷答案　　 Q.2010.4‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．（B）；2．（C）；3．（D）；4．（C）；5．（B）；6．（B）．‎ 二、填空题：（本大题共12题，每题4分，满分48分） ‎ ‎7．；8．；9．；10．；11．；12．且；‎ ‎13．二；14．；15．；16．；17．；18．或．‎ 三、解答题：（本大题共7题，满分48分，第19-22题每题10分，第23-24题每题12分，第25题14分）‎ ‎19．解：原式 ……………………………………（4分）‎ ‎ ……………………………………………………………（2分）‎ ‎ …………………………………………………………………（1分）‎ 当 时，原式 ……………………………………………………（1分）‎ ‎ ………………………………………（1分）‎ ‎ …………………………………………………（1分）‎ ‎20． 解：由 ① 得 ③ ………………………………………………………（1分）‎ 把③代入② 得 ………………………………………………（1分） ‎ 即 …………………………………………………………………………（2分）‎ 解得 ， ……………………………………………………………………（2分）‎ 将代入③得 ………………………………………………………………（1分）‎ 将代入③得 …………………………………………………………………（1分）‎ 所以，原方程组的解为 ， …………………………………………（2分）‎ ‎21．解： ‎ ‎（1）a= 8 ，b= 0.24 ； ………………………………………………………………（4分）‎ ‎（2）补全频率分布直方图（略）；……………………………………………………………（2分）‎ ‎（3）样本中位数落在 80.5—90.5 （或第四）组内；……………………………………（2分）‎ ‎（4）该校参加这次竞赛成绩优秀的约有 216 人．…………………………………………（2分）‎ ‎22．证明：（1）由矩形ABCD，得∠B =∠C=，CD=AB，AD=BC，AD∥BC …（1分）‎ 由△DEC沿线段DE翻折，点C恰好落在线段AE上的点F处，得△DFE≌△DCE …（1分）‎ ‎∴DF = DC，∠DFE =∠C= ∴DF = AB，∠AFD= ∴∠AFD=∠B，…………（2分）‎ 由AD∥BC得∠DAF=∠AEB， ………………………………………………………… （1分）‎ ‎∴△ABE≌△DFA. …………………………………………………………………………（1分）‎ ‎（2）由ECBE=14，设CE=，BE=，则AD=BC= ‎ 由△ABE≌△DFA.得AF=BE= ………………………………………………………… （1分）‎ Rt△ADF中，由勾股定理可得DF= ……………………………………………………（1分）‎ 又DF=CD=AB=6∴ …………………………………………………………………（1分）‎ 在Rt△DCE中，DE= ………………………………（1分）‎ ‎23．解:（1）过E作EG⊥BC，垂足为G，由AB=4，E为AB的中点，得BE=2 ……（1分）‎ Rt△EBG中， ， ……………… （2分）‎ ‎（2）不变 ………………………………………………………………………………… （1分）‎ 解法（一）：在梯形ABCD中，由AD∥BC，MN∥AB，得MN=AB=4 ………………（1分）‎ 过点P作PH⊥MN，垂足为H ……………………………………………………………（1分）‎ 由MN∥AB得NMC=B= 所以PMH= ……………………………… （1分）‎ 由E、F是AB、DC边的中点 得EF∥BC，由EG⊥BC，PM⊥BC，得EG∥PM ‎∴PM = EG= ……………………………………………………………………………（1分）‎ 在Rt△PMH中，，所以PH=PM …………………（2分）‎ ‎∴ …………………………………………… （2分）‎ 解法（二）：延长MP交AD于点H，只要求出NH的长即可，评分标准可参考解法一.‎ ‎24．解：（1）由直线OA与反比例函数的图像交于点A(3，3)，得直线OA为：，‎ 双曲线为：，点B(6，m)代入 得 ，点B(6，) ， ……………（1分）‎ 设直线BC的解析式为 ，由直线BC经过点B，‎ 将，代入得 …………………………………………… （1分）‎ 所以，直线BC的解析式为 ………………………………………………… （1分）‎ ‎(1)由直线得点C(0，)，‎ 设经过A、B、C三点的二次函数的解析式为 将A、B两点的坐标代入，得 ………………… （1分）‎ 解得 ……………………………………………………………………………（1分）‎ 所以，抛物线的解析式为 ……………………………………………（1分）‎ ‎（3）存在 把配方得， ‎ 所以得点D(4，)，对称轴为直线 ………………………………………………（1分）‎ 得对称轴与轴交点的坐标为E(4，0). ………………………………………………（1分）‎ 由BD=，BC=，CD=,得，所以，∠DBC= ……（1分）‎ 又∠PEO=，若以O、E、P为顶点的三角形与△BCD相似，则有：‎ ‎①即 得，有(4，) ，(4，) ‎ ‎②即得， 有(4，12) ，(4，). …………（3分）‎ 所以，点P的坐标为 (4，) ， (4，)， (4，12) ， (4，).‎ ‎25． 解：（1）过点A作AEBC，垂足为E，由AB=AC，得BE=BC=2.…………（1分）‎ 在Rt△AEB中，∠AEB=，AE= …………………………………（1分）‎ ‎∴.………………………………………………………… （1分）‎ ‎（2）过点O作OFAD，垂足为F，则AF=DF= ………………………（1分）‎ BF=. ……………………………………………………………（1分）‎ ‎∵∠OFB=∠AEB=，∠OBF=∠ABE，∴△OBF∽△ABE …………………………（1分）‎ ‎∴，即 ……………………………………………………… （1分）‎ 整理得（）……………………………………………… （2分）‎ ‎(1)可能相切 在Rt△AEO中，∠AEO=，AE=1，OE=， ‎ 则AO= …………………………………………………（1分）‎ 设⊙C与BC边相交于点P，则⊙C的半径CP=BC=1，‎ ‎①若⊙O与⊙C外切，则有OA+CP=OC.‎ 即 解得 ………………………………………………………………………… （1分）‎ ‎②若⊙O与⊙C内切，则有.‎ ‎∵1OA ，PC=1，OA，∴只有.………………………… （1分）‎ 即 解得（不合题意，舍去）………………………………………………………… （1分）‎ 所以，当⊙O与⊙C相切时，. …………………………………………………… （1分）‎