中考数学二模试卷含解析21

中考数学二模试卷含解析21

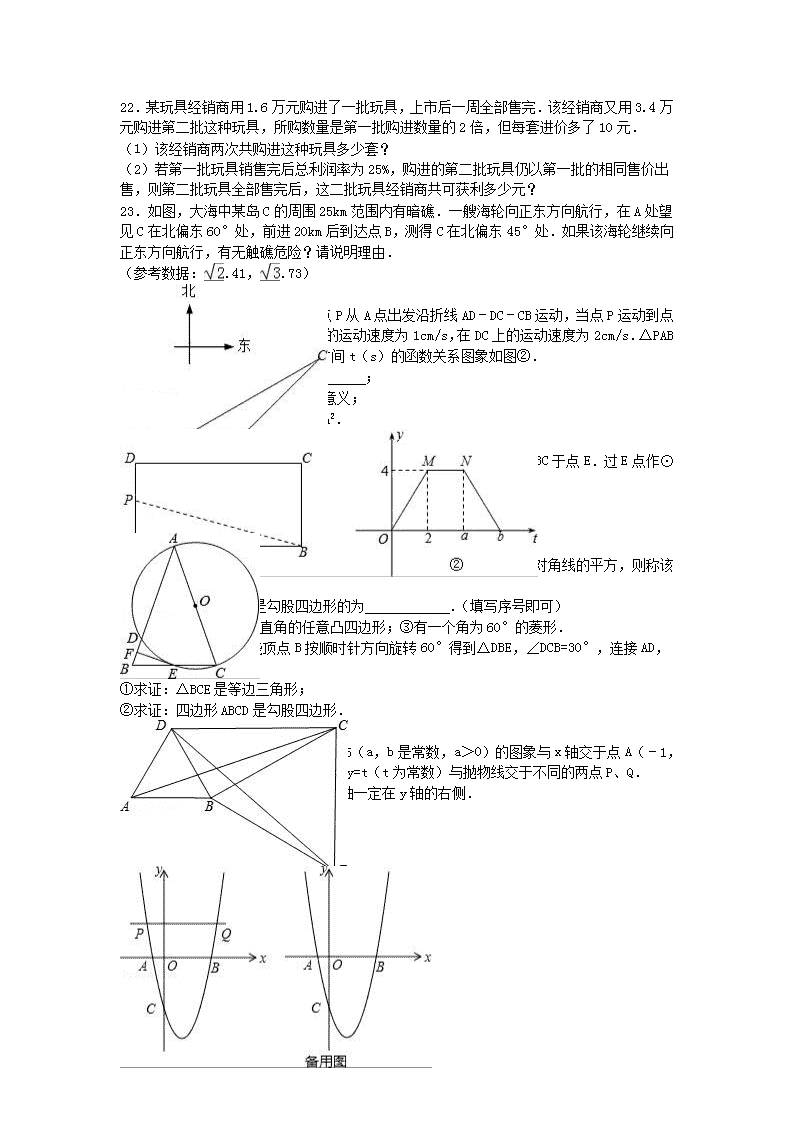
‎2016年江苏省南京市高淳区中考数学二模试卷 一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）‎ ‎1．在实数，0，﹣，2π中，无理数的个数有（　　）‎ A．0个 B．1个 C．2个 D．3个 ‎2．下列各式计算正确的是（　　）‎ A．a6÷a3=a2 B．（a3）2=a5 C． =±2 D． =﹣2‎ ‎3．某课外兴趣小组为了解所在地区的老年人的健康状况，分别作了四种不同的抽样调查，你认为抽样较合理的是（　　）‎ A．在公园调查了1000名老年人的健康状况 B．在医院调查了1000名老年人的健康状况 C．调查了100名小区内老年邻居的健康状况 D．利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 ‎4．如图是由3个相同的正方体组成的一个立体图形，它的三视图是（　　）‎ A． B． C． D．‎ ‎5．某种衬衫的价格经过连续两次的降价后，由每件150元降到96元，则平均每次降价的百分率是（　　）‎ A．10% B．15% C．20% D．30%‎ ‎6．如图，AB是半圆O直径，半径OC⊥AB，连接AC，∠CAB的平分线AD分别交OC于点E，交于点D，连接CD、OD，以下三个结论：①AC∥OD；②AC=2CD；③线段CD是CE与CO的比例中项，其中所有正确结论的序号是（　　）‎ A．①② B．①③ C．②③ D．①②③‎ ‎　‎ 二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题纸相应位置上）‎ ‎7．PM2.5是指大气中直径小于或等于2.5um（0.0000025m）的颗粒物，含有大量有毒、有害物质，也称可吸入肺颗粒物，将0.0000025用科学记数法表示为　　　　　　．‎ ‎8．不等式组的解集是　　　　　　．‎ ‎9．小明第一次抛一枚质地均匀的硬币时反面向上，第二次抛此枚硬币时也是反面向上，则他第三次抛这枚硬币时，正面向上的概率是　　　　　　．‎ ‎10．函数y=中，自变量x的取值范围是　　　　　　．‎ ‎11．我市某一周的最高气温统计如表，则这组数据的中位数是　　　　　　．‎ 最高气温（℃）‎ ‎25‎ ‎26‎ ‎27‎ ‎28‎ 天 数 ‎1‎ ‎2‎ ‎1‎ ‎3‎ ‎12．如图，在四边形ABCD中，AD∥BC，对角线AC、BD交于点O，S△AOD：S△BOC=1：9，AD=2，则BC的长是　　　　　　．‎ ‎13．如图，MN是⊙O的直径，矩形ABCD的顶点A、D在MN上，顶点B、C在⊙O上，若⊙O的半径为5，AB=4，则AD边的长为　　　　　　．‎ ‎14．将面积为32π的半圆围成一个圆锥的侧面，则这个圆锥的底面半径为　　　　　　．‎ ‎15．如图，点P在函数y=（x＞0）的图象上运动，O为坐标原点，点A为PO的中点，以点P为圆心，PA为半径作⊙P，则当⊙P与坐标轴相切时，点P的坐标为　　　　　　．‎ ‎16．矩形ABCD中，AB=10，BC=4，Q为AB边的中点，P为CD边上的动点，且△AQP是腰长为5的等腰三角形，则CP的长为　　　　　　．‎ ‎　‎ 三、解答题（本大题共11小题，共88分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）‎ ‎17．计算：‎ ‎（1）2cos45°+（2﹣π）0﹣（）﹣2；‎ ‎（2）（﹣）÷．‎ ‎18．已知关于x的一元二次方程x2﹣ax+2=0的两实数根x1、x2满足x1x2=x1+x2﹣2．‎ ‎（1）求a的值；‎ ‎（2）求出该一元二次方程的两实数根．‎ ‎19．为了增强环境保护意识，在“世界环境日”当天，在环保局工作人员指导下，若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组，随机抽查了全市40个噪声测量点在某时刻的噪声声级（单位：dB），并将抽查得到的数据进行整理（设所测数据是正整数），得频数分布表如表：‎ 组 别 噪声声级分组 频 数 频 率 ‎1‎ ‎44.5﹣59.5‎ ‎4‎ ‎0.1‎ ‎2‎ ‎59.5﹣74.5‎ a ‎0.2‎ ‎3‎ ‎74.5﹣89.5‎ ‎10‎ ‎0.25‎ ‎4‎ ‎89.5﹣104.5‎ b c ‎5‎ ‎104.5﹣119.5‎ ‎6‎ ‎0.15‎ 合 计 ‎40‎ ‎1.00‎ 根据表中提供的信息解答下列问题：‎ ‎（1）频数分布表中的a=　　　　　　，b=　　　　　　，c=　　　　　　；‎ ‎（2）补充完整频数分布直方图；‎ ‎（3）如果全市共有400个测量点，那么在这一时刻噪声声级小于75dB的测量点约有多少个？‎ ‎20．（1）甲、乙两人用如图所示的①、②两个转盘做游戏，规则是：转动两个转盘各1次，若两个转盘停止转动后，指针所在区域的两个数字之积为奇数，则甲获胜，否则乙胜．试求出甲获胜的概率．‎ ‎（2）若利用除颜色外其余都相同的红、黄、白色乒乓球各一个设计一个摸球试验，试写出一个与（1）中甲获胜概率相同的事件．（友情提醒：要说明试验的方案，不需说明理由）‎ ‎21．如图，D是线段AB的中点，C是线段AB的垂直平分线上的一点，DE⊥AC于点E，DF⊥BC于点F．‎ ‎（1）求证：DE=DF；‎ ‎（2）当CD与AB满足怎样的数量关系时，四边形CEDF为正方形？请说明理由．‎ ‎22．某玩具经销商用1.6万元购进了一批玩具，上市后一周全部售完．该经销商又用3.4万元购进第二批这种玩具，所购数量是第一批购进数量的2倍，但每套进价多了10元．‎ ‎（1）该经销商两次共购进这种玩具多少套？‎ ‎（2）若第一批玩具销售完后总利润率为25%，购进的第二批玩具仍以第一批的相同售价出售，则第二批玩具全部售完后，这二批玩具经销商共可获利多少元？‎ ‎23．如图，大海中某岛C的周围25km范围内有暗礁．一艘海轮向正东方向航行，在A处望见C在北偏东60°处，前进20km后到达点B，测得C在北偏东45°处．如果该海轮继续向正东方向航行，有无触礁危险？请说明理由．‎ ‎（参考数据：≈1.41，≈1.73）‎ ‎24．如图①，在矩形ABCD中，动点P从A点出发沿折线AD﹣DC﹣CB运动，当点P运动到点B时停止．已知动点P在AD、BC上的运动速度为1cm/s，在DC上的运动速度为2cm/s．△PAB的面积y（cm2）与动点P的运动时间t（s）的函数关系图象如图②．‎ ‎（1）a=　　　　　　，b=　　　　　　；‎ ‎（2）用文字说明点N坐标的实际意义；‎ ‎（3）当t为何值时，y的值为2cm2．‎ ‎25．如图，在△ABC中，AB=AC．以AC为直径的⊙O交AB于点D，交BC于点E．过E点作⊙O的切线，交AB于点F．‎ ‎（1）求证：EF⊥AB；‎ ‎（2）若BD=2，BE=3，求AC的长．‎ ‎26．给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．‎ ‎（1）以下四边形中，是勾股四边形的为　　　　　　．（填写序号即可）‎ ‎①矩形；②有一个角为直角的任意凸四边形；③有一个角为60°的菱形．‎ ‎（2）如图，将△ABC绕顶点B按顺时针方向旋转60°得到△DBE，∠DCB=30°，连接AD，DC，CE．‎ ‎①求证：△BCE是等边三角形；‎ ‎②求证：四边形ABCD是勾股四边形．‎ ‎27．如图，已知二次函数y=ax2+bx﹣5（a，b是常数，a＞0）的图象与x轴交于点A（﹣1，0）和点B，与y轴交于点C．动直线y=t（t为常数）与抛物线交于不同的两点P、Q．‎ ‎（1）若a＜5，试证明抛物线的对称轴一定在y轴的右侧．‎ ‎（2）若点B的坐标为（5，0）．‎ ‎①求a、b的值及t的取值范围．‎ ‎②求当t为何值时，∠PCQ=90°．‎ ‎　‎ ‎2016年江苏省南京市高淳区中考数学二模试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）‎ ‎1．在实数，0，﹣，2π中，无理数的个数有（　　）‎ A．0个 B．1个 C．2个 D．3个 ‎【考点】无理数．‎ ‎【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．‎ ‎【解答】解：，0是有理数；‎ ‎﹣、2π是无理数，‎ 故选：C．‎ ‎　‎ ‎2．下列各式计算正确的是（　　）‎ A．a6÷a3=a2 B．（a3）2=a5 C． =±2 D． =﹣2‎ ‎【考点】同底数幂的除法；算术平方根；立方根；幂的乘方与积的乘方．‎ ‎【分析】根据同底数幂的除法底数不变指数相减；幂的乘方底数不变指数相乘；一个正数的算术平方根只有一个；负数的立方根是负数，可得答案．‎ ‎【解答】解：A、同底数幂的除法底数不变指数相减，故A错误；‎ B、幂的乘方底数不变指数相乘，故B错误；‎ C、=2，故C错误；‎ D、=﹣2，故D正确；‎ 故选：D．‎ ‎　‎ ‎3．某课外兴趣小组为了解所在地区的老年人的健康状况，分别作了四种不同的抽样调查，你认为抽样较合理的是（　　）‎ A．在公园调查了1000名老年人的健康状况 B．在医院调查了1000名老年人的健康状况 C．调查了100名小区内老年邻居的健康状况 D．利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 ‎【考点】抽样调查的可靠性．‎ ‎【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性，所谓代表性，就是抽取的样本必须是随机的，即各个方面，各个层次的对象都要有所体现．‎ ‎【解答】解：A、在公园调查了1000名老年人的健康状况，抽查的都是锻炼的老人，没有代表性，故A错误；‎ B、在医院调查了1000名老年人的健康状况，抽查的都是不健康的老人，没有代表性，故B错误；‎ C、调查了100名小区内老年邻居的健康状况，调查没有广泛性，故C错误；‎ D、利用派出所的户籍网随机调查了该地区10%的老年人的健康状况，调查由广泛性、代表性，故D正确；‎ 故选：D．‎ ‎　‎ ‎4．如图是由3个相同的正方体组成的一个立体图形，它的三视图是（　　）‎ A． B． C． D．‎ ‎【考点】简单组合体的三视图．‎ ‎【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．‎ ‎【解答】解：所给图形的三视图是A选项所给的三个图形．‎ 故选：A．‎ ‎　‎ ‎5．某种衬衫的价格经过连续两次的降价后，由每件150元降到96元，则平均每次降价的百分率是（　　）‎ A．10% B．15% C．20% D．30%‎ ‎【考点】一元二次方程的应用．‎ ‎【分析】如果价格每次降价的百分率为x，降一次后就是降到价格的（1﹣x）倍，连降两次就是降到原来的（1﹣x）2倍．则两次降价后的价格是150×（1﹣x）2，即可列方程求解．‎ ‎【解答】解：设平均每次降价的百分率为x，‎ 则可以得到关系式：150×（1﹣x）2=96，‎ 解得x=0.2或1.8，‎ x=1.8不符合题意，舍去，‎ 故x=0.2．‎ 答：平均每次降价的百分率是20%．‎ 故选C．‎ ‎　‎ ‎6．如图，AB是半圆O直径，半径OC⊥AB，连接AC，∠CAB的平分线AD分别交OC于点E，交于点D，连接CD、OD，以下三个结论：①AC∥OD；②AC=2CD；③线段CD是CE与CO的比例中项，其中所有正确结论的序号是（　　）‎ A．①② B．①③ C．②③ D．①②③‎ ‎【考点】圆周角定理；圆心角、弧、弦的关系；相似三角形的判定与性质．‎ ‎【分析】由OA=OD，利用等边对等角得到一对角相等，再由AD为角平分线得到一对角相等，等量代换得到一对内错角相等，利用内错角相等两直线平行即可得到AC与OD平行，故选项①正确；由CO垂直于AB，OA=OC，得到三角形AOC为等腰直角三角形，得到∠CAB为45度，再由两直线平行同位角相等得到∠DOB为45度，即∠COD为45度，再由同弧所对的圆周角等于圆心角的一半得到∠ADC为45度，得到一对角相等，再由一对公共角，利用两对对应角相等的两三角形相似得到三角形CED与三角形OCD相似，由相似得比例可得出CD为CE与CO的比例中项，故选项③正确；取弧AC的中点F，得到弧AF与弧CF相等，再由弧AC=2弧CD，得到三条弧相等，利用等弧对等弦得到CF=AF=CD，即CF+AF=2CD，而CF+AF大于AC，可得出AC不等式2CD，故选项②错误．‎ ‎【解答】解：∵OA=OD，‎ ‎∴∠OAD=∠ODA，‎ ‎∵AD为∠CAB的平分线，‎ ‎∴∠CAD=∠OAD，‎ ‎∴∠CAD=∠ODA，‎ ‎∴AC∥OD，故选项①正确；‎ ‎∵OC⊥AB，OA=OC，‎ ‎∴△AOC为等腰直角三角形，‎ ‎∴∠DOB=∠COD=∠BAC=45°，‎ ‎∵∠ADC与∠AOC都对，‎ ‎∴∠ADC=∠AOC=45°，‎ ‎∴∠ADC=∠COD，又∠OCD=∠DCE，‎ ‎∴△DCE∽△OCD，‎ ‎∴=，即CD2=CE•OC，‎ 故选项③正确；‎ 取的中点F，可得=，‎ ‎∵=2，‎ ‎∴==，‎ ‎∴AF=FC=CD，即AF+FC=2CD，‎ ‎∵AF+FC＞AC，‎ 则2CD＞AC，故选项②错误，‎ 则正确的选项有：①③．‎ 故选B ‎　‎ 二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题纸相应位置上）‎ ‎7．PM2.5是指大气中直径小于或等于2.5um（0.0000025m）的颗粒物，含有大量有毒、有害物质，也称可吸入肺颗粒物，将0.0000025用科学记数法表示为　2.5×10﹣6　．‎ ‎【考点】科学记数法—表示较小的数．‎ ‎【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．‎ ‎【解答】解：0.000 0025=2.5×10﹣6；‎ 故答案为2.5×10﹣6．‎ ‎　‎ ‎8．不等式组的解集是　x＞3　．‎ ‎【考点】解一元一次不等式组．‎ ‎【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．‎ ‎【解答】解：解不等式﹣2x＜6，得：x＞﹣3，‎ 解不等式﹣2+x＞1，得：x＞3，‎ 故不等式组的解集为：x＞3，‎ 故答案为：x＞3．‎ ‎　‎ ‎9．小明第一次抛一枚质地均匀的硬币时反面向上，第二次抛此枚硬币时也是反面向上，则他第三次抛这枚硬币时，正面向上的概率是　　．‎ ‎【考点】概率公式．‎ ‎【分析】根据一枚质地均匀的硬币有正反两面即可得出结论．‎ ‎【解答】解：∵一枚质地均匀的硬币有正反两面，‎ ‎∴他第三次抛这枚硬币时，正面向上的概率是．‎ 故答案为：．‎ ‎　‎ ‎10．函数y=中，自变量x的取值范围是　x≤3　．‎ ‎【考点】函数自变量的取值范围．‎ ‎【分析】根据被开方数大于等于0列式计算即可得解．‎ ‎【解答】解：由题意得，3﹣x≥0，‎ 解得x≤3．‎ 故答案为：x≤3．‎ ‎　‎ ‎11．我市某一周的最高气温统计如表，则这组数据的中位数是　27℃　．‎ 最高气温（℃）‎ ‎25‎ ‎26‎ ‎27‎ ‎28‎ 天 数 ‎1‎ ‎2‎ ‎1‎ ‎3‎ ‎【考点】中位数．‎ ‎【分析】找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数．‎ ‎【解答】解：处于这组数据中间位置的那个数是27℃，由中位数的定义可知，这组数据的中位数是27℃．‎ 故答案为27℃．‎ ‎　‎ ‎12．如图，在四边形ABCD中，AD∥BC，对角线AC、BD交于点O，S△AOD：S△BOC=1：9，AD=2，则BC的长是　6　．‎ ‎【考点】相似三角形的判定与性质．‎ ‎【分析】根据S△AOD：S△BOC=1：9，利用△AOD～△COB，则得出AD：BC=1：3，即可求出BC的长．‎ ‎【解答】解：∵AD∥BC，‎ ‎∴△AOD～△COB，‎ ‎∵S△AOD：S△BOC=1：9，‎ ‎∴AD：BC=1：3，‎ ‎∵AD=2，‎ ‎∴BC=6．‎ 故答案为：6．‎ ‎　‎ ‎13．如图，MN是⊙O的直径，矩形ABCD的顶点A、D在MN上，顶点B、C在⊙O上，若⊙O的半径为5，AB=4，则AD边的长为　6　．‎ ‎【考点】垂径定理；勾股定理；矩形的性质．‎ ‎【分析】连接OB，根据矩形性质得出AB=CD=4，∠BAO=∠CDO=90°，根据勾股定理求出AO、DO，即可得出答案．‎ ‎【解答】解：‎ 连接OB，‎ ‎∵四边形ABCD是矩形，‎ ‎∴AB=CD=4，∠BAO=∠CDO=90°，‎ ‎∵OB=5，‎ ‎∴AO==3，‎ 同理DO=3，‎ ‎∴AD=3+3=6，‎ 故答案为：6．‎ ‎　‎ ‎14．将面积为32π的半圆围成一个圆锥的侧面，则这个圆锥的底面半径为　4　．‎ ‎【考点】圆锥的计算．‎ ‎【分析】由半圆的面积求出半圆的半径，而半圆的半径等于圆锥的母线l，利用圆锥的面积公式求出圆锥的半径即可．‎ ‎【解答】解：设半圆的半径为R，‎ ‎∵S=πR2=32π，‎ 解得：R=8，即l=8，‎ ‎∵S侧=S=πrl=8πr=32π，‎ 则r=4．‎ 故答案为：4．‎ ‎　‎ ‎15．如图，点P在函数y=（x＞0）的图象上运动，O为坐标原点，点A为PO的中点，以点P为圆心，PA为半径作⊙P，则当⊙P与坐标轴相切时，点P的坐标为　（，1）或（1，）　．‎ ‎【考点】反比例函数图象上点的坐标特征；切线的性质．‎ ‎【分析】结合点P在反比例函数图象上，设出点P的坐标，由两点间的距离公式求出OP的长度，由点A为OP的中点，即可找出PA的长度，再根据相切的两种不同形式分类，结合点P的坐标以及圆的半径即可得出关于P点横坐标的一元高次方程，解方程即可得出结论．‎ ‎【解答】解：∵点P为函数y=（x＞0）的图象上的点，‎ ‎∴设点P的坐标为（n，）（n＞0）．‎ ‎∴OP=．‎ ‎∵点A为PO的中点，‎ ‎∴PA=OP=．‎ ‎⊙P与坐标轴相切分两种情况：‎ ‎①⊙P与x轴相切，此时有=，‎ 整理得：n2=，解得：n2=3，或n2=﹣3（舍去），‎ 解n2=3，得：n1=，n2=﹣（舍去），‎ 此时点P的坐标为（，1）；‎ ‎②⊙P与y轴相切，此时有=n，‎ 整理得：n2=，解得：n2=1，或n2=﹣1（舍去），‎ 解n2=1，得：n3=1，a4=﹣1（舍去），‎ 此时点P的坐标为（1，）．‎ 综上可知：点P的坐标为（，1）或（1，）．‎ 故答案为：（，1）或（1，）．‎ ‎　‎ ‎16．矩形ABCD中，AB=10，BC=4，Q为AB边的中点，P为CD边上的动点，且△AQP是腰长为5的等腰三角形，则CP的长为　2、7或8　．‎ ‎【考点】矩形的性质；等腰三角形的性质．‎ ‎【分析】首先计算出QB的长，再分三种情况：①如图1，PQ=AQ=5时；②如图2，AP=AQ=5时；③如图3，PQ=AQ=5且△PBQ为钝角三角形时分别计算出CP的长即可．‎ ‎【解答】解：∵AB=10，点Q是BA的中点，‎ ‎∴AQ=BA=×10=5，‎ ‎∵四边形ABCD是矩形，‎ ‎∴DC=AB=10，∠B=∠C=∠D=90°，‎ ‎①如图1，PQ=AQ=5时，过点P作PE⊥BA于E，‎ 根据勾股定理，QE==3，‎ ‎∴BE=BQ+QE=5+3=8，‎ ‎∴CP=BE=8；‎ ‎②如图2，AP=AQ=5时，‎ 根据勾股定理，DP===3，‎ ‎∴CP=10﹣3=7；‎ ‎③如图3，PQ=AQ=5且△PBQ为钝角三角形时，过点P作PE⊥BA于E，‎ 根据勾股定理：QE===3，‎ ‎∵BE=QB﹣EQ=5﹣3=2，‎ ‎∴CP=BE=2，‎ 综上所述，CP的长为2或7或8．‎ 故答案为：2、7或8．‎ ‎　‎ 三、解答题（本大题共11小题，共88分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）‎ ‎17．计算：‎ ‎（1）2cos45°+（2﹣π）0﹣（）﹣2；‎ ‎（2）（﹣）÷．‎ ‎【考点】实数的运算；分式的混合运算；零指数幂；负整数指数幂；特殊角的三角函数值．‎ ‎【分析】（1）原式利用零指数幂、负整数指数幂法则，以及特殊角的三角函数值计算即可得到结果；‎ ‎（2）原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．‎ ‎【解答】解：（1）原式=2×+1﹣9=﹣8；‎ ‎（2）原式=（﹣）÷=×=．‎ ‎　‎ ‎18．已知关于x的一元二次方程x2﹣ax+2=0的两实数根x1、x2满足x1x2=x1+x2﹣2．‎ ‎（1）求a的值；‎ ‎（2）求出该一元二次方程的两实数根．‎ ‎【考点】根与系数的关系．‎ ‎【分析】（1）根据根与系数的关系的关系x1+x2=a，x1x2=2，如何根据x1x2=x1+x2﹣2得到关于a的方程，解方程即可得到结论；‎ ‎（2）解方程即可得到结果．‎ ‎【解答】解：（1）∵x1+x2=a，x1x2=2，‎ 又x1x2=x1+x2﹣2，‎ ‎∴a﹣2=2，a=4；‎ ‎（2）方程可化为x2﹣4x+2=0，‎ ‎∴（x﹣2）2=2，‎ 解得：x﹣2= 或x﹣2=﹣，‎ ‎∴x1=2+，x2=2﹣．‎ ‎　‎ ‎19．为了增强环境保护意识，在“世界环境日”当天，在环保局工作人员指导下，若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组，随机抽查了全市40个噪声测量点在某时刻的噪声声级（单位：dB），并将抽查得到的数据进行整理（设所测数据是正整数），得频数分布表如表：‎ 组 别 噪声声级分组 频 数 频 率 ‎1‎ ‎44.5﹣59.5‎ ‎4‎ ‎0.1‎ ‎2‎ ‎59.5﹣74.5‎ a ‎0.2‎ ‎3‎ ‎74.5﹣89.5‎ ‎10‎ ‎0.25‎ ‎4‎ ‎89.5﹣104.5‎ b c ‎5‎ ‎104.5﹣119.5‎ ‎6‎ ‎0.15‎ 合 计 ‎40‎ ‎1.00‎ 根据表中提供的信息解答下列问题：‎ ‎（1）频数分布表中的a=　8　，b=　12　，c=　0.3　；‎ ‎（2）补充完整频数分布直方图；‎ ‎（3）如果全市共有400个测量点，那么在这一时刻噪声声级小于75dB的测量点约有多少个？‎ ‎【考点】频数（率）分布直方图；用样本估计总体；频数（率）分布表．‎ ‎【分析】（1）根据表格可以得到a、b、c的值；‎ ‎（2）根据表格中的数据可以将频数分布直方图补充完整；‎ ‎（3）根据题意可以得到全市共有400个测量点，在这一时刻噪声声级小于75dB的测量点约有多少个．‎ ‎【解答】解：（1）由题意可得，‎ a=40×0.2=8，b=40﹣4﹣8﹣10﹣6=12，c=12÷40=0.3，‎ 故答案为：8，12，0.3；‎ ‎（2）补充完整频数分布直方图如下图所示，‎ ‎（3）由题意可得，‎ ‎400×（0.1+0.2）=400×0.3=120（个）‎ 即在这一时刻噪声声级小于75dB的测量点约有120个．‎ ‎　‎ ‎20．（1）甲、乙两人用如图所示的①、②两个转盘做游戏，规则是：转动两个转盘各1次，若两个转盘停止转动后，指针所在区域的两个数字之积为奇数，则甲获胜，否则乙胜．试求出甲获胜的概率．‎ ‎（2）若利用除颜色外其余都相同的红、黄、白色乒乓球各一个设计一个摸球试验，试写出一个与（1）中甲获胜概率相同的事件．（友情提醒：要说明试验的方案，不需说明理由）‎ ‎【考点】列表法与树状图法．‎ ‎【分析】（1）列举得出所有等可能的情况数，找出积为奇数的情况数，即可求出甲获胜的概率；‎ ‎（2）求出甲乙两人获胜的概率，比较即可得到游戏不公平，修改规则即可．‎ ‎【解答】解：‎ ‎ （1）转动两个转盘各1次，所有可能出现的结果有（1，5）、（1，6）、（1，7）、‎ ‎（2，5）、（2，6）、（2，7）、（3，5）、（3，6）、（3，7），共有9种可能．‎ 它们出现的可能性相同，所有结果中，满足“积为奇数”的结果有4种，‎ 所以转动两个转盘各1次，转出的两个数字之积为奇数的概率为．‎ ‎（2）实验如：在一个不透明的袋子中放入除颜色外其余都相同的红、黄、白色乒乓球各1个，从袋子中取出一个球，记下颜色后放入袋中，再从袋子中取出一个球，记下颜色．事件：两次取出的球中有且只有一个球是红色球．‎ ‎　‎ ‎21．如图，D是线段AB的中点，C是线段AB的垂直平分线上的一点，DE⊥AC于点E，DF⊥BC于点F．‎ ‎（1）求证：DE=DF；‎ ‎（2）当CD与AB满足怎样的数量关系时，四边形CEDF为正方形？请说明理由．‎ ‎【考点】正方形的判定；全等三角形的判定与性质．‎ ‎【分析】（1）由CD垂直平分线AB，可得AC=CB，得出∠ACD=∠BCD，再由∠EDC=∠FDC=90°，可证得△ACD≌△BCD，得出CE=CF即可；‎ ‎（2）先证明四边形CEDF是矩形，再证出因此AB=2CD时，四边形CEDF为正方形．‎ ‎【解答】（1）证明：∵CD垂直平分线AB，‎ ‎∴AC=CB．‎ ‎∴△ABC是等腰三角形，‎ ‎∵CD⊥AB，‎ ‎∴∠ACD=∠BCD．‎ ‎∵DE⊥AC，DF⊥BC，‎ ‎∴∠DEC=∠DFC=90°‎ ‎∴∠EDC=∠FDC，‎ 在△DEC与△DFC中，，‎ ‎∴△DEC≌△DFC（ASA），‎ ‎∴DE=DF；‎ ‎（2）解：当AB=2CD时，四边形CEDF为正方形．理由如下：‎ ‎∵AD=BD，AB=2CD，‎ ‎∴AD=BD=CD．‎ ‎∴∠ACD=45°，∠DCB=45°，‎ ‎∴∠ACB=∠ACD+∠BCD=90°，‎ ‎∴四边形DECF是矩形．‎ 又∵DE=DF，‎ ‎∴四边形CEDF是正方形．‎ ‎　‎ ‎22．某玩具经销商用1.6万元购进了一批玩具，上市后一周全部售完．该经销商又用3.4万元购进第二批这种玩具，所购数量是第一批购进数量的2倍，但每套进价多了10元．‎ ‎（1）该经销商两次共购进这种玩具多少套？‎ ‎（2）若第一批玩具销售完后总利润率为25%，购进的第二批玩具仍以第一批的相同售价出售，则第二批玩具全部售完后，这二批玩具经销商共可获利多少元？‎ ‎【考点】分式方程的应用．‎ ‎【分析】（1）设第一次购进了x套，则第二次购进了2x套，进而表示出进价，即可得出等式求出答案；‎ ‎（2）首先求出玩具的售价，进而求出其每件的利润，即可得出答案．‎ ‎【解答】解：（1）设第一次购进了x套，则第二次购进了2x套．‎ 依题意，列方程得： +10=，‎ 解得：x=100，‎ 经检验x=100是原方程的根，2x=200，‎ 答：该经销商两次共购进这种玩具300套；‎ ‎（2）由（1）得第一批每套玩具的进价为=160（元），‎ 又∵总利润率为25%，‎ ‎∴售价为160（1+25%）=200元，‎ 第二批玩具的进价为170元，售价也为200元．‎ ‎40×100+30×200=10000元．‎ 答：这二批玩具经销商共可获利10000元．‎ ‎　‎ ‎23．如图，大海中某岛C的周围25km范围内有暗礁．一艘海轮向正东方向航行，在A处望见C在北偏东60°处，前进20km后到达点B，测得C在北偏东45°处．如果该海轮继续向正东方向航行，有无触礁危险？请说明理由．‎ ‎（参考数据：≈1.41，≈1.73）‎ ‎【考点】解直角三角形的应用-方向角问题．‎ ‎【分析】判断有无危险只要求出点C到AB的距离，与6海里比较大小就可以．首先过点C作CD⊥AB于点D，设BD=xkm，由三角函数的定义，即可求得CD=xkm，AD=xkm，则可方程20+x=x，解此方程即可求得CD的长，比较即可求得答案．‎ ‎【解答】解：该海轮继续向正东方向航行，无触礁危险．‎ 理由：过点C作CD⊥AB于点D，‎ ‎∴∠BCD=∠CBM=45°，‎ 设BD=xkm，则CD==x（km），‎ ‎∵∠CAN=60°，‎ ‎∴∠CAD=30°，‎ 在Rt△CAD中，tan∠CAB=tan30°==，‎ ‎∴AD=CD=x（km），‎ ‎∵AB=20km，AB+DB=AD，‎ ‎∴20+x=x，‎ 解得：x=10+10（km），‎ ‎∴CD=10+10≈27.3（km）＞25km，‎ ‎∴该海轮继续向正东方向航行，无触礁危险．‎ ‎　‎ ‎24．如图①，在矩形ABCD中，动点P从A点出发沿折线AD﹣DC﹣CB运动，当点P运动到点B时停止．已知动点P在AD、BC上的运动速度为1cm/s，在DC上的运动速度为2cm/s．△PAB的面积y（cm2）与动点P的运动时间t（s）的函数关系图象如图②．‎ ‎（1）a=　4　，b=　6　；‎ ‎（2）用文字说明点N坐标的实际意义；‎ ‎（3）当t为何值时，y的值为2cm2．‎ ‎【考点】四边形综合题．‎ ‎【分析】（1）从图②中根据面积和运动时间求出AD，AB，从而得到a，b；‎ ‎（2）从图②中点N的纵坐标和横坐标分别考虑，结合图①即可；‎ ‎（3）y是2cm2的话，由于AB=4，只有点P到AB的距离为1，即可．‎ ‎【解答】解：（1）由图②中发现，点P从开始运动到2s时运动到点D，且在AD边上速度为1，‎ ‎∴BC=AD=2，‎ ‎∵点P在DC上运动时，面积不变是4，‎ ‎∴4=AB×AD，‎ ‎∴AB=4，‎ ‎∵DC上的运动速度为2cm/s，‎ ‎∴a=2+4÷2=4，‎ ‎∴b=2+2+2=6，‎ 故答案为4，6；‎ ‎（2）P运动了4s时到达点C，此时△PAB的面积为4cm2，‎ ‎（3）由题意AB=DC=4，‎ ‎∵要y的值为2cm2，即点P到AB的距离为1，‎ ‎∴必须点P在AD或BC上，且PA=1cm或PB=1cm，‎ 当PA=1cm时，点P的运动时间t=1s，‎ 当PB=1cm时，点P的运动时间为t=6﹣1=5s，‎ 即当t为1s或5s时，y的值为2cm2．‎ ‎　‎ ‎25．如图，在△ABC中，AB=AC．以AC为直径的⊙O交AB于点D，交BC于点E．过E点作⊙O的切线，交AB于点F．‎ ‎（1）求证：EF⊥AB；‎ ‎（2）若BD=2，BE=3，求AC的长．‎ ‎【考点】切线的性质．‎ ‎【分析】（1）连结OE．由AC=AC，OE=OC可证明∠OEC=∠ABC，从而可证得OE∥AB，由切线的性质可知∠OEF=90°，然后由平行线的性质可证明∠AFE=90°；‎ ‎（2）连结DE、AE．先由直径所对的圆周角等于90°可证明AE⊥BC，由等腰三角三线合一的性质可求得BC的长，然后依据圆内接四边形的性质证明∠BED=∠BAC，于是可得得到△BED∽△BAC，接下来由相似三角形对应边成比例可求得AB的长，从而得到AC的长．‎ ‎【解答】解：（1）证明：如图1所示：连结OE．‎ ‎∵AB=AC，‎ ‎∴∠B=∠ACB．‎ 又∵OE=OC，‎ ‎∴∠OEC=∠ACB，‎ ‎∴∠OEC=∠ABC．‎ ‎∴OE∥AB．‎ ‎∵EF与⊙O 相切，‎ ‎∴OE⊥EF．‎ ‎∴∠OEF=90°．‎ ‎∵OE∥AB，‎ ‎∴∠AFE=90°．‎ ‎∴OE⊥AB．‎ ‎（2）如图2所示：连结DE、AE．‎ ‎∵四边形ACED为⊙O的内接四边形，‎ ‎∴∠DEC+∠BAC=180°．‎ 又∵∠DEB+∠DEC=180°，‎ ‎∴∠BED=∠BAC．‎ 又∵∠B=∠B，‎ ‎∴△BED∽△BAC．‎ ‎∴．‎ ‎∵AC为⊙O的直径，‎ ‎∴∠AEC=90°．‎ ‎∵在△ABC中，AB=AC，‎ ‎∴BE=CE=3，‎ ‎∴BC=6．‎ ‎∴，‎ ‎∴AB=9．即AC=AB=9．‎ ‎　‎ ‎26．给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．‎ ‎（1）以下四边形中，是勾股四边形的为　①②　．（填写序号即可）‎ ‎①矩形；②有一个角为直角的任意凸四边形；③有一个角为60°的菱形．‎ ‎（2）如图，将△ABC绕顶点B按顺时针方向旋转60°得到△DBE，∠DCB=30°，连接AD，DC，CE．‎ ‎①求证：△BCE是等边三角形；‎ ‎②求证：四边形ABCD是勾股四边形．‎ ‎【考点】四边形综合题．‎ ‎【分析】（1）由勾股四边形的定义和特殊四边形的性质，则可得出；‎ ‎（2）①由旋转的性质可知△ABC≌△DBE，从而可得BC=BE，由∠CBE=60°可得△BCE为等边三角形；②由①可得∠BCE=60°，从而可知△DCE是直角三角形，再利用勾股定理即可解决问题．‎ ‎【解答】解：（1）①如图，‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠B=90°，‎ ‎∴AB2+BC2=AC2，‎ 即：矩形是勾股四边形，‎ ‎②如图，‎ ‎∵∠B=90°，‎ ‎∴AB2+BC2=AC2，‎ 即：由一个角为直角的四边形是勾股四边形，‎ ‎③有一个角为60°的菱形，邻边边中没有直角，所以不满足勾股四边形的定义，‎ 故答案为①②，‎ ‎（2）①∵△ABC绕点B顺时针旋转了60°到△DBE，‎ ‎∴BC=BE，∠CBE=60°，‎ ‎∵在△BCE中，BC=BE，∠CBE=60°‎ ‎∴△BCE是等边三角形．‎ ‎②∵△BCE是等边三角形，‎ ‎∴BC=CE，∠BCE=60°，‎ ‎∵∠DCB=30°，‎ ‎∴∠DCE=∠DCB+∠BCE=90°，‎ 在Rt△DCE中，有DC2+CE2=DE2，‎ ‎∵DE=AC，BC=CE，‎ ‎∴DC2+BC2=AC2，‎ ‎∴四边形ABCD是勾股四边形．‎ ‎　‎ ‎27．如图，已知二次函数y=ax2+bx﹣5（a，b是常数，a＞0）的图象与x轴交于点A（﹣1，0）和点B，与y轴交于点C．动直线y=t（t为常数）与抛物线交于不同的两点P、Q．‎ ‎（1）若a＜5，试证明抛物线的对称轴一定在y轴的右侧．‎ ‎（2）若点B的坐标为（5，0）．‎ ‎①求a、b的值及t的取值范围．‎ ‎②求当t为何值时，∠PCQ=90°．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）把A点坐标代入y=ax2+bx﹣5得到b=a﹣5，再利用抛物线的对称轴方程得到x=﹣=，然后根据0＜a＜5可判断＞0，所以此时抛物线的对称轴一定在y轴的右侧；‎ ‎（2）①把A和B点坐标代入y=ax2+bx﹣5中可得到关于a和b的方程组，然后解方程组可得到a和b的值，从而得到二次函数关系式为y=x2﹣4x﹣5，利用配方法求出抛物线的顶点坐标为（2，﹣9），再利用图象可判断当t＞﹣9时，动直线y=t（t为常数）与抛物线交于不同的两点；‎ ‎②直线y=t交y轴于点D，连接PC、CQ，如图，设点Q的坐标为（m，t）（m＞0），利用抛物线的对称性可得点P的坐标为（﹣m+4，t），分类讨论：（Ⅰ）当t＞﹣5时，点D在点C上方，把Q（m，t）代入解析式得到t+5=m2﹣4m，则CD=t+5，DQ=m，DP=m﹣4，再证明△QCD∽△CDP，利用相似比得到=，整理得（t+5）2=m2﹣4m，则（t+5）2=t+5，解得t1=﹣5（不合，舍去），t2=﹣4；（Ⅱ）当t=﹣5时，动直线y=t经过点C，不合题意；（Ⅲ）当t＜﹣5时，点D在C下方，∠PCQ＜∠DCQ＜90°．‎ ‎【解答】（1）证明：∵A（﹣1，0）在抛物线上，‎ ‎∴a﹣b﹣5=0，‎ ‎∴b=a﹣5，‎ ‎∴抛物线的对称轴为直线x=﹣=，‎ ‎∵0＜a＜5，‎ ‎∴2a＞0，5﹣a＞0，‎ ‎∴＞0，‎ ‎∴此时抛物线的对称轴一定在y轴的右侧；‎ ‎（2）解：①∵A（﹣1，0），B（5，0）在抛物线上，‎ ‎∴，解得，‎ ‎∴二次函数关系式为y=x2﹣4x﹣5，‎ ‎∵y=（x﹣2）2﹣9，‎ ‎∴抛物线的顶点坐标为（2，﹣9），‎ ‎∴当t＞﹣9时，动直线y=t（t为常数）与抛物线交于不同的两点P、Q；‎ ‎②直线y=t交y轴于点D，连接PC、CQ，如图，设点Q的坐标为（m，t）（m＞0），‎ ‎∵P、Q关于直线x=2对称，‎ ‎∴点P的坐标为（﹣m+4，t），‎ ‎（Ⅰ）当t＞﹣5时，点D在点C上方，如图1，‎ ‎∵Q（m，t）在抛物线上，‎ ‎∴t=m2﹣4m﹣5，即t+5=m2﹣4m，‎ ‎∵t＞﹣5，‎ ‎∴m＞4，‎ ‎∴CD=t+5，DQ=m，DP=m﹣4，‎ ‎∵∠PCQ=∠PCD+∠QCD=90°，∠DPC+∠PCD=90°，‎ ‎∴∠QCD=∠DPC，‎ 又∠PDC=∠QDC=90°，‎ ‎∴△QCD∽△CDP，‎ ‎∴=，即=，整理得（t+5）2=m2﹣4m，‎ ‎∴（t+5）2=t+5，解得t1=﹣5（不合，舍去），t2=﹣4；‎ ‎（Ⅱ）当t=﹣5时，动直线y=t经过点C，∠PCQ不能为90°；‎ ‎（Ⅲ）当t＜﹣5时，点D在C下方，如图2，P、Q都在y轴右则，此时∠PCQ＜∠DCQ＜90°．‎ 综上所述，当t=﹣4，∠PCQ=90°．‎