武汉市中考数学试卷含答案

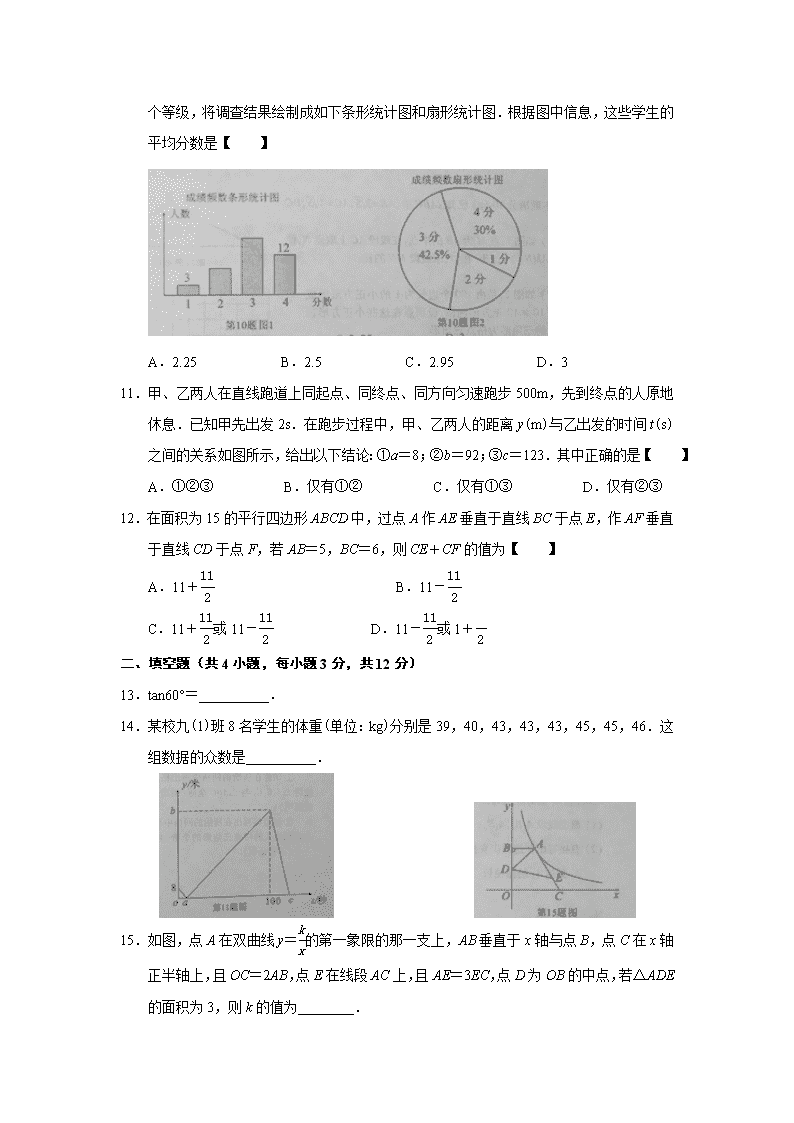
武汉市中考数学试卷含答案

‎2012武汉市中考数学试题 一、 选择题（共12小题，每小题3分，共36分）‎ ‎1．在2.5，－2.5，0，3这四个数中，最小的数是【 】‎ A．2.5 B．－‎2.5 C．0 D．3‎ ‎2．若在实数范围内有意义，则x的取值范围是【 】‎ A．x＜3 B．x≤‎3 C．x＞3 D．≥3‎ ‎3．在数轴上表示不等式x－1＜0的解集，正确的是【 】‎ ‎4．从标号分别为1，2，3，4，5的5张卡片中，随机抽取1张．下列事件中，必然事件是【 】‎ A．标号小于6 B．标号大于‎6 C．标号是奇数 D．标号是3‎ ‎5．若x1、x2是一元二次方程x2－3x＋2＝0的两根，则x1＋x2的值是【 】‎ A．－2 B．‎2 C．3 D．1‎ ‎6．某校2012年在校初中生的人数约为23万．数230000用科学计数法表示为【 】‎ A．23×104 B．2.3×‎105 C．0.23×103 D．0.023×106‎ ‎7．如图，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在边BC的点F处．若AE＝5，BF＝3，则CD的长是【 】‎ A．7 B．‎8 C．9 D．10‎ ‎8．如图，是由4个相同小正方体组合而成的几何体，它的左视图是【 】‎ ‎9．一列数a1，a2，a3，…，其中a1＝，an＝(n为不小于2的整数)，则a4＝【 】‎ A． B． C． D． ‎10．‎ 对某校八年级随机抽取若干名学生进行体能测试，成绩记为1分，2分，3分，4分共4个等级，将调查结果绘制成如下条形统计图和扇形统计图．根据图中信息，这些学生的平均分数是【 】‎ ‎ A．2.25 B．‎2.5 C．2.95 D．3‎ ‎11．甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步‎500m，先到终点的人原地休息．已知甲先出发2s．在跑步过程中，甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示，给出以下结论：①a＝8；②b＝92；③c＝123．其中正确的是【 】‎ A．①②③ B．仅有①② C．仅有①③ D．仅有②③‎ ‎12．在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F，若AB＝5，BC＝6，则CE＋CF的值为【 】‎ A．11＋ B．11－ C．11＋或11－ D．11－或1＋ 二、填空题（共4小题，每小题3分，共12分）‎ ‎13．tan60°＝__________．‎ ‎14．某校九(1)班8名学生的体重(单位：kg)分别是39，40，43，43，43，45，45，46．这组数据的众数是__________．‎ ‎ ‎ ‎15．如图，点A在双曲线y＝的第一象限的那一支上，AB垂直于x轴与点B，点C在x轴正半轴上，且OC＝2AB，点E在线段AC上，且AE＝3EC，点D为OB的中点，若△ADE的面积为3，则k的值为________．‎ ‎16．在平面直角坐标系中，点A的坐标为(3，0)，点B为y轴正半轴上的一点，点C是第一象限内一点，且AC＝2．设tan∠BOC＝m，则m的取值范围是__________．‎ 三、解答题（共9小题，共72分）‎ ‎17．(6分)解方程＝．‎ ‎18．(6分)在平面直角坐标系中，直线y＝kx＋3经过点(－1，1)，求不等式kx＋3＜0的解集．‎ ‎19．(6分)如图CE＝CB，CD＝CA，∠DCA＝∠ECB，求证：DE＝AB．‎ ‎20．(7分)一个口袋中有4个相同的小球，分别与写有字母A、B、C、D，随机地抽出一个小球后放回，再随机地抽出一个小球．‎ ‎(1)使用列表法或树形法中的一种，列举出两次抽出的球上字母的所有可能结果；‎ ‎(2)求两次抽出的球上字母相同的概率．‎ ‎21．(7分)如图，在平面直角坐标系中，点A、B的坐标分别为(－1，3)、(－4，1)，先将线段AB沿一确定方向平移得到线段A1B1，点A的对应点为A1，点B1的坐标为(0，2)，在将线段A1B1绕远点O顺时针旋转90°得到线段A2B2，点A1的对应点为点A2．‎ ‎(1)画出线段A1B1、A2B2；‎ ‎(2)直接写出在这两次变换过程中，点A经过A1到达A2的路径长．‎ ‎22．(8分)在锐角△ABC中，BC＝4，sinA＝．‎ ‎(1)如图1，求△ABC外接圆的直径；‎ ‎(2)如图2，点I为△ABC的内心，BA＝BC，求AI的长？‎ ‎23．(10分)如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE，ED，DB组成，已知河底ED是水平的，ED＝‎16m，AE＝‎8m，抛物线的顶点C到ED的距离是‎11m，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系．‎ ‎(1)求抛物线的解析式；‎ ‎(2)已知从某时刻开始的40h内，水面与河底ED的距离h(单位：m)随时间t(单位：h)的变化满足函数关系h＝－(t－19)2＋8(0≤t≤40)且当水面到顶点C的距离不大于‎5m时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？‎ ‎24．(10分)已知△ABC中，AB＝2，AC＝4，BC＝6．‎ ‎(1)如图1，点M为AB的中点，在线段AC上取点M，使△AMN与△ABC相似，求线段MN的长；‎ ‎(2)如图2，是由100个边长为1的小正方形组成的10×10的正方形网格，设顶点在这些小正方形顶点的三角形为格点三角形．‎ ‎①请你在所给的网格中画出格点△A1B‎1C1与△ABC全等(画出一个即可，不需证明)；‎ ‎②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数，并画出其中一个(不需证明)．‎ ‎25．(12分)如图1，点A为抛物线C1：y＝x2－2的顶点，点B的坐标为(1，0)，直线AB交抛物线C1于另一点C．‎ ‎(1)求点C的坐标；‎ ‎(2)如图1，平行于y轴的直线x＝3交直线AB于点D，交抛物线C1于点E，平行于y轴的直线x＝a交直线AB于F，交抛物线C1于G，若FG：DE＝4∶3，求a的值；‎ ‎(3)如图2，将抛物线C1向下平移m(m＞0)个单位得到抛物线C2，且抛物线C2的顶点为点P，交x轴于点M，交射线BC于点N，NQ⊥x轴于点Q，当NP平分∠MNQ时，求m的值．‎ 参考答案 一、选择题 1． B    2．D    3．B    4．A    5．C   6．B   7．C   8．D   9．A   10． C   11．A    12．D 详解： 3．根式有意义，则x－3≥0 7．EF＝AE＝5 在△BEF中  ∠B＝90°  BF＝3  EF＝5 所以根据勾股定理 BE＝√(5︿2－3︿2)＝4 所以CD＝AE＋EB＝5＋4＝9 10．得4分有12人占30% 则得1分有3人占30%/4＝7．5% 所以得2分有100%－30%－42．5%－7．5%＝20% 所以平均分为4X30%＋3X42．5%＋2X20%＋1X7．5%＝2．95 11．乙出发时甲行了2秒，相距‎8m，所以甲的速度为8/2＝‎4m/S 100秒后乙开始休息．所以乙的速度是500/100＝‎5m/S a秒后甲乙相遇 所以a＝8/(5－4)＝8秒  那么①正确 100秒后乙到达终点，甲走了，4X(100＋2)＝‎408米 所以b＝500－408＝‎92米  那么②正确 甲走到终点一共需耗时500/4＝125秒 所以c＝125－2＝123秒    那么③正确 终上所述选A 二、填空题 ‎ ‎13．√3    14．43   15．k＝16/3   16．m≥(√5)/2 三、解答题 17．解：去分母可得6x＝x＋5 所以x＝1 经检验x＝1确为方程的跟 所以x＝1 18．解：将(－1，1)代入y＝kx＋3得1＝－k＋3 所以k＝2 所以2x＋3＜0 解得 x＜－3/2 19．证明：∠DCA＝∠ECB 所以：∠DCE＝∠ACB 又CD＝CA  CE＝CB 所以：△CDE≌△CAB 所以：DE＝AB 20．解 (1)第一次A(A B C D)  B(A B C D)    第二次C(A B C D)  D(A B C D)‎ ‎(2)由树形图可以看出两次字母相同的概率为4/16＝1/4‎