2011年浙江省台州市中考数学试题

2011年浙江省台州市中考数学试题

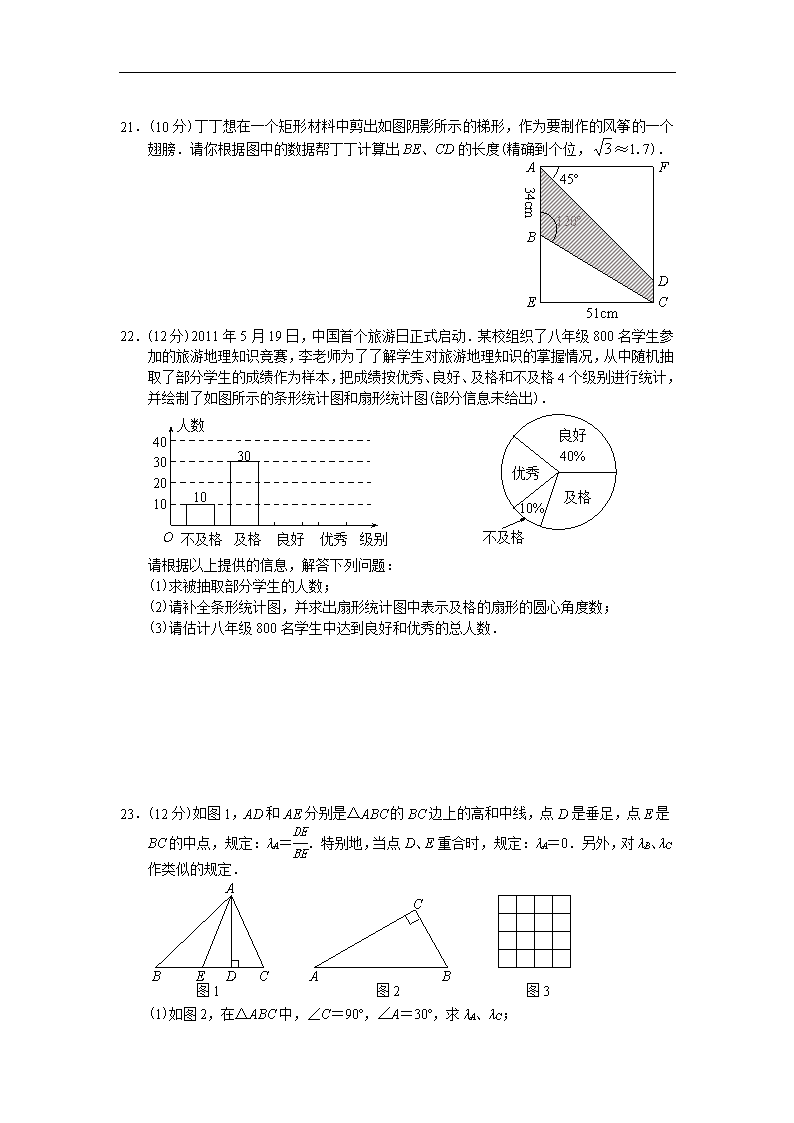
‎2011年浙江省台州市中考数学试题 一、选择题（本题有10小题，每小题4分，满分40分）‎ ‎1．在、0、1、－2这四个数中，最小的数是【 】‎ A． B．‎0 C．1 D．－2‎ ‎2．下列四个几何体中，主视图是三角形的是【 】‎ A．‎ B．‎ C．‎ D．‎ ‎3．要反映台州市某一周每天的最高气温的变化趋势，宜采用【 】‎ A．条形统计图 B．扇形统计图 C．折线统计图 D．频数分布统计图 ‎4．计算(a3)2的结果是【 】‎ A．‎3a2 B．‎2a3 C．a5 D．a6‎ ‎5．若两个相似三角形的面积之比为1∶4，则它们的周长之比为【 】‎ A．1∶2 B．1∶‎4 C．1∶5 D．1∶16‎ ‎6．不等式组的解集是【 】‎ A．x≥3 B．x≤‎6 C．3≤x≤6 D．x≥6‎ A B C D ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎7．在梯形ABCD中，AD∥BC，∠ABC＝90º，对角线AC、BD相交于点O．下列条件中，不能判断对角线互相垂直的是【 】‎ A．∠1＝∠2 B．∠1＝∠3‎ C．∠2＝∠3 D．OB2＋OC2＝BC2‎ A B C D ‎8．如图是一个组合烟花的横截面，其中16个圆的半径相同，点A、B、C、D分别是四个角上的圆的圆心，且四边形ABCD为正方形．若圆的半径为r，组合烟花的高为h，则组合烟花侧面包装纸的面积至少需要(接缝面积不计)【 】‎ A． B．‎ C． D．‎ ‎9．如图，双曲线y＝与直线y＝kx＋b交于点M、N，并且点M的坐标为(1，3)，点N的M N O x y ‎1‎ ‎3‎ ‎－1‎ 纵坐标为－1．根据图象信息可得关于x的方程＝kx＋b的解为【 】‎ O Q P l A．－3，1 B．－3，3‎ C．－1，1 D．－1，3‎ ‎10．如图，⊙O的半径为2，点O到直线l的距离为3，点P是直线l 上的一个动点，PQ切⊙O于点Q，则PQ的最小值为【 】‎ A． B． C．3 D．2‎ 二、填空题（本题有6小题，每小题5分，满分30分）‎ ‎11．若二次根式有意义，则x的取值范围是 ．‎ ‎12．袋子中装有2个黑球和3个白球，这些球的形状、大小、质地等完全相同．随机地从袋子中摸出一个白球的概率是 ．‎ A B C D E F G B1‎ ‎13．因式分解：a2＋‎2a＋1＝ ．‎ ‎14．点D、E分别在等边△ABC的边AB、BC上，将△BDE沿直线DE翻折，使点B落在B1处，DB1、EB1分别交边AC于点F、G．若∠ADF＝80º，则∠CGE＝ ．‎ A B C D O O1‎ O2‎ M ‎15．如果点P(x，y)的坐标满足x＋y＝xy，那么称点P为和谐点．‎ 请写出一个和谐点的坐标： ．‎ ‎16．如图，CD是⊙O的直径，弦AB⊥CD，垂足为点M，AB＝20，分别以CM、DM为直径作两个大小不同的⊙O1和⊙O2，则图中阴影部分的面积为 (结果保留)．‎ 三、解答题（本题有8小题，满分80分）‎ ‎17．(8分)计算：．‎ ‎18．(8分)解方程：．‎ A B C D E F G H ‎19．(8分)如图，分别延长□ABCD的边BA、DC到点E、H，使得AE＝AB，CH＝CD，连接EH，分别交AD、BC于点F、G．‎ 求证：△AEF≌△CHG．‎ ‎20．(8分)毕业在即，九年级某班为纪念师生情谊，班委决定花800元班费买两种不同单价的留念册，分别给50位同学和10位任课教师每人一本作纪念，其中送给任课教师的留念册单价比给同学的单价多8元．请问这两种不同留念册的单价分别是多少？‎ A B E C D F ‎51cm ‎120º ‎34cm ‎45º ‎21．(10分)丁丁想在一个矩形材料中剪出如图阴影所示的梯形，作为要制作的风筝的一个翅膀．请你根据图中的数据帮丁丁计算出BE、CD的长度(精确到个位，≈1.7)．‎ ‎22．(12分)‎2011年5月19日，中国首个旅游日正式启动．某校组织了八年级800名学生参加的旅游地理知识竞赛，李老师为了了解学生对旅游地理知识的掌握情况，从中随机抽取了部分学生的成绩作为样本，把成绩按优秀、良好、及格和不及格4个级别进行统计，并绘制了如图所示的条形统计图和扇形统计图(部分信息未给出)．‎ O 不及格 及格 良好 优秀 级别 人数 ‎40‎ ‎30‎ ‎10‎ ‎20‎ ‎30‎ ‎10‎ ‎10%‎ 优秀 良好 ‎40%‎ 及格 不及格 请根据以上提供的信息，解答下列问题：‎ ‎(1)求被抽取部分学生的人数；‎ ‎(2)请补全条形统计图，并求出扇形统计图中表示及格的扇形的圆心角度数；‎ ‎(3)请估计八年级800名学生中达到良好和优秀的总人数．‎ ‎23．(12分)如图1，AD和AE分别是△ABC的BC边上的高和中线，点D是垂足，点E是BC的中点，规定：λA＝．特别地，当点D、E重合时，规定：λA＝0．另外，对λB、λC作类似的规定．‎ A B E D C A B C 图1‎ 图2‎ 图3‎ ‎(1)如图2，在△ABC中，∠C＝90º，∠A＝30º，求λA、λC；‎ ‎(2)在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点(格点即每个小正方形的顶点)上，且λA＝2，面积也为2；‎ ‎(3)判断下列三个命题的真假(真命题打“P”，假命题打“×”)：‎ ‎①若△ABC中λA＜1，则△ABC为锐角三角形；【 】‎ ‎②若△ABC中λA＝1，则△ABC为锐角三角形；【 】‎ ‎③若△ABC中λA＞1，则△ABC为锐角三角形．【 】‎ ‎24．(14分)已知抛物线y＝a(x－m)2＋n与y轴交于点A，它的顶点为点B，点A、B关于原点O的对称点分别为C、D．若A、B、C、D中任何三点都不在一直线上，则称四边形ABCD为抛物线的伴随四边形，直线AB为抛物线的伴随直线．‎ ‎(1)如图1，求抛物线y＝(x－2)2＋1的伴随直线的解析式．‎ ‎(2)如图2，若抛物线y＝a(x－m)2＋n(m＞0)的伴随直线是y＝x－3，伴随四边形的面积为12，求此抛物线的解析式．‎ ‎(3)如图3，若抛物线y＝a(x－m)2＋n的伴随直线是y＝－2x＋b(b＞0)，且伴随四边形ABCD是矩形．‎ ‎①用含b的代数式表示m、n的值；‎ ‎②在抛物线的对称轴上是否存在点P，使得△PBD是一个等腰三角形？若存在，请直接写出点P的坐标(用含b的代数式表示)，若不存在，请说明理由．‎ A B D C O x y y y O O x x 图1‎ 图2‎ 图3‎