2009年山东省枣庄市中等学校招生考试数学试题及答案

2009年山东省枣庄市中等学校招生考试数学试题及答案

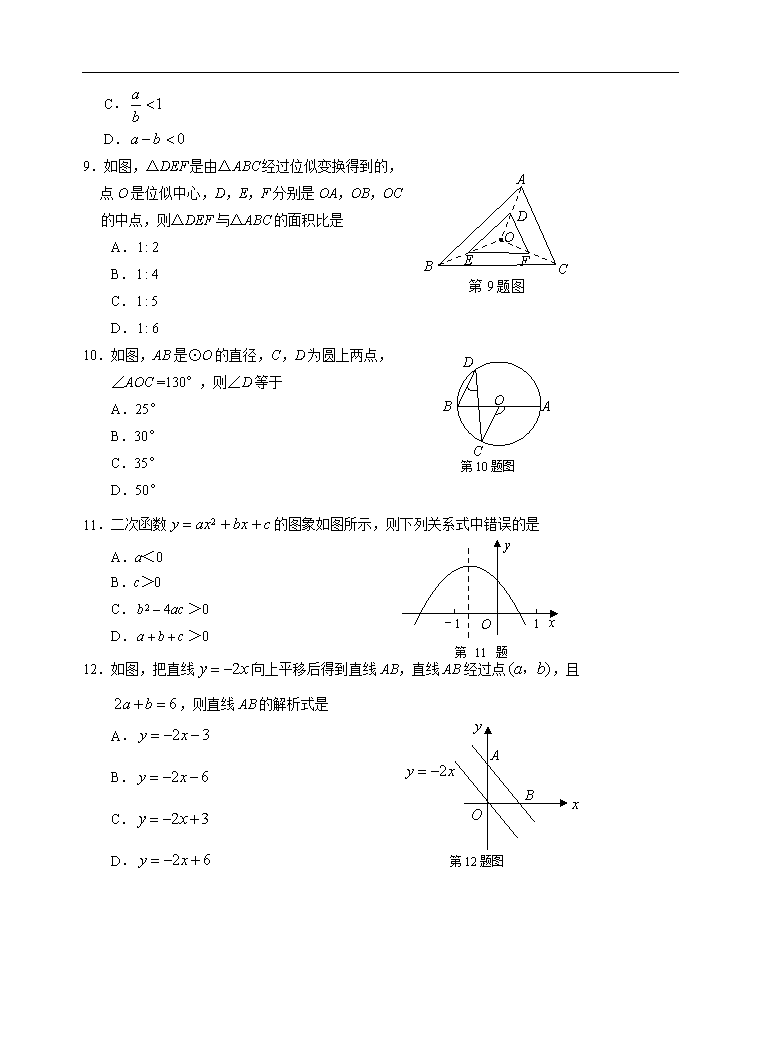
绝密☆启用前 试卷类型：A 枣庄市二○○九年全市高中段招生统一考试 数 学 ‎ 注意事项：‎ ‎ 1．本试题分第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷4页为选择题，36分；第Ⅱ卷8页为非选择题，84分；全卷共12页，满分120分．考试时间为120分钟．‎ ‎ 2．答Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目和试卷类型涂写在答题卡上，并在本页正上方空白处写上姓名和准考证号．考试结束，试题和答题卡一并收回．‎ ‎3．第Ⅰ卷每小题选出答案后，必须用2B铅笔把答题卡上对应题目的答案标号(ABCD)涂黑．如需改动，先用橡皮擦干净，再改涂其它答案．‎ ‎ ‎ 第Ⅰ卷 (选择题 共36分)‎ 一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得３分，选错、不选或选出的答案超过一个均记零分．‎ ‎ 1．－的相反数是 A．2 B． ‎ C． D．‎ ‎2．若m+n=3，则的值为 A．12 B．‎ C．3 D．0‎ ‎3．下列函数中，自变量x的取值范围是的函数是 A．‎ B．‎ C．‎ D．‎ ‎4．请你观察下面的四个图形，它们体现了中华民族的传统文化．‎ 第4题图 对称现象无处不在，其中可以看作是轴对称图形的有 A．4个 B．3个 C．2个 D．1个 cCC aCC bCC ‎2CC ‎1CC 第5题图 ‎5．如图，直线a，b被直线c所截，下列说法正确的是 A．当时，‎ B．当时，‎ C．当时，‎ D．当时，‎ 第6题图 ‎28‎ ‎30‎ ‎31‎ ‎32‎ ‎34‎ ‎37‎ ‎4‎ ‎6‎ ‎5‎ 用水量/吨 ‎1‎ ‎2‎ ‎3‎ 日期/日 ‎0‎ ‎6．某住宅小区六月1日至6日每天用水量变化情况如折线图所示，那么这6天的平均用水量是 A．30吨 B．31吨 C．32吨 D．33吨 第7题图 ‎7．如图，骰子是一个质量均匀的小正方体，它的六个面上分别刻有1~6 个点．小明仔细观察骰子，发现任意相对两面的点数和都相等．这枚骰子向上的一面的点数是5，它的对面的点数是 ‎ A．1‎ B．2‎ C．3‎ D．6‎ ‎8．实数a，b在数轴上的对应点如图所示，则下列不等式中错误的是 A．‎ a b ‎0‎ 第8题图 B．‎ C．‎ D．‎ C A BA DA OA EA FA 第9题图 ‎9．如图，△DEF是由△ABC经过位似变换得到的，‎ 点O是位似中心，D，E，F分别是OA，OB，OC 的中点，则△DEF与△ABC的面积比是 A．‎ B．‎ C．‎ D．‎ D B O A C 第10题图 ‎10．如图，AB是⊙O的直径，C，D为圆上两点，‎ ‎∠AOC =130°，则∠D等于 A．25°‎ B．30°‎ C．35°‎ D．50°‎ 第11题图 ‎ y x O ‎1‎ ‎－1‎ ‎11．二次函数的图象如图所示，则下列关系式中错误的是 A．a＜0 ‎ B．c＞0‎ C．＞0‎ D．＞0‎ ‎12．如图，把直线向上平移后得到直线AB，直线AB经过点，且 ‎，则直线AB的解析式是 第12题图 B A A．‎ B．‎ C．‎ D．‎ 绝密☆启用前 试卷类型：A 二○○九年中等学校招生考试 数 学 第Ⅱ卷 (非选择题 共84分)‎ 注意事项：‎ ‎ 1．第Ⅱ卷共8页，用钢笔或圆珠笔(蓝色或黑色)直接写在试卷上．‎ ‎ 2．答卷前将密封线内的项目填写清楚．‎ 得分 评卷人 二、填空题：本大题共6小题，共24分．只要求填写最后结果，每小题填对得4分． ‎ A B C D O ‎13．布袋中装有1个红球，2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，摸出的球是白球的概率是 ．‎ 第14题图 ‎14．如图，将一副三角板叠放在一起，使直角顶点 重合于O点，则 ．‎ A B O 第16题图 ‎15．a、b为实数，且ab=1，设P=，Q=，则P Q（填“＞”、“＜”或“＝”）．‎ ‎16．如图，直线与轴、轴分别交于、两点，把绕点A顺时针旋转90°后得到，则点的坐标是 ．‎ D C B E A 第17题图 ‎17．如图，在菱形ABCD中，DE⊥AB于E，DE=‎6cm，，则菱形ABCD的面积是__________．‎ ‎18．a是不为1的有理数，我们把称为a的差倒数 ‎．如：2的差倒数是，的差倒数是．已知，是的差倒数，是的差倒数，是的差倒数，…，依此类推，则 ．‎ 得分 评卷人 三、解答题：本大题共7小题，共60分．解答时，要写出必要的文字说明、证明过程或演算步骤． ‎ ‎19．(本题满分8分)‎ ‎ 如图，方格纸中的每个小正方形的边长均为1．‎ ‎（1）观察图①、②中所画的“L”型图形，然后各补画一个小正方形，使图①中所成的图形是轴对称图形，图②中所成的图形是中心对称图形；‎ ‎（第19题图①） ‎ ‎（第19题图②） ‎ ‎（2）补画后，图①、②中的图形是不是正方体的表面展开图：（填“是”或“不是”）‎ 答：①中的图形 ，②中的图形 ．‎ 得分 评卷人 ‎20．（本题满分8分）‎ 某服装专卖店老板对第一季度男、女服装的销售收入进行统计，并绘制了扇形统计图（如图）．由于三月份开展促销活动，男、女服装的销售收入分别比二月份增长了，，已知第一季度男女服装的销售总收入为20万元．‎ ‎（1）一月份销售收入为 万元，二月份销售收入为 万元，三月份销售收入为 万元；‎ 第20题图 一月份 ‎25%‎ 二月份 ‎30%‎ 三月份 ‎45%‎ ‎（2）二月份男、女服装的销售收入分别是多少万元？‎ 得分 评卷人 ‎21．（本题满分8分）‎ 宽与长的比是的矩形叫黄金矩形．心理测试表明：黄金矩形令人赏心悦目，它给我们以协调，匀称的美感．现将小波同学在数学活动课中，折叠黄金矩形的方法归纳如下（如图所示）：‎ 第一步：作一个正方形ABCD；‎ 第二步：分别取AD，BC的中点M，N，连接MN；‎ 第三步：以N为圆心，ND长为半径画弧，交BC的延长线于E；‎ 第四步：过E作EF⊥AD，交AD的延长线于F．‎ 请你根据以上作法，证明矩形DCEF为黄金矩形．‎ A B C D E F M N 第21题图 得分 评卷人 ‎22．(本题满分８分)‎ ‎ ‎ ‎ 为预防“手足口病”，某校对教室进行“药熏消毒”．已知药物燃烧阶段，室内每立方米空气中的含药量y（mg）与燃烧时间x（分钟）成正比例；燃烧后，y与x成反比例（如图所示）．现测得药物10分钟燃烧完，此时教室内每立方米空气含药量为8 mg．根据以上信息，解答下列问题：‎ ‎（1）求药物燃烧时y与x的函数关系式；‎ ‎（2）求药物燃烧后y与x的函数关系式；‎ 第22题图 O ‎8‎ ‎10‎ x (分钟)‎ y (mg)‎ ‎（3）当每立方米空气中含药量低于1.6 mg时，对人体无毒害作用．那么从消毒开始，经多长时间学生才可以返回教室？‎ 得分 评卷人 ‎23．(本题满分8分)‎ 如图，线段AB与⊙O相切于点C，连结OA，OB，OB交⊙O于点D，已知，．‎ ‎（1）求⊙O的半径；‎ 第23题图 C O A B D ‎（2）求图中阴影部分的面积．‎ 得分 评卷人 ‎24．(本题满分10分)‎ 如图，抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线上求点M，使△MOB的面积是△AOB面积的3倍；‎ ‎（3）连结OA，AB，在x轴下方的抛物线上是否存在点N，使△OBN与△OAB相似？若存在，求出N点的坐标；若不存在，说明理由．‎ y x O A B 第24题图 得分 评卷人 ‎25．(本题满分10分)‎ 如图，在平面直角坐标系中，点C（－3，0），点A、B分别在x轴、y轴的正半轴上，且满足．‎ ‎（1）求点A、点B的坐标；‎ ‎（2）若点P从C点出发，以每秒1个单位的速度沿线段CB由C向B运动，连结AP，设的面积为S，点P的运动时间为t秒，求S与t的函数关系式；‎ ‎（3）在（2）的条件下，是否存在点P，使以点A，B，P为顶点的三角形与相似？若存在，请直接写出点P的坐标；若不存在，请说明理由．‎ 第25题图 绝密☆启用前 二○○九年全市高中段招生统一考试 数学参考答案及评分意见 ‎ 评卷说明：‎ ‎ 1．选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分．‎ ‎ 2．解答题每小题的解答中所对应的分数，是指考生正确解答到该步所应得的累计分数．本答案中每小题只给出一种解法，考生的其他解法，请参照评分意见进行评分．‎ ‎ 3．如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半，若出现较严重的逻辑错误，后续部分不给分．‎ 一、选择题：(本大题共12小题，每小题3分，共36分)‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 C A B A D C B C B A D D 二、填空题：(本大题共6小题，每小题4分，共24分)‎ ‎13． 14． 　 15．= 16．（7，3） 17．60　 18．‎ 三、解答题：(本大题共7小题，共60分)‎ ‎ 19．(本题满分8分)‎ ‎（1）如图（画对一个得3分）‎ ‎（图①－１） ‎ 或 ‎（图①－２） ‎ ‎（图②） ‎ ‎ ‎ ‎（2）图①—1（不是）或图①—2（是），图②（是） ……………………………8分 ‎ 20．(本题满分8分)‎ ‎ （1）5，6，9． ………………………………………………………………………3分 ‎（2）设二月份男、女服装的销售收入分别为万元、万元，根据题意，得 ‎ ………………………………………5分 解之，得 ……………………………………………………………7分 答：二月份男、女服装的销售收入分别为3.5万元、2.5万元． ……………8分 ‎21．(本题满分8分)‎ 证明：在正方形ABCD中，取AB=‎2a，‎ ‎∵ N为BC的中点，‎ ‎∴ ．…………………………………………………………………2分 在中，‎ ‎． ………………………………4分 又∵ ，‎ ‎∴ ．……………………………………………………6分 ‎∴ ．‎ 故矩形DCEF为黄金矩形． …………………………………………………………8分 ‎22．(本题满分8分)‎ ‎（1）设药物燃烧阶段函数解析式为，由题意，得 ‎，．‎ ‎∴此阶段函数解析式为(0≤x＜10)． ………………………………2分 ‎（2）设药物燃烧结束后函数解析式为，由题意，得 ‎，．‎ ‎∴此阶段函数解析式为（x≥10）． ……………………………………5分 ‎（3）当y＜1.6时，得． ……………………………………………………6分 ‎∵，‎ ‎∴，．‎ ‎∴从消毒开始经过50分钟学生才返可回教室． ………………………………8分 ‎23．(本题满分8分)‎ ‎ （1）连结OC，则 ． ……………………………………………………1分 ‎∵OA=OB，‎ ‎∴． ………………………………………2分 在中，．‎ ‎∴ ⊙O的半径为3． …………………………………………………………4分 ‎（2）∵ OC=, ∴ ∠B=30o, ∠COD=60o． ……………………………………5分 ‎∴扇形OCD的面积为 ‎==π． …………………………………7分 阴影部分的面积为 ‎=－=－．…………………………8分 ‎24．(本题满分10分) ‎ ‎ （1）由题意，可设抛物线的解析式为，‎ ‎∵抛物线过原点，‎ ‎∴， ．‎ ‎∴抛物线的解析式为．………………………3分 ‎（2）和所求同底不等高，，‎ ‎∴的高是高的3倍，即M点的纵坐标是． ……………5分 ‎∴，即．‎ 解之，得　，．‎ ‎∴满足条件的点有两个：，． ………………………7分 ‎（3）不存在． …………………………………………………………………………8分 由抛物线的对称性，知，．‎ 若与相似，必有．‎ y x O A B E N A′‎ 设交抛物线的对称轴于点，显然．‎ ‎∴直线的解析式为．‎ 由，得，．‎ ‎∴　．‎ 过作轴，垂足为．在中，，，‎ ‎∴．‎ 又OB=4，‎ ‎∴，，与不相似． ‎ 同理，在对称轴左边的抛物线上也不存在符合条件的点．‎ 所以在该抛物线上不存在点N，使与相似． …………10分 ‎25．(本题满分10分)‎ Q P ‎ （1）∵，‎ ‎∴，.‎ ‎∴，OA=1．…………………1分 点A，点B分别在x轴，y轴的正半轴上，‎ ‎∴A（1，0），B（0，）． ……………2分 ‎（2）由（1），得AC=4，，．‎ ‎　　 ∴．‎ ‎∴△ABC为直角三角形，． …………………………………………4分 设CP=t，过P作PQ⊥CA于Q，由△CPQ∽△CBO，易得PQ=．‎ ‎∴S=‎ ‎==－t（0≤t＜）． …………………………7分 ‎ （说明：不写t的范围不扣分）‎ ‎（3）存在，满足条件的的有两个．‎ ‎， ………………………………………………………………………8分 ‎．…………………………………………………………………10分