- 2022-02-12 发布 |
- 37.5 KB |
- 6页

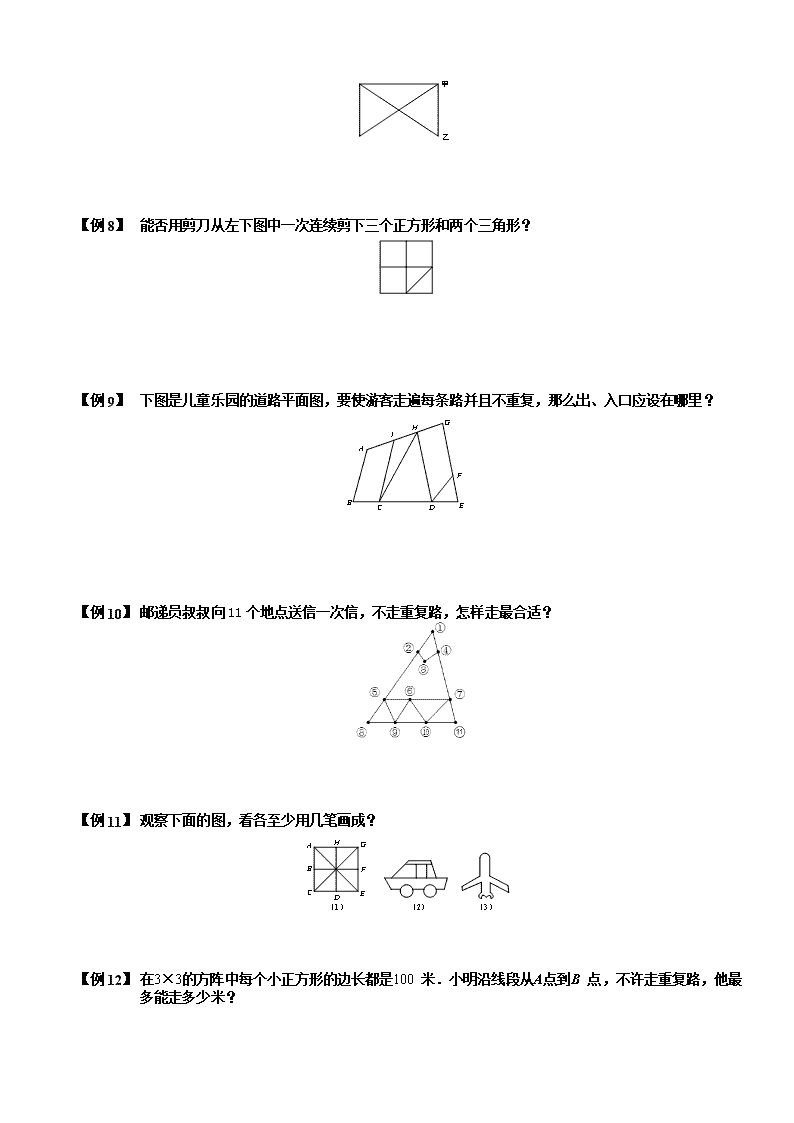
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
小学数学精讲教案4_1_5 奇妙的一笔画 学生版
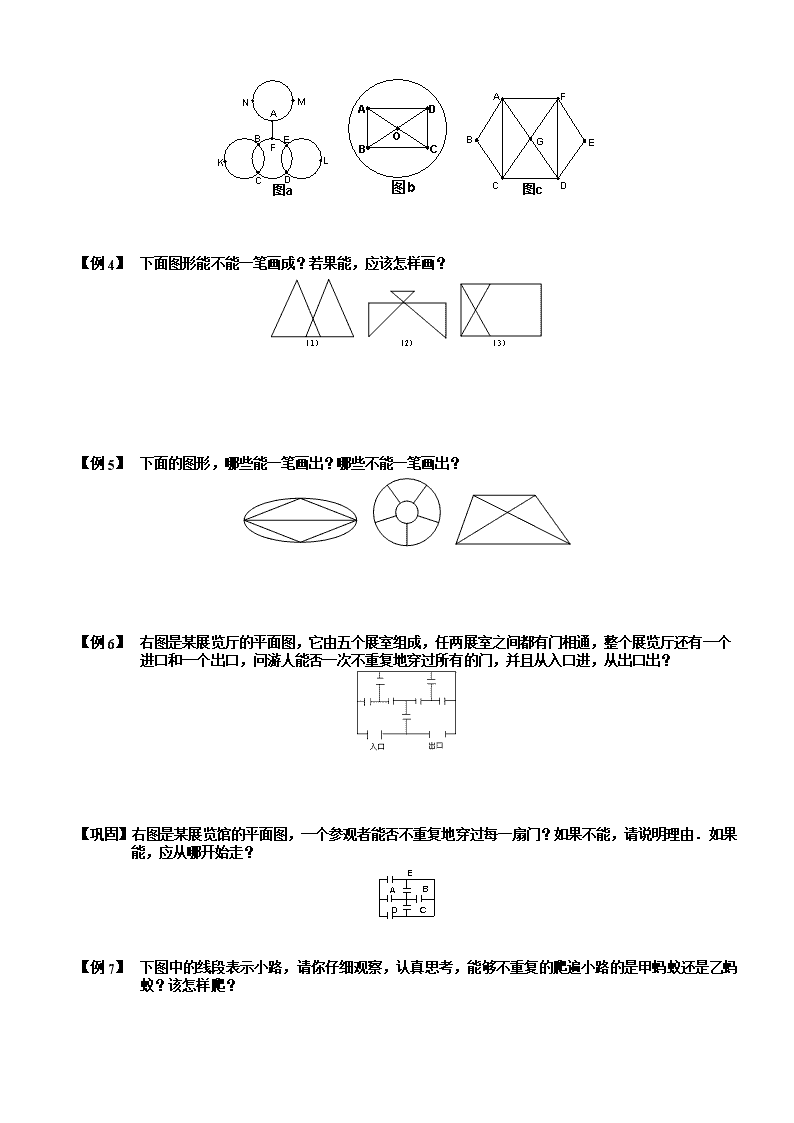
4-1-5.奇妙的一笔画 知识点拨 所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法. 什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏. 我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题: (1)能一笔画出的图形必须是连通的图形; (2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题: 我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n个奇点(n为自然数),那么这个图一定可以用n笔画成. 例题精讲 模块一、判断奇偶点 【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点? 【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务. 【例 3】 判断下列图a、图b、图c能否一笔画. 【例 1】 下面图形能不能一笔画成?若果能,应该怎样画? 【例 2】 下面的图形,哪些能一笔画出?哪些不能一笔画出? 【例 3】 右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出? 【巩固】右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走? 【例 4】 下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬? 【例 1】 能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形? 【例 2】 下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里? 【例 3】 邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适? 【例 4】 观察下面的图,看各至少用几笔画成? 【例 5】 在3×3的方阵中每个小正方形的边长都是100 米.小明沿线段从A点到B 点,不许走重复路,他最多能走多少米? 【例 1】 有个点排成的方阵。如图,请不间断地一笔画出条直线经过每个点,且最后回到起点 【例 2】 一条小虫沿长6分米,宽4分米,高5分米的长方体的棱爬行.如果它只能进不能退,并且同一条棱不能爬两次,那么它最多能爬多少分米? 【巩固】一只木箱的长、宽、高分别为5,4,3厘米(见右图),有一只甲虫从A点出发,沿棱爬行,每条棱不允许重复,则甲虫回到A点时,最多能爬行多少厘米? 模块二、调整奇偶点变一笔画 【例 3】 判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形. 【例 1】 如图是某餐厅的平面图,共有五个小厅,相邻两厅之间有门相通,并且设有入口.请问你能否从入口进入一次不重复地穿过所有的门.如果可以,请指明穿行路线, 如果不能,应关闭哪个门就可以办到? 【例 2】 下图中不能一笔画成,请你在下图中添加最少的线段,将其改成一笔画的图形,并画出路线图. 【例 3】 如图所示,某小区花园的道路为一个长480米,宽200米的长方形;一个边长为260米的菱形和十字交叉的两条道路组成.一天,王大爷A处进入花园,走遍花园的所有道路并从A处离开.如果他每分钟走60米,那么他从进入花园到走出花园最少要用 分. 【例 4】 某城市的交通系统由若干个路口(右图中线段的交点)和街道(右图中的线段)组成,每条街道都连接着两个路口.所有街道都是双向通行的,且每条街道都有一个长度值(标在图中相应的线段处).一名邮递员传送报纸和信件,要从邮局出发经过他所管辖的每一条街道最后返回邮局(每条街道可以经过不止一次).他合理安排路线,可以使得自己走过最短的总长度是 . 【例 1】 18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A和一座半岛D,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功? 【巩固】如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥? 【例 2】 一个邮递员投递信件要走的街道如右图所示,图中的数字表示各条街道的千米数,他从邮局出发, 要走遍各街道,最后回到邮局.怎样走才能使所走的行程最短?全程多少千米? 查看更多