六年级下册数学教案-9 探索多边形中隐藏的规律 ｜冀教版 (1)

六年级下册数学教案-9 探索多边形中隐藏的规律 ｜冀教版 (1)

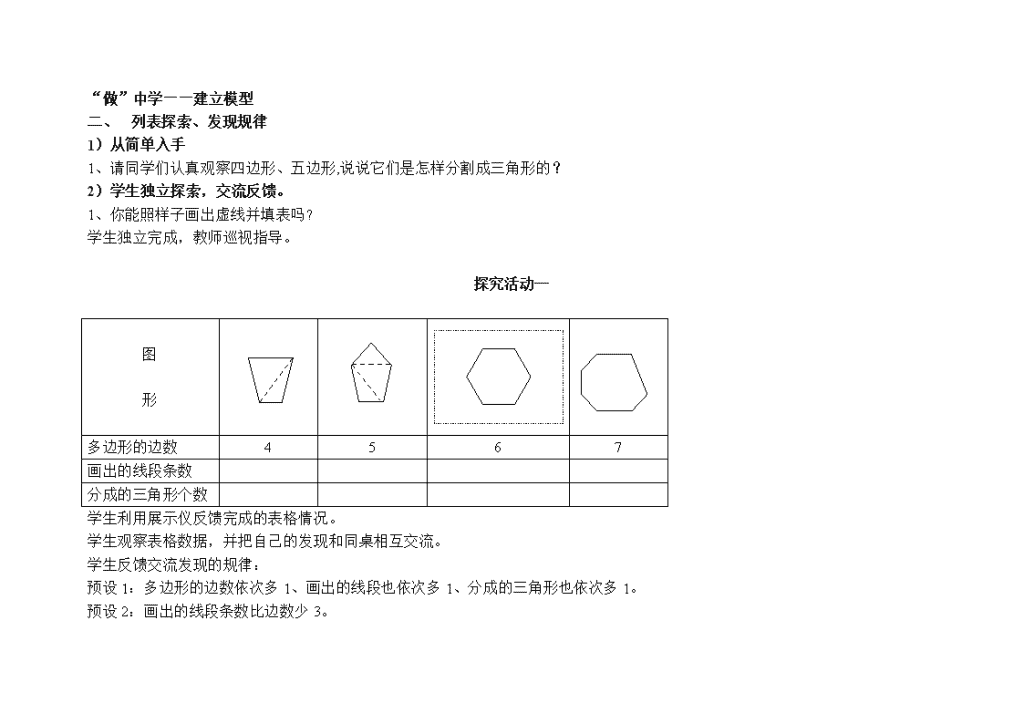
《探索多边形中隐藏的规律》教学设计 教学目标 了解多边形的边数与画出的线段条数、分割成的三角形个数，以及内角和之间隐含的规律，能运用规律解决问题。 通过观察、操作和归纳等数学活动，经历自主探索（合作探索）、发现、总结多边形中隐含规律的过程，感悟探索规律的一般方法。 体会字母表达式的意义，获得探索规律解决问题的成功体验，培养归纳概括和推理能力。 重点 经历由具体的图形发现规律、再把规律扩大到一般、最后总结规律并用字母表达以及应用规律的过程，获得初步的数学建模的活 动经验，体会用字母表达规律的价值。 难点 经历自主探索、合作探索多边形中隐含的数学规律并建立模型的过程，感悟探索规律的一般方法。 教学准备：实物投影仪，多媒体课件，探究活动单 1，探究活动单 2,微课视频。 学情分析 本课是在学生认识了多边形，知道三角形刑内角和等于 180 度，会用字母表示数的基础上进行的。本节课主要是探素多边形 中隐含的规律。教材安排了两个例題：探索多边形的边数与画出的线段条数、分割成的三角形个数之间的规律和探索多边形的内 角和。 教学过程 “抽象”数学问题——建模起点 一、创设情境，激发兴趣 同学们!看,这是什么？（课件出示：北京的水立方） 学生用手比划看到的图案，教师提问看到了哪些平面图形。 引出：在同一平面内，由三条或三条以上的线段首尾顺次连接所组成的封闭图形叫做多边形。 再引出今天的课题：探究多边形中隐藏的规律。（板书：探究多边形中隐藏的规律） 意图：创设情境，贴近生活素材，调动学生的学习积极性。 “做”中学——建立模型 二、 列表探索、发现规律 1）从简单入手 1、请同学们认真观察四边形、五边形,说说它们是怎样分割成三角形的？ 2）学生独立探索，交流反馈。 1、你能照样子画出虚线并填表吗? 学生独立完成，教师巡视指导。 探究活动一 图 形 多边形的边数 4 5 6 7 画出的线段条数 分成的三角形个数 学生利用展示仪反馈完成的表格情况。 学生观察表格数据，并把自己的发现和同桌相互交流。 学生反馈交流发现的规律： 预设 1：多边形的边数依次多 1、画出的线段也依次多 1、分成的三角形也依次多 1。 预设 2：画出的线段条数比边数少 3。 预设 3：多边形的边数-3=画出线段的条数 预设 4：多边形的边数-2=三角形的个数 预设 5：三角形的个数-1=画出线段的条数 3）应用发现，归纳规律 学生应用发现的规律快速填表。 多边形的边数 8 10 50 …… 画出的线段条数 分成的三角形个数 想想：如果是 n 边形呢?可以画出几条线段?分割成几个三角形?指名学生回答并说想法。 4）回顾探索，总结方法 教师提问:回顾我们探索规律的过程，想想今天我们是怎么探索规律的？ 回顾：先是观察四边形、五边形是怎么分成三角形的，照样子画虚线并填表，再通过观察表格的数据发现规律，然后应用规律。 教师小结：嗯，往后探索复杂的规律，我们可以先从简单的入手，然后观察，操作，归纳所发现的规律。接下来我们用这种探索 规律的方法继续来探索多边形的内角和.（板书：观察——操作——归纳） 设计意图：观察四边形、五边形是怎么分成三角形的，照样子画虚线并填表，再通过观察表格的数据发现规律，然后应用规律这 个过程，体验知识的形成过程，培养学生的探究能力，获得探索规律的一般方法，即可以从简单入手，从特殊到一般的方法感悟。 “思”中学——应用模型 三、 方法应用，体验快乐 教师提问：从何入手探索多边形的内角和？ 预设：从四边形入手 1）探索四边形的内角和 请学生猜想四边形的内角和是多少度？ 预设：360° 学生自由畅说自己的想法。 预设 1：长方形的四个角是直角，加起来是 360 度。 此时教师及时表扬学生很会猜想，会从特殊的图形进行猜想。 预设 2: 通过我们刚才的探索知道：一个四边形可以分成两个三角形，一个三角形的内角和是 180°，两个三角形的内角和就是 360° 提问：四边形的 4 个内角和和两个三角形的 6 个内角之和有什么联系？ 教师请学生上讲台给大家讲解一下。 得到结论：四边形的内角和是 2×180° 过渡：转化真是学习数学的好方法！现在请同学们取出探究活动二，两人一组。类比四边形内角和的探究方法继续探索多边形内 角和。 探究活动 2：小组合作，类比探索多边形的内角和 图形 …… n 边形 多边形的边数 4 5 6 7 n 分成的三角形个数 2 多边形的内角和 2×180°=360° 小组讨论：1、多边形的内角和和各三角形的内角和有何关系？ 2、多边形的内角和和边数有何关系？ 3、完成表格。 让学生观察表中的数据，说说发现了什么？ 预设 1：多一条边，内角和就多 180° 预设 2：分成了几个三角形，多边形的内角和就有几个 180° 问题:1：你能用一个式子表示多边形内角和的计算方法吗？ 问题 2：如果是 n 边形呢?你能用 n 表示它的内角和吗? 预设：（n－２）×180°（板书：多边形的内角和＝（n－２）×180° 请同桌两人之间相互提问：一人任意说一个多边形，另一人说出计算内角和的算式。 设计意图：学生通过对规律探索方法的再应用，获得探索规律的成功体验，增强了学习数学的信心。 四、规律应用，体验价值 （1）你能算出八卦图的内角和吗？（课件出示：浙江金华兰溪诸葛八卦村） （2）小明在上完这节课后，当天晚上在自己的数学日记里写道：我有一个愿望，想在 2160 年设计一个多边形，让它的内角和是 2160°，小明能做到吗？ 说说你的理由。 教师表扬：通过刚才同学们的表现，老师发现我们班的同学真是解决问题的小能手。 意图：与探究多边形的内角和的过程相呼应，以及多边形内角和公式的基础运用，让每个学生都能获得必需的数学知识。也体现 了探索规律的价值实用性。 拓展补充 (多媒体播放微课)从多边形的内部取一点将多边形分割成若干个三角形进行多边形内角和规律的探索。 让学生体验，虽然分的方法不一样，但探究规律的方法是一样的，课后同学们可以试着从多边形的边上取点去画线段继续探索。 五、课堂小结，畅所欲言 回顾探索和发现规律的过程，说说你有什么体会或收获？ 预设：在数学学习中，我们能多观察，多思考，你就会发现原来数学中隐藏这么多有趣的规律。 六、总结全课，寄托希望 教师: 同学们成功地完成了此次探索之旅。在我们的生活,学习中里还有很多有趣的规律等着大家去探索。只要你仔细观察,善于思 考,勇于探索，坚持不懈，一定会有所发现的。 七、板书设计： 探索多边形隐藏的规律 n 边形 画出线段的条数: n-3 分成的三角形个数: n-2 内角和: (n - 2) ×180° 从简单的入手 观察 操作 归纳